Introduction to Negative Numbers Chapter Notes | Mathematics Class 5 ICSE PDF Download
Introduction
Imagine standing at the edge of a vast number line stretching infinitely in both directions, where numbers tell stories of direction, depth, and change. The chapter "Introduction to Negative Numbers" opens the door to a fascinating world beyond the familiar counting numbers, introducing integers—a family that includes positive numbers, zero, and their mysterious counterparts, negative numbers. These numbers help us describe real-life situations, like temperatures below zero, depths below sea level, or even losses in a game. By exploring integers, we learn to navigate this number line, compare values, and perform operations that make sense of the world around us. Get ready to dive into a mathematical adventure that expands how we think about numbers!
Natural Numbers and Whole Numbers
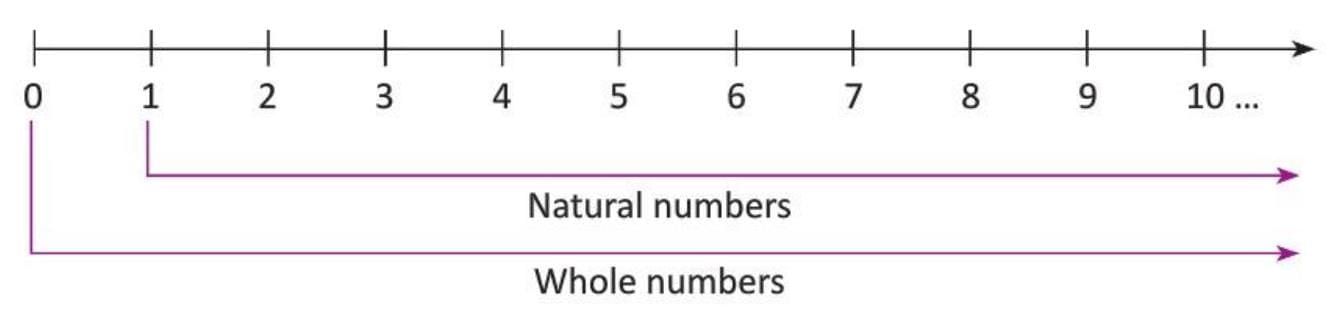
- Natural numbers are the counting numbers we use daily, starting from 1 (e.g., 1, 2, 3, 4, …).
- They begin with 1, the smallest natural number, and each number is found by adding 1 to the previous one.
- Whole numbers include all natural numbers plus zero (e.g., 0, 1, 2, 3, 4, …).
- Zero is the smallest whole number, and there is no largest natural or whole number since they go on infinitely.
- These numbers can be shown on a straight line, called a number line, with equal spaces between them.
- Subtraction works when a smaller number is subtracted from a larger one, but subtracting a larger number from a smaller one (e.g., 3 - 4) requires a new number system called integers.
- Example: If we try to subtract 4 from 3 (i.e., 3 - 4), we need a number such that 4 + ? = 3. Since no whole number satisfies this, we extend to integers to find the answer.
Integers
- Integers include all counting numbers (1, 2, 3, …), zero, and their negatives (…, -3, -2, -1).
- Examples of integers are …, -4, -3, -2, -1, 0, 1, 2, 3, 4, …
- Negative numbers (e.g., -1, -2, -3) are less than zero, while positive numbers (e.g., 1, 2, 3) are greater than zero.
- Zero is an integer but is neither positive nor negative.
- Example: The numbers -4, -3, -2, -1, 0, 1, 2, 3, 4 are all integers, showing the full range from negative to positive numbers.
Representation of Integers on a Number Line
- A number line is a straight line with integers marked at equal distances.
- Steps to draw a number line:
- Draw a horizontal line and mark a point as 0 in the center.
- Mark points to the right of 0 at equal intervals, labeling them as 1, 2, 3, 4, … (positive integers).
- Mark points to the left of 0 at equal intervals, labeling them as -1, -2, -3, -4, … (negative integers).

- Positive and negative pairs (e.g., 1 and -1, 2 and -2) are equidistant from 0 but in opposite directions.
- Positive integers are to the right of 0, written with or without a '+' sign.
- Negative integers are to the left of 0, written with a '-' sign (e.g., -1 is read as "negative one").
- The greatest negative integer is -1.
- Example: To represent -9, -2, 4, and 7 on a number line, mark -9 and -2 to the left of 0 and 4 and 7 to the right of 0 at equal intervals.

Necessity of Negative Numbers
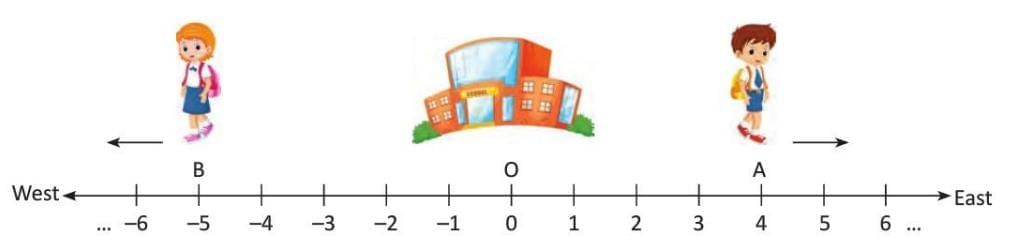
Negative numbers are essential for describing opposites in real life, such as:
- Opposite directions (e.g., east vs. west).
- Height above sea level vs. depth below sea level.
- Temperature above and below 0°C.
- Profits vs. losses in business.
- Rise vs. fall in prices.
- Example: Rohan walks 4 m east from school (marked as +4 m), and Tripti walks 5 m west (-5 m), showing how negative numbers represent opposite directions.
Predecessor and Successor of an Integer
- The predecessor of an integer is the number one less than it (e.g., the predecessor of 2 is 1).
- The successor of an integer is the number one more than it (e.g., the successor of 2 is 3).
- On a number line, the predecessor is the integer to the left, and the successor is to the right.
- Example: For the integer -2, the predecessor is -3 (one step left), and the successor is -1 (one step right).
Comparison of Integers Using a Number Line
- A number line helps compare integers by their position.
- The integer on the right is greater than the one on the left.
- Values increase from left to right and decrease from right to left.
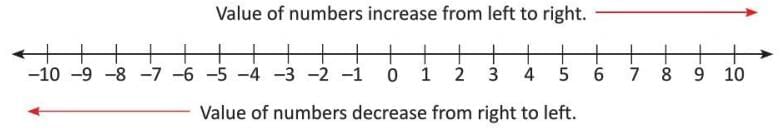
- Key rules:
- Every positive number is greater than every negative number.
- Zero is less than every positive number but greater than every negative number.
- The farther a number is to the right of 0, the greater its value.
- The farther a number is to the left of 0, the smaller its value.
- Example: On a number line, 10 is to the right of 4, so 10 is greater than 4.
Ordering of Integers
Integers can be arranged in ascending (smallest to greatest) or descending (greatest to smallest) order using a number line.
Steps to arrange integers:
- Draw a number line and mark the given integers.
- For ascending order, list integers from left to right.
- For descending order, list integers from right to left.
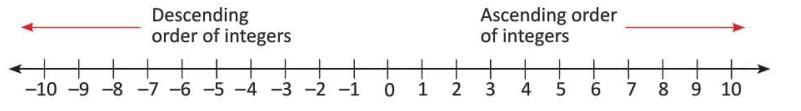
- Example: To arrange 5, -2, 1, -1, and 0:

Ascending order: -2, -1, 0, 1, 5 (left to right).
Descending order: 5, 1, 0, -1, -2 (right to left).
Addition of Integers on a Number Line
Addition of Two Positive Integers
- Move to the right of 0 to the first integer, then move further right by the second integer to find the sum.
- The result is a positive integer.
- Example: To add 4 + 5:
 Move 4 steps right from 0 to 4, then 5 more steps right to reach 9. So, 4 + 5 = 9.
Move 4 steps right from 0 to 4, then 5 more steps right to reach 9. So, 4 + 5 = 9.
Addition of a Positive and a Negative Integer
- Move to the right of 0 to the positive integer, then move left by the negative integer to find the sum.
- Subtract the smaller number from the larger one, and the result takes the sign of the larger number.
- Example: To add 6 + (-2):
 Move 6 steps right from 0 to 6, then 2 steps left to reach 4. So, 6 + (-2) = 4.
Move 6 steps right from 0 to 6, then 2 steps left to reach 4. So, 6 + (-2) = 4.
Addition of a Negative and a Positive Integer
- Move to the left of 0 to the negative integer, then move right by the positive integer to find the sum.
- Subtract the smaller number from the larger one, and the result takes the sign of the larger number.
- Example: To add -2 + 5:
 Move 2 steps left from 0 to -2, then 5 steps right to reach 3. So, -2 + 5 = 3.
Move 2 steps left from 0 to -2, then 5 steps right to reach 3. So, -2 + 5 = 3.
Addition of Two Negative Integers
- Move to the left of 0 to the first negative integer, then move further left by the second negative integer to find the sum.
- The result is a negative integer.
- Example: To add -4 + (-3):
 Move 4 steps left from 0 to -4, then 3 more steps left to reach -7. So, -4 + (-3) = -7.
Move 4 steps left from 0 to -4, then 3 more steps left to reach -7. So, -4 + (-3) = -7.
Addition of Integers without Using a Number Line
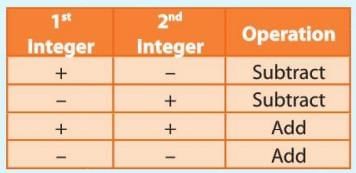
- For integers with the same sign: Add the numbers and keep the same sign.
- For integers with different signs: Ignore the signs, subtract the smaller number from the larger one, and give the result the sign of the larger number.
- If no sign is written before a number, it is positive.
- Example
(a) 5 + 7: Both positive, so 5 + 7 = 12, result is +12.
(b) 12 + (-8): Different signs, 12 - 8 = 4, since 12 is positive, result is +4.
Subtraction of Integers on a Number Line
- Subtraction of Two Positive Integers: Move to the right of 0 to the first integer (subtrahend), then move left by the second integer (minuend) to find the difference.
Example: To subtract 3 - 4: Move 3 steps right from 0 to 3, then 4 steps left to reach -1. So, 3 - 4 = -1.
Move 3 steps right from 0 to 3, then 4 steps left to reach -1. So, 3 - 4 = -1. - Subtraction of a Positive Integer from a Negative Integer: Move to the left of 0 to the negative integer (subtrahend), then move further left by the positive integer (minuend) to find the difference.
Example: To subtract -3 - 4: Move 3 steps left from 0 to -3, then 4 steps further left to reach -7. So, -3 - 4 = -7.
Move 3 steps left from 0 to -3, then 4 steps further left to reach -7. So, -3 - 4 = -7. - Subtraction of a Negative Integer from a Positive Integer: Move to the right of 0 to the positive integer (subtrahend), then move right by the negative integer (minuend) to find the difference. A negative minuend changes to positive (e.g., 4 - (-8) becomes 4 + 8).
Example: To subtract 4 - (-8): Move 4 steps right from 0 to 4, then 8 steps further right to reach 12. So, 4 - (-8) = 12.
Move 4 steps right from 0 to 4, then 8 steps further right to reach 12. So, 4 - (-8) = 12. - Subtraction of a Negative Integer from a Negative Integer: Move to the left of 0 to the negative integer (subtrahend), then move right by the negative integer (minuend) to find the difference.
Example: To subtract -5 - (-3): Move 5 steps left from 0 to -5, then 3 steps right to reach -2. So, -5 - (-3) = -2.
Move 5 steps left from 0 to -5, then 3 steps right to reach -2. So, -5 - (-3) = -2.
Subtraction of Integers without Using a Number Line
Steps for subtraction:
- Keep the sign of the first integer (subtrahend) as it is.
- Change the sign of the second integer (minuend): positive becomes negative, negative becomes positive.
- Follow the rules of addition to find the result.
- Example
(a) 6 - 7: Keep 6, change +7 to -7, so 6 - 7 = 6 + (-7) = -1.
(b) -11 - (-19): Keep -11, change -19 to +19, so -11 - (-19) = -11 + 19 = 8.
|
138 docs|15 tests
|
FAQs on Introduction to Negative Numbers Chapter Notes - Mathematics Class 5 ICSE
| 1. What are natural numbers and whole numbers? |  |
| 2. How are integers represented on a number line? |  |
| 3. Why do we need negative numbers? |  |
| 4. What is the predecessor and successor of an integer? |  |
| 5. How do you add integers without using a number line? |  |















