Addition and Subtraction Chapter Notes | Mathematics for Primary 6 PDF Download
Introduction
Mathematics is like a fun adventure, and addition and subtraction are the trusty tools that help us solve everyday puzzles! Whether it's counting the total number of books in a library or finding out how much money is left after a big purchase, these operations make life easier. In this chapter, we'll dive into the exciting world of adding and subtracting large numbers, discovering how to handle missing digits, estimate results, and create real-life word problems. Get ready to explore these skills step-by-step and become a math wizard!

Addition
Addition means combining two or more numbers, called addends, to find their total, known as the sum.
Steps to add numbers:
- Arrange the numbers in columns based on their place values (ones, tens, hundreds, etc.).
- Start adding from the rightmost column (ones place) and move left to larger place values.
- Write the sum below each column.
Addition of Large Numbers (without carry over)
Add large numbers by aligning them in columns according to place values. Start from the ones place and add each column moving left to tens, hundreds, thousands, etc. No carry over occurs when the sum of digits in a column is less than 10.
Example: Find the sum of 37,241 and 21,356. Write the sum in words.
- Arrange in columns:
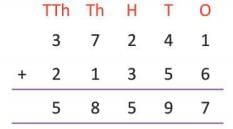
- Add ones: 1 + 6 = 7
- Add tens: 4 + 5 = 9
- Add hundreds: 2 + 3 = 5
- Add thousands: 7 + 1 = 8
- Add ten thousands: 3 + 2 = 5
- Sum: 58,597
- In words: fifty-eight thousand five hundred ninety-seven
Addition of Large Numbers (with carry over)
- When the sum of digits in a column is 10 or more, write the ones digit and carry over the tens digit to the next column. Add the carried-over digit with the digits in the next column. Continue this process for each column moving left.
Example: Find the sum of 42,618 and 37,956. Write the sum in words.
- Arrange in columns and add step-by-step, noting carry overs.
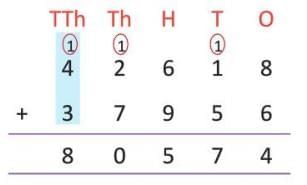
- Ones: 8 + 6 = 14 (write 4, carry 1 to tens)
- Tens: 1 + 1 + 5 = 7 (write 7, no carry)
- Hundreds: 6 + 9 = 15 (write 5, carry 1 to thousands)
- Thousands: 1 + 2 + 7 = 10 (write 0, carry 1 to ten thousands)
- Ten thousands: 1 + 4 + 3 = 8
- Sum: 80,574
- In words: eighty thousand five hundred seventy-four
Finding the Missing Digits
Use place values to find missing digits in addition problems.
Steps to find missing digits:
- Start with the ones column and check the sum.
- If the sum has a specific ones digit, find the number that, when added to the known digit, gives the sum (considering carry overs).
- Move to the next columns (tens, hundreds, etc.), accounting for any carry overs from previous columns.
- Continue until all missing digits are found.
Example: Find the missing digits.
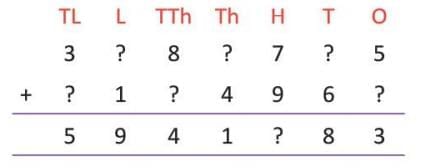
- Ones column: 5 + ? = 13 (since 3 is in the ones place of the sum, and 13 has 3 in ones). So, 13 - 5 = 8. Write 8 in the ones place of the second addend. Carry 1 to tens.
- Tens column: 1 (carry) + ? + 6 = 8. So, ? + 7 = 8, thus ? = 1. Write 1 in the tens place of the first addend.
- Continue for other columns to find all missing digits.
Estimating the Sum
Estimation gives an approximate sum close to the actual sum.
Steps to estimate:
- Round each addend to the nearest 10, 100, 1,000, etc., based on required accuracy.
- Add the rounded numbers to get the estimated sum.
- Compare with the actual sum to check closeness.
Example: In a village, there are 12,645 men, 11,378 women, and 5,798 children. Estimate the total population by rounding to the nearest 100. Check if the estimated population is close to the actual.
- Actual numbers: Men = 12,645, Women = 11,378, Children = 5,798
- Actual sum: 12,645 + 11,378 + 5,798 = 29,821
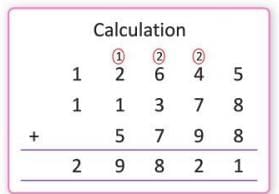
- Round to nearest 100: Men = 12,600, Women = 11,400, Children = 5,800
- Estimated sum: 12,600 + 11,400 + 5,800 = 29,800
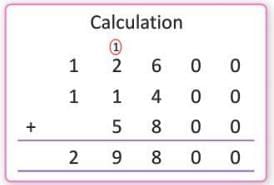
- Check: Actual sum 29,821 rounded to nearest 100 is 29,800, so the estimate is close.
Word Problems on Addition
Word problems involve adding numbers to solve real-life situations.
Steps to solve:
- Identify the numbers to be added from the problem.
- Add the numbers using column addition, handling carry overs if needed.
- Write the final answer with appropriate units (e.g., books, people).
Example: A publisher sold 1,46,750 books in January, 1,52,430 in February, and 1,60,000 in March. How many books were sold in three months?
- Numbers: January = 1,46,750, February = 1,52,430, March = 1,60,000
- Add: 1,46,750 + 1,52,430 + 1,60,000 = 4,59,180
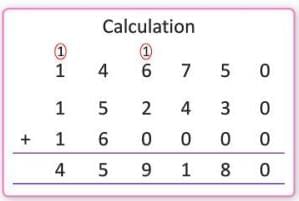
- Answer: The publisher sold 4,59,180 books in three months.
Framing Word Problems on Addition
Create word problems by using given numbers to describe real-life scenarios.
Steps to frame:
- Choose a context (e.g., money, population, items).
- Use the given numbers as quantities in the scenario.
- Form a question asking for the total sum.
Example: Frame two word problems for 51,289 + 21,364.
- Problem 1: Town A has 51,289 people, and Town B has 21,364 people. How many people are in both towns?
- Problem 2: Ronit had ₹51,289 in his account and deposited ₹21,364 more. How much money is in his account now?
Subtraction
Subtraction means taking away one number (subtrahend) from another (minuend) to find the difference. It is the opposite of addition.
Steps to subtract:
- Arrange numbers in columns by place values.
- Subtract from the ones place, moving left to larger place values.
- Write the difference below each column.
Subtraction of Large Numbers (without borrowing)
Subtract large numbers by aligning them in columns by place values. Start from the ones place and subtract each column moving left. No borrowing is needed when the minuend’s digit is larger than or equal to the subtrahend’s digit in each column.
Example: Find the difference between 87,632 and 42,102. Write the difference in words.
- Arrange in columns:
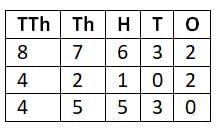
- Subtract ones: 2 - 2 = 0
- Subtract tens: 3 - 0 = 3
- Subtract hundreds: 6 - 1 = 5
- Subtract thousands: 7 - 2 = 5
- Subtract ten thousands: 8 - 4 = 4
- Difference: 45,530
- In words: forty-five thousand five hundred thirty
Subtraction of Large Numbers (with borrowing)
When the minuend’s digit is smaller than the subtrahend’s digit, borrow 1 from the next higher place value. Reduce the higher place value by 1 and add 10 to the current place value. Subtract the digits and continue to the next columns.
Example: Subtract 32,179 from 61,452.
- Arrange in columns and subtract, borrowing when needed.
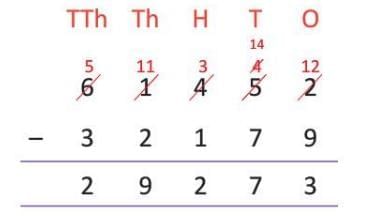
- Ones: 2 - 9 (cannot subtract, borrow 1 from tens, making tens 4, ones 12). 12 - 9 = 3
- Tens: 4 - 7 (borrow 1 from hundreds, making hundreds 4, tens 14). 14 - 7 = 7
- Hundreds: 4 - 1 = 3
- Thousands: 1 - 2 (borrow 1 from ten thousands, making ten thousands 5, thousands 11). 11 - 2 = 9
- Ten thousands: 5 - 3 = 2
- Difference: 29,273
- In words: twenty-nine thousand two hundred seventy-three
Subtraction with Zeros
When subtracting from a number with zeros, borrowing can involve multiple columns.
Steps:
- If the minuend’s digit is 0 or smaller than the subtrahend’s digit, borrow from the next non-zero place value.
- Adjust the place values accordingly (e.g., borrow 1 from thousands, give 10 to hundreds, then to tens, then to ones).
- Subtract column by column.
Example: Subtract 48,256 from 87,002.
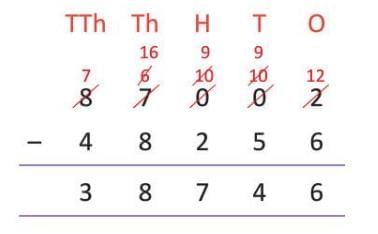
- Ones: 2 - 6 (cannot subtract, borrow from tens, but tens is 0, so borrow from hundreds, but hundreds is 0, so borrow from thousands).
- Borrow 1 from thousands (8 to 7), hundreds becomes 10, tens becomes 9, ones becomes 12.
- Ones: 12 - 6 = 6
- Tens: 9 - 5 = 4
- Hundreds: 9 - 2 = 7
- Thousands: 7 - 8 (borrow from ten thousands, 8 to 7, thousands become 17). 17 - 8 = 9
- Ten thousands: 7 - 4 = 3
- Difference: 38,746
Checking Subtraction through Addition
To check if subtraction is correct, add the difference and the subtrahend. If the sum equals the minuend, the subtraction is correct; if not, it’s incorrect.
Steps to check:
- After subtracting, take the difference and add it to the subtrahend.
- Compare the result with the minuend.
- If they match, the subtraction is correct.
Example: Subtract 4,25,178 from 7,60,085 and check your answer.
- Arrange in columns:
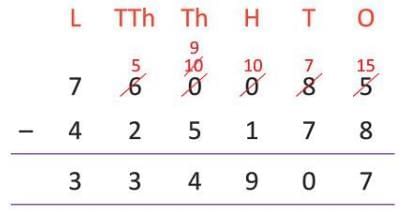
- Difference: 3,34,907
- Check by adding difference and subtrahend:
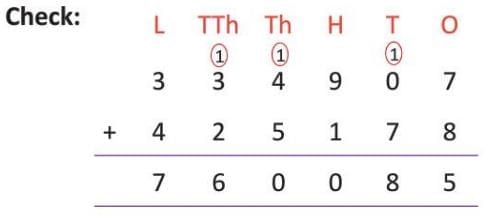
- Sum: 7,60,085 (matches the minuend, so subtraction is correct)
Finding the Missing Digits
Use place values and subtraction formulas: Difference = Minuend - Subtrahend, or Minuend = Difference + Subtrahend, or Subtrahend = Minuend - Difference.
Steps:
- Start with the ones column and use the appropriate formula to find the missing digit.
- Account for borrowing in previous columns if needed.
- Move to the next columns, repeating the process.
Example: Find the missing digits.
- Ones: 5 - ? = 3. So, ? = 5 - 3 = 2. Write 2 in ones of subtrahend.
- Tens: ? - 1 = 1. So, ? = 1 + 1 = 2. Write 2 in tens of minuend.
- Continue for other columns to find all missing digits.
Estimating the Difference
Estimation gives an approximate difference close to the actual difference.
Steps:
- Round the minuend and subtrahend to the nearest 10, 100, 1,000, etc.
- Subtract the rounded numbers to get the estimated difference.
- Compare with the actual difference to check accuracy.
Example: Estimate the difference between 7,45,236 and 4,63,815 by rounding to the nearest 1,000. Check if the estimated difference is correct.
- Actual numbers: Minuend = 7,45,236, Subtrahend = 4,63,815
- Actual difference: 7,45,236 - 4,63,815 = 2,81,421
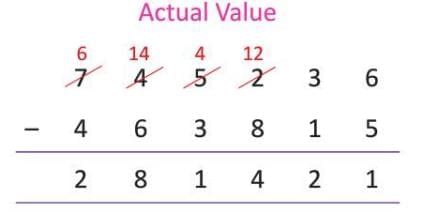
- Round to nearest 1,000: Minuend = 7,45,000, Subtrahend = 4,64,000
- Estimated difference: 7,45,000 - 4,64,000 = 2,81,000
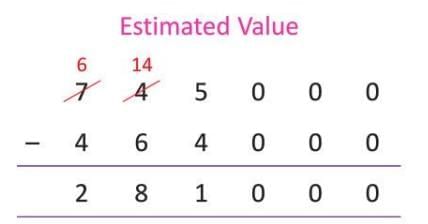
- Check: Actual difference 2,81,421 rounded to nearest 1,000 is 2,81,000, so the estimate is correct.
Word Problems on Subtraction
Word problems involve subtracting numbers to solve real-life situations.
Steps to solve:
- Identify the minuend and subtrahend from the problem.
- Subtract using column subtraction, handling borrowing if needed.
- Write the final answer with appropriate units.
Example: The sum of two numbers is 3,54,370. If one number is 1,82,756, what is the other number?
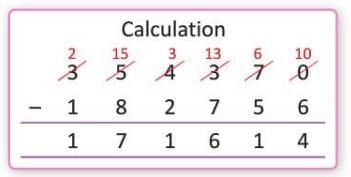
- Sum = 3,54,370, One number = 1,82,756
- Other number = Sum - Given number = 3,54,370 - 1,82,756 = 1,71,614
- Answer: The other number is 1,71,614.
Framing Word Problems on Subtraction
Create word problems by using given numbers in real-life scenarios.
Steps to frame:
- Choose a context (e.g., money, population, items).
- Use the given numbers as the minuend and subtrahend.
- Form a question asking for the difference.
Example: Frame two word problems for 1,50,000 - 75,000.
- Problem 1: Arjun had ₹1,50,000 in his bank account. He withdrew ₹75,000 for an investment. How much money is left in his account?
- Problem 2: Town A had 1,50,000 people. If 75,000 moved to Town B, how many people are left in Town A?
|
147 videos|222 docs|54 tests
|
FAQs on Addition and Subtraction Chapter Notes - Mathematics for Primary 6
| 1. What is the importance of learning addition and subtraction in Class 5? |  |
| 2. How can I help my child practice addition and subtraction at home? |  |
| 3. What are some common strategies for solving addition and subtraction problems? |  |
| 4. Are there any specific challenges students face with addition and subtraction in Class 5? |  |
| 5. How can addition and subtraction skills be applied in real-life situations? |  |
















