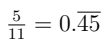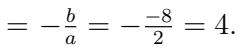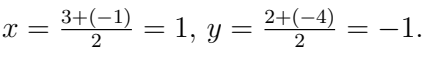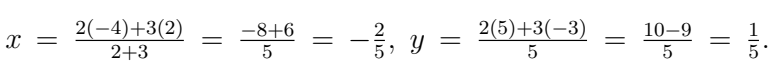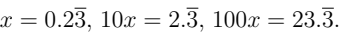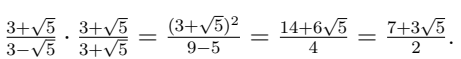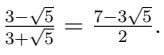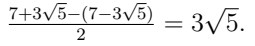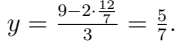Half Yearly Class 9 Mathematics Set 2 (Solutions) | Mathematics (Maths) Class 9 PDF Download
Time: 3 Hours
Maximum Marks: 80
General Instructions:
(i) The question paper comprises four sections: A, B, C, and D.
(ii) All questions are compulsory. However, internal choices are provided in some questions.
(iii) Section A has 10 Questions carrying 1 mark each.
(iv) Section B has 5 Questions carrying 2 marks each.
(v) Section C has 10 Questions carrying 3 marks each.
(vi) Section D has 5 Questions carrying 6 marks each.
(vii) Use of calculators is not permitted.
Section A
Q1. Is 2/7 a terminating decimal? (1 Mark)
Ans: No.
For 2/7, denominator 7 ≠ 2m · 5n. Non-terminating.
Q2. How many zeroes does the polynomial x2 − 4 have? (1 Mark)
Ans: 2
x2 − 4 = (x − 2)(x + 2), zeroes: x = 2, −2.
Q3. What is the x-coordinate of a point on the y-axis? (1 Mark)
Ans: 0
On y-axis, x-coordinate is 0.
Q4. If 2x − 3y = 6 is a linear equation, what is its slope? (1 Mark)
Ans: 2/3
Slope of 2x − 3y = 6: Rewrite y = 2/3 x - 2. Slope = 2/3
Q5. State Euclid’s third postulate. (1 Mark)
Ans: Euclid’s third postulate: A circle can be drawn with any center and radius.
Q6. If two angles of a triangle are complementary, what is the third angle? (1 Mark)
Ans: 90°
Complementary angles: x + y = 90°. Third angle: 180° − 90° = 90°.
Q7. Simplify: √12. (1 Mark)
Ans:
Q8. If p(2) = 0 for p(x) = x2 − kx + 4, find k. (1 Mark)
Ans: 4
p(2) = 22 − k · 2 + 4 = 0 ⇒ 4 − 2k + 4 = 0 ⇒ 2k = 8 ⇒ k = 4.
Q9. In which quadrant does (−4, −2) lie? (1 Mark)
Ans: (−4, −2): x < 0, y < 0, third quadrant.
Q10. If two lines are parallel, what is the measure of their corresponding angles? (1 Mark)
Ans: Equal.
Corresponding angles are equal.
Section B
Q1. Express 5/11 as a decimal. (2 Marks)
Ans:
Q2. Find the sum of the zeroes of 2x2 − 8x + 6. (2 Marks)
Ans: For 2x2 − 8x + 6, sum of zeroes
Q3. Find the coordinates of the point dividing A(3, 2) and B(−1, −4) in the ratio 1:1. (2 Marks)
Ans: (1, −1).
Ratio 1:1 is midpoint:
Q4. Solve 5x − 2y = 10 for x when y = 5. (2 Marks)
Ans: 5x − 2y = 10, y = 5: 5x − 2 · 5 = 10
⇒ 5x = 20
⇒ x = 4.
Q5. If ∠A = 40° and ∠B = 50° in ΔABC, Find ∠C. (2 Marks)
Ans: ∠C = 180° − (40° + 50°) = 90°.
Section C
Q1. Prove that √7 is irrational. (3 Marks)
Ans: Assume √7 = a/b, a, b coprime.
Then, 7 = a2/b2 ⇒ a2 = 7b2.
So, 7 divides a.
Let a = 7k.
Then, 49k2 = 7b2
⇒ b2 = 7k2, so 7 divides b. Contradiction.
Q2. Find the zeroes of x2 − 5x + 6. (3 Marks)
Ans: x2 − 5x + 6 = (x − 2)(x − 3) = 0.
Zeroes: x = 2, 3.
Q3. Find the coordinates of the point dividing A(2, −3) and B(−4, 5) in the ratio 2:3. (3 Marks)
Ans: Ratio 2 : 3:
Q4. Solve: 3x + 2y = 12 and x − y = 1 using elimination method. (3 Marks)
Ans: Multiply second by 2: 2x − 2y = 2.
Add to first: 3x + 2y + 2x − 2y = 12 + 2
⇒ 5x = 14
⇒ x = 14/5, y = 14/5 - 1 = 9/5.
Q5. Using Euclid’s axioms, explain why a point has no dimension. (3 Marks)
Ans: Things which are equal to the same thing are equal to one an- other. A point has no dimension as it has no length, width, or thickness.
Q6. If AB ∥ C D and a transversal intersects them, find the alternate interior angles if one angle is 70°. (3 Marks)
Ans: Alternate interior angles are equal. If one is 70°, the other is 70°.
Q7. Find k such that 3x2 + kx + 12 has equal roots. (3 Marks)
Ans: Discriminant: k2 − 4 · 3 · 12 = 0
⇒ k2 = 144
⇒ k = ±12.
Q8. Express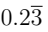 as a fraction. (3 Marks)
as a fraction. (3 Marks)
Ans:
Subtract: 90x = 21 ⇒ x = 21/90 = 7/30
Q9. Simplify: 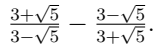 (3 Marks)
(3 Marks)
Ans:
Similarly,
Subtract:
Q10. Solve: 2x + 3y = 9 and 4x − y = 5 using elimination method. (3 Marks)
Ans: Multiply second by 3: 12x − 3y = 15.
Add to first: 2x + 3y + 12x − 3y = 9 + 15
⇒ 14x = 24
⇒ x = 12/7, y =
Section D
Q1. Find the quotient and remainder when x3 − 5x2 + 6x − 2 is divided by x − 2. (6 Marks)
Ans: Synthetic division: 1, −5, 6, −2 with x = 2: 1, 2 − 3, 0 + 6, 12 − 2
⇒ x2 − 3x + 6, remainder 10.
Q2. For points A(1, 1), B(5, 1), C (3, 4), find the distance AC and check if △ABC is equilateral. (6 Marks)
Ans:
Sides:√13,
AC = √13,
Not equilateral (only two sides equal).
Q3. Prove that alternate interior angles are equal for parallel lines cut by a transversal. (6 Marks)
Ans: Proved.
For AB ∥ CD, transversal PQ. ∠APQ = ∠CQP (same arcs).
Q4. Solve graphically: 2x + y = 8 and x − 2y = 1. Find the area of the triangle formed by these lines and the x-axis. (6 Marks)
Ans: For 2x + y = 8: (4, 0), (0, 8).
For x − 2y = 1: (3, 1), (1, 0).
Intersection x = 3, y = 2.
Triangle vertices: (3, 2), (4, 0), (1, 0).
Area: 1/2· 3 · 2 = 3 sq. units.
Q5.Solve: 3x − y = 7 and 2x + 3y = 1 using elimination method. Verify the solution. (6 Marks)
Ans: Multiply first by 3: 9x − 3y = 21.
Add to second: 9x − 3y + 2x + 3y = 21 + 1
⇒ 11x = 22
⇒ x = 2, y = −1.
Verify: 3 · 2 − (−1) = 7, 2 · 2 + 3(−1) = 1.
|
40 videos|560 docs|57 tests
|
FAQs on Half Yearly Class 9 Mathematics Set 2 (Solutions) - Mathematics (Maths) Class 9
| 1. What topics are typically covered in a Class 9 Half-Yearly Math exam? |  |
| 2. How can I prepare effectively for the Half-Yearly Math exam? |  |
| 3. What is the importance of solving previous years' question papers for the Half-Yearly Math exam? |  |
| 4. Are calculators allowed in the Class 9 Half-Yearly Math exam? |  |
| 5. What strategies can help reduce exam anxiety before the Half-Yearly Math exam? |  |