रेखीय और गैर-रेखीय प्रतिगमन | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year (Hindi) PDF Download
इस प्रकार, y का औसत x का एक रेखीय कार्य है, हालाँकि y का वैरिएंस x के मान पर निर्भर नहीं करता है। इसके अलावा, चूंकि त्रुटियाँ असंबंधित हैं, प्रतिक्रिया चर भी असंबंधित होते हैं। पैरामीटर β0 और β1 को आमतौर पर पुनरागमन गुणांक (regression coefficients) कहा जाता है। इन गुणांकों का एक सरल और अक्सर उपयोगी व्याख्या होती है। ढलान β1 वह परिवर्तन है जो x में एक इकाई परिवर्तन से y के वितरण के औसत में होता है। यदि x के डेटा की सीमा में x = 0 शामिल है, तो इंटरसेप्ट β0 वह औसत है जब x = 0 होता है। यदि x की सीमा में शून्य शामिल नहीं है, तो β0 का कोई व्यावहारिक अर्थ नहीं होता।
पैरामीटरों का कम से कम वर्ग अनुमान
कम से कम वर्ग की विधि का उपयोग β0 और β1 का अनुमान लगाने के लिए किया जाता है। अर्थात्, β0 और β1 का अनुमान इस प्रकार लगाया जाएगा कि अवलोकनों yi और सीधी रेखा के बीच के अंतर का वर्ग का योग न्यूनतम हो। समीकरण 1 को इस प्रकार लिखा जा सकता है:
yi = β0 + β1xi + εi, i = 1,2,...,n .......(4)
समीकरण 1 को जनसंख्या रिग्रेशन मॉडल के रूप में देखा जा सकता है, जबकि समीकरण 4 एक नमूना रिग्रेशन मॉडल है, जिसे n डेटा जोड़ों (yi, xi) (i = 1, 2, ..., n) के संदर्भ में लिखा गया है। इस प्रकार, कम से कम वर्ग मानदंड है:
- β0 और β1 के कम से कम वर्ग अनुमानक
इन दो समीकरणों को सरल बनाने से:
समीकरण 8 और 9 को कम से कम वर्ग सामान्य समीकरण कहा जाता है, और इन समकालिक समीकरणों का सामान्य समाधान है:
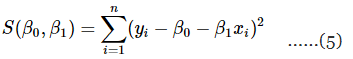
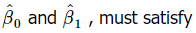
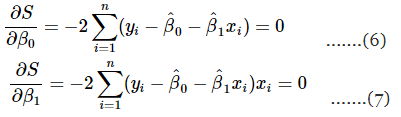
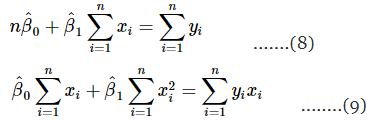
.......(10)
समीकरण 10 और 11 में, ये क्रमशः अवरोध और ढलान के कम से कम वर्ग अनुमानक हैं। इस प्रकार, फिट की गई सरल रेखीय रिग्रेशन मॉडल होगी:
...........(12)
समीकरण 12 एक विशेष x के लिए y के औसत का बिंदु अनुमान देता है। yi और xi के औसत दिए गए हैं:
...........(13)
और
...........(14)
समीकरण 11 का हरनिमेटर इस प्रकार लिखा जा सकता है:
और उस का हरनिमेटर इस प्रकार लिखा जा सकता है:
इसलिए, समीकरण 11 को एक सुविधाजनक तरीके से इस प्रकार लिखा जा सकता है:
.......(17)
अवलोकित मान yi और संबंधित फिट किए गए मान के बीच का अंतर एक अवशिष्ट है। गणितीय रूप से i का अवशिष्ट है:
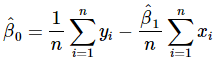

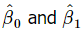
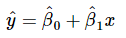
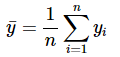
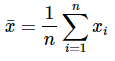
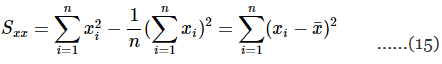
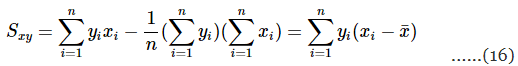
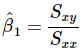
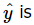
अवशिष्ट मॉडल की उपयुक्तता की जांच करने और अंतर्निहित धारणाओं से प्रस्थान की पहचान करने में महत्वपूर्ण भूमिका निभाते हैं।
गैर-रेखीय रिग्रेशन
गैर-रेखीय रिग्रेशन वैज्ञानिक डेटा का विश्लेषण करने के लिए एक शक्तिशाली उपकरण है, विशेष रूप से यदि आपको डेटा को रेखीय रिग्रेशन में फिट करने के लिए रूपांतरित करने की आवश्यकता हो। गैर-रेखीय रिग्रेशन का उद्देश्य उस डेटा के लिए एक मॉडल को फिट करना है जिसका आप विश्लेषण कर रहे हैं। आप उस मॉडल में परिवर्तनशीलों के सर्वोत्तम फिट मान खोजने के लिए एक कार्यक्रम का उपयोग करेंगे, जिसे आप वैज्ञानिक रूप से व्याख्या कर सकते हैं। हालांकि, एक मॉडल चुनना एक वैज्ञानिक निर्णय है और इसे केवल ग्राफ के आकार के आधार पर नहीं किया जाना चाहिए। जो समीकरण डेटा को सबसे अच्छा फिट करते हैं, वे वैज्ञानिक रूप से महत्वपूर्ण मॉडलों से मेल खाने की संभावना नहीं रखते हैं।
माइक्रोकंप्यूटरों के लोकप्रिय होने से पहले, अधिकांश वैज्ञानिकों के लिए गैर-रेखीय रिग्रेशन आसानी से उपलब्ध नहीं था। इसके बजाय, उन्होंने अपने डेटा को एक रेखीय ग्राफ बनाने के लिए रूपांतरित किया, और फिर रेखीय रिग्रेशन के साथ बदलित डेटा का विश्लेषण किया। इस प्रकार की विधि प्रयोगात्मक त्रुटि को विकृत कर देगी। रेखीय रिग्रेशन मानता है कि रेखा के चारों ओर बिंदुओं का बिखराव एक गॉसियन वितरण का पालन करता है, और मानक विचलन x के हर मान पर समान होता है। इसके अलावा, कुछ रूपांतरण स्पष्टीकरण वेरिएबल और प्रतिक्रिया वेरिएबल के बीच के संबंध को बदल सकते हैं। हालांकि सामान्यत: परिवर्तित डेटा का विश्लेषण करना उचित नहीं होता, लेकिन यह अक्सर डेटा को रेखीय रूपांतरण के बाद प्रदर्शित करने में सहायक होता है, क्योंकि मानव आंख और मस्तिष्क किनारों का पता लगाने के लिए विकसित हुए हैं, लेकिन आयताकार हाइपरबोलस या गुणात्मक क्षय वक्रों का पता लगाने के लिए नहीं।
गैर-रेखीय कम से कम वर्ग
स्वतंत्र और समान रूप से वितरित सामान्य त्रुटि की धारणा की वैधता या अनुमानित वैधता को देखते हुए, कोई केवल रेखीय नहीं बल्कि गैर-रेखीय रिग्रेशन मॉडलों में भी कम से कम वर्ग अनुमानक के बारे में कुछ सामान्य बयान कर सकता है। एक रेखीय रिग्रेशन मॉडल के लिए, पैरामीटरों के अनुमानक असत्य होते हैं, सामान्य रूप से वितरित होते हैं, और नियमित अनुमानकों के वर्ग में न्यूनतम संभावित वैरिएंस होता है। गैर-रेखीय रिग्रेशन मॉडल रेखीय रिग्रेशन मॉडलों से इस मायने में भिन्न होते हैं कि उनके पैरामीटरों के कम से कम वर्ग अनुमानक असत्य, सामान्य रूप से वितरित नहीं होते हैं, और न्यूनतम वैरिएंस के अनुमानक नहीं होते हैं। ये अनुमानक केवल असम्यतिक रूप से, अर्थात्, जैसे ही नमूना आकार अनंत के करीब पहुँचता है, इस गुण को प्राप्त करते हैं।
एक-परामीटर वक्र y = log(x−α) .......(19) इस मॉडल के अनुमान में सांख्यिकीय गुण अच्छे हैं, इसलिए यह अनुमान में अपेक्षाकृत सीधे रुख में व्यवहार करता है। एक और भी बेहतर व्यवहार वाला मॉडल प्राप्त किया जाता है जब α को एक अपेक्षित मान पैरामीटर से प्रतिस्थापित किया जाता है, जिससे y = log[x−x1 exp(y1)] ........(20) मिलता है, जहाँ y1 उस अपेक्षित मान का प्रतिनिधित्व करता है जो x = x1 के लिए है, जहाँ x1 को डेटा सेट में x मानों के देखे गए दायरे के भीतर कहीं चुना जाना चाहिए। ........(21) जब α<0 होता="" है,="" तो="">x=−1/α पर एक ऊर्ध्वाधर आसिंप्टोट होती है। y = exp(x−α) ......(22) वास्तव में, यह मॉडल एक छिपा हुआ अंतर्निहित रैखिक मॉडल है, क्योंकि इसे एक रैखिक मॉडल में पुनः पैरामीटरित किया जा सकता है। अर्थात्, α को एक अपेक्षित मान पैरामीटर y1 से प्रतिस्थापित करना, जो x = x1 के लिए है, y = y1exp(x−x1) .......(23) देता है, जो स्पष्ट रूप से y1 पैरामीटर में रैखिक है।
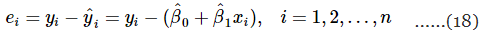
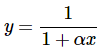
|
374 videos|1072 docs|1174 tests
|















