प्रतिगमन विश्लेषण - सहसंबंध और प्रतिगमन, व्यवसाय गणित और सांख्यिकी | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year (Hindi) PDF Download

परिचय पिछले अध्याय में हमने दो चर के बीच सांख्यिकीय संबंध की अवधारणा का अध्ययन किया, जैसे - उपयोग की गई उर्वरक की मात्रा और फसल की उपज; किसी उत्पाद की कीमत और उसकी आपूर्ति, बिक्री का स्तर और विज्ञापन की मात्रा आदि। ऐसे चर के बीच का संबंध उनके संघ के डिग्री और दिशा को संकेत करता है, लेकिन यह प्रश्न का उत्तर नहीं देता कि क्या दो चर के बीच कोई कार्यात्मक (या बीजगणितीय) संबंध है? यदि हां, तो क्या इसका उपयोग एक चर के सबसे संभावित मान का अनुमान लगाने के लिए किया जा सकता है, जब दूसरे चर का मान दिया जाए? "पुनरागमन विश्लेषण में हम एक अनुमान लगाने वाले समीकरण को विकसित करेंगे, अर्थात् एक गणितीय सूत्र जो ज्ञात चर को अज्ञात चर से संबंधित करता है। (फिर, जब हम इस संबंध के पैटर्न को सीख लेंगे, तो हम संघ विश्लेषण लागू कर सकते हैं ताकि यह निर्धारित किया जा सके कि चर कितनी अच्छी तरह से संबंधित हैं। संघ विश्लेषण, तब, हमें बताता है कि अनुमान लगाने वाला समीकरण वास्तव में संबंध का कितना अच्छा वर्णन करता है)। जिस चर का उपयोग अज्ञात चर का अनुमान लगाने के लिए किया जाता है उसे 'स्वतंत्र' या 'व्याख्यात्मक' चर कहा जाता है, और जिस चर का मान अनुमानित किया जाना है उसे 'निर्भर' या 'व्याख्यायित' चर कहा जाता है।" या-लुन चोउ संघ और पुनरागमन के बीच का अंतर संघ से हमारा तात्पर्य दो या अधिक चरों के बीच संबंध या संघ की डिग्री से है। संघ किसी कारण और प्रभाव के संबंध के बारे में कुछ भी अनुमान नहीं लगाता है। यहां तक कि संघ की उच्च डिग्री भी आवश्यक रूप से यह नहीं दर्शाती है कि दो चरों के बीच कारण और प्रभाव का संबंध है। जबकि पुनरागमन विश्लेषण के मामले में, Y और X के बीच एक कार्यात्मक संबंध होता है, जिससे Y के प्रत्येक मान के लिए केवल एक X का मान होता है। एक चर को निर्भर चर के रूप में पहचाना जाता है और अन्य को स्वतंत्र मूल्यवान के रूप में। यह अभिव्यक्ति स्वतंत्र मूल्यवानों के आधार पर निर्भर चर के मान का अनुमान लगाने के उद्देश्य से निकाली जाती है। पुनरागमन रेखाएँ पुनरागमन रेखा वह रेखा है जो एक चर के सबसे अच्छे औसत मानों को दूसरे के औसत मानों से मेल खाती है। दो श्रृंखलाओं X और Y के साथ, दो अंकगणितीय पुनरागमन रेखाएँ होती हैं, एक X के सर्वश्रेष्ठ औसत मानों को औसत Y के अनुसार दिखाती है और दूसरी Y के सर्वश्रेष्ठ औसत मानों को औसत X के अनुसार दिखाती है। बिखरे हुए आरेख के संदर्भ में, पुनरागमन रेखा वह सीधी रेखा है जो बिखरे हुए आरेख के लिए सबसे अच्छी तरह से फिट बैठती है। सबसे सामान्य रूप से उपयोग की जाने वाली मानदंड यह है कि यह सीधी रेखा निर्भर चर के अनुमानित और देखे गए मानों के बीच वर्गीकृत विचलनों के योग को न्यूनतम करती है। दो चरों X और Y के मामले में, X पर Y का पुनरागमन और Y पर X का पुनरागमन होने के कारण दो पुनरागमन रेखाएँ होंगी।

पुनरागमन समीकरण पुनरागमन समीकरण निकालने के विभिन्न तरीके हैं

• 1. X और Y के वास्तविक मानों को लेकर
• 2. वास्तविक औसत से विचलनों को लेकर
• 3. अनुमानित औसत से विचलनों को लेकर

Yc = a + bX जहां a और b को निम्नलिखित दो सामान्य समीकरणों को एक साथ हल करके पाया जा सकता है:

X पर Y का प्रतिगमन समीकरण निम्नलिखित रूप में व्यक्त किया गया है:

Xc = a + bY जहाँ a और b को निम्नलिखित दो सामान्य समीकरणों को समानांतर हल करके पाया जा सकता है:

उदाहरण 15: निम्नलिखित तालिका से पता करें: (1) Y पर X का प्रतिगमन समीकरण। (2) X पर Y का प्रतिगमन समीकरण।

समाधान: तालिका: प्रतिगमन समीकरणों की गणना

X पर Y का प्रतिगमन समीकरण इस प्रकार है: X = a + bY जहाँ a और b को निम्नलिखित 2 समीकरणों को समानांतर हल करके पाया जा सकता है –

तालिका से प्राप्त मानों को प्रतिस्थापित करते हुए, हमें मिलता है 96 = 6a + 120b ….(1) 2188 = 120a + 2754b ….(2) समीकरण 1 को 20 से गुणा करें और समीकरण 2 को इससे घटाएँ।

b = 0.76 इस b के मान को समीकरण ........ (1) में डालें 96 = 6a + 120 × 0.76 96 = 6a + 91.2 6a = 96 – 91.2

X पर Y के प्रतिगमन समीकरण में a और b के मान डालें

Y पर X का प्रतिगमन समीकरण इस प्रकार है Y = a + bX जहाँ स्थिरांक a और b को निम्नलिखित 2 सामान्य समीकरणों को समानांतर हल करके पाया जा सकता है—

ऊपर की तालिका से प्राप्त मानों को प्रतिस्थापित करते हुए, हमें मिलता है 120 = 6a + 96b ....(1) 2188 = 96a + 1758b ....(2) समीकरण 1 को 16 से गुणा करें और समीकरण 2 को इससे घटाएँ

समीकरण 1 में b का मान डालें 120 = 6a + 96 × 1.21 120 = 6a + 116.16 6a = 120 - 116.16 6a = 3.84

Y पर X के प्रतिगमन समीकरण में a और b के मान डालें Y = a + bX Y = 0.64 + 1.21X प्रतिगमन समीकरणों को खोजने का एक वैकल्पिक तरीका है। सामान्य समीकरणों के बजाय, संबंधित अंकगणितीय माध्य या अनुमानित माध्य से विचलन पर विचार किया जाता है: विधि II जब विचलन वास्तविक माध्य से लिए जाते हैं X और Y का प्रतिगमन समीकरण इस प्रकार है।

जहाँ X और Y श्रृंखलाओं का वास्तविक मीन क्रमशः है।

∑XY = X और Y के वास्तविक मीन से लिए गए अंतरों के उत्पाद का योग। ∑Y² = Y के वास्तविक मीन से लिए गए अंतरों का वर्ग का योग। Y और X का रिग्रेशन समीकरण इस प्रकार है।

∑XY = X और Y के वास्तविक मीन से लिए गए अंतरों के उत्पाद का योग। ∑X² = X के वास्तविक मीन से लिए गए अंतरों का वर्ग का योग।

उदाहरण 16: पिछले उदाहरण के डेटा से वास्तविक मीन से भिन्नताओं को लेकर दो रिग्रेशन समीकरण खोजें। समाधान: तालिका: रिग्रेशन समीकरणों की गणना।

X पर Y का रिग्रेशन समीकरण

bYX के मान को उपरोक्त समीकरण में डालते हैं एवं भी डालते हैं।

Y पर X का रिग्रेशन समीकरण

उपरोक्त समीकरण में bYX के मान को डालते हैं एवं भी डालते हैं।

विधि III जब भिन्नताएँ अनुमानित मीन से ली जाती हैं। यदि संबंधित श्रृंखलाओं का वास्तविक मीन पूर्णांक नहीं है बल्कि दशमलव में है, तो वास्तविक मीन से भिन्नताएँ निकालना कठिन हो जाता है क्योंकि सभी गणना किए गए मान भी दशमलव में होंगे। ऐसे में गणनाओं को सरल बनाने के लिए अनुमानित मीन से भिन्नताएँ ली जाती हैं। X पर Y का रिग्रेशन समीकरण इस प्रकार है।

Y पर X का रिग्रेशन समीकरण इस प्रकार है।

उदाहरण 17: निम्नलिखित तालिका से 2 रिग्रेशन समीकरण की गणना करें—

समाधान: तालिका: रिग्रेशन समीकरणों की गणना।

चूंकि ये पूर्णांक नहीं हैं, हम इसे X श्रृंखला से 15 और Y श्रृंखला से 25 का अनुमानित मीन लेकर हल करेंगे।

X पर Y का रिग्रेशन समीकरण

उपरोक्त तालिका से मान डालने पर हमें मिलता है।

Y और X का प्रतिगमन समीकरण

Y – 20.2 = 0.83 (X – 14.2)

• Y – 20.2 = 0.83X – 0.83 × 14.2
• Y = 0.83X – 11.78
• 20.2Y = 0.83X

सरल प्रतिगमन विश्लेषण

जबकि सहसंबंध विश्लेषण यह मानता है कि चर के बीच कोई कारणात्मक संबंध नहीं है, प्रतिगमन विश्लेषण यह मानता है कि एक चर एक पर निर्भर है:

• A) एक अन्य स्वतंत्र चर (सरल प्रतिगमन) पर, या
• B) कई स्वतंत्र चर (कई प्रतिगमन) पर।

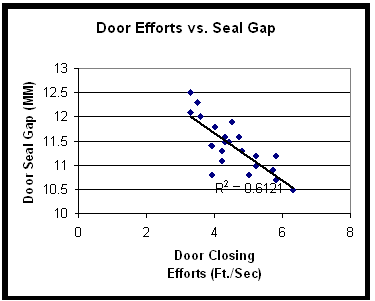
प्रतिगमन डेटा के लिए सर्वोत्तम फिट की रेखा को लीस्ट-स्क्वायर विधि का उपयोग करके तैयार करता है। आप नीचे एक उदाहरण देख सकते हैं जिसमें समान कार दरवाजे की बिखराव ग्राफ का उपयोग किया गया है:

आप देख सकते हैं कि डेटा रेखा के चारों ओर निकटता से क्लस्टरित है, और रेखा का ढाल नकारात्मक है। दो संबंधित सांख्यिकी द्वारा व्यक्त किया गया मजबूत नकारात्मक सहसंबंध है: r मान, जैसा कि पहले बताया गया है, -0.78 है और r² मान 0.61 है। R², जिसे निर्धारण गुणांक कहा जाता है, यह व्यक्त करता है कि निर्भर चर में परिवर्तनशीलता का कितना प्रतिशत स्वतंत्र चर में परिवर्तनशीलता द्वारा समझाया जाता है। आपको यह भी मिल सकता है कि एक गैर-रेखीय समीकरण जैसे कि एक घातांक या शक्ति कार्य एक बेहतर फिट प्रदान कर सकता है और एक रेखीय समीकरण की तुलना में उच्च r² प्राप्त कर सकता है। ये सांख्यिकीय गणनाएं Excel का उपयोग करके, या कई सांख्यिकीय विश्लेषण सॉफ़्टवेयर पैकेज का उपयोग करके की जा सकती हैं। MoreSteam सांख्यिकीय सॉफ़्टवेयर डाउनलोड के लिए लिंक प्रदान करता है, जिसमें मुफ्त सॉफ़्टवेयर भी शामिल है।

कई प्रतिगमन विश्लेषण

कई प्रतिगमन विश्लेषण सरल प्रतिगमन के समान पद्धति का उपयोग करता है, लेकिन इसमें एक से अधिक स्वतंत्र चर शामिल होते हैं। आर्थिक मॉडल एक अच्छा उदाहरण है, जहाँ GNP का निर्भर चर कई स्वतंत्र चर जैसे कि ब्याज दरें, उत्पादकता वृद्धि, सरकारी खर्च, बचत दरें, उपभोक्ता विश्वास आदि के संदर्भ में विश्लेषित किया जा सकता है। कई बार ऐतिहासिक डेटा का उपयोग कई प्रतिगमन में किया जाता है ताकि एक प्रक्रिया में सबसे महत्वपूर्ण इनपुट की पहचान की जा सके। इस प्रकार के विश्लेषण का लाभ यह है कि इसे बहुत तेजी से और अपेक्षाकृत सरलता से किया जा सकता है। हालाँकि, कई संभावित pitfalls हैं:

डेटा विभिन्न माप प्रणाली, कैलिब्रेशन ड्रिफ्ट, विभिन्न ऑपरेटरों, या रिकॉर्डिंग त्रुटियों के कारण असंगत हो सकता है।

• चर की सीमा बहुत सीमित हो सकती है, और यह कम सहसंबंध का झूठा संकेत दे सकती है। उदाहरण के लिए, किसी प्रक्रिया में तापमान नियंत्रण हो सकते हैं क्योंकि अतीत में पाया गया है कि तापमान का उत्पादन पर प्रभाव पड़ता है।
• इसलिए, ऐतिहासिक तापमान डेटा का उपयोग कम महत्व को दर्शा सकता है क्योंकि तापमान की सीमा पहले ही कड़ी सहिष्णुता में नियंत्रित है।
• एक समय अंतराल भी हो सकता है जो रिश्ते को प्रभावित करता है - उदाहरण के लिए, प्रक्रिया के प्रारंभिक चरण में तापमान महत्वपूर्ण हो सकता है, जबकि बाद में कम महत्वपूर्ण हो सकता है, या इसके विपरीत।
• यह भी संभव है कि इन्वेंटरी प्रभाव हों जिन्हें ध्यान में रखना आवश्यक है ताकि यह सुनिश्चित किया जा सके कि सभी माप एक ही प्रक्रिया के स्थिर बिंदु पर लिए जाएं।