क्वारटाइल विचलन - फैलाव के माप, व्यावसायिक गणित और सांख्यिकी | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year (Hindi) PDF Download
क्वारटाइल डेविएशन क्वारटाइल ऐसे मान होते हैं जो कुल अवलोकनों की संख्या को 4 समान भागों में विभाजित करते हैं। स्पष्ट रूप से, 3 क्वारटाइल होते हैं—
- (i) पहला क्वारटाइल (या निचला क्वारटाइल): Q1
- (ii) दूसरा क्वारटाइल (या मध्य क्वारटाइल): Q2
- (iii) तीसरा क्वारटाइल (या ऊपरी क्वारटाइल): Q3
Q1 से छोटे अवलोकनों की संख्या, Q1 और Q2 के बीच, या Q2 और Q3 के बीच, या Q3 से बड़े अवलोकनों की संख्या के समान होती है। निरंतर प्रकार के डेटा के लिए, एक चौथाई अवलोकन Q1 से छोटे होते हैं, दो चौथाई अवलोकन Q2 से छोटे होते हैं, और तीन चौथाई अवलोकन Q3 से छोटे होते हैं। इसका अर्थ है कि Q1, Q2, Q3 ऐसे मान हैं जो 'कम से कम' संचयी आवृत्तियों के लिए N/4, 2N/4, 3N/4 के अनुरूप होते हैं। चूंकि, 2N/4 = N/2 है, यह स्पष्ट है कि दूसरा क्वारटाइल Q2 माध्यिका के समान है।
Q1 < q2="" />< /> ; Q2 = माध्यिका। क्वारटाइल का उपयोग केंद्रीय प्रवृत्ति, फैलाव और झुकाव को मापने के लिए किया जाता है। उदाहरण के लिए, दूसरा क्वारटाइल Q2 स्वयं केंद्रीय प्रवृत्ति के माप के रूप में लिया जाता है, जहां इसे माध्यिका कहा जाता है। क्वारटाइल डेविएशन को ऊपरी और निचले क्वारटाइल के बीच के आधे अंतर के रूप में परिभाषित किया जाता है।
Q3 - Q1 का अंतर, जो क्वारटाइल के बीच की दूरी है, इसे इंटर क्वारटाइल रेंज भी कहा जा सकता है; इसका आधा सेमी-इंटर क्वारटाइल रेंज होता है। इस प्रकार 'सेमी-इंटर क्वारटाइल रेंज' नाम स्वयं क्वारटाइल डेविएशन की परिभाषा देता है।
क्वारटाइल डेविएशन (Q.D.) दो क्वारटाइल पर निर्भर है और सबसे बड़े 25% या सबसे छोटे 25% अवलोकनों की परिवर्तनशीलता पर विचार नहीं करता है। इसलिए यह चरम मानों से अप्रभावित रहता है। चूंकि अधिकांश मामलों में केंद्रीय 50% अवलोकन अपेक्षाकृत सामान्य होते हैं, Q.D. फैलाव का एक सुविधाजनक माप प्रदान करता है। इसे खुली श्रेणियों के साथ आवृत्ति वितरण से गणना किया जा सकता है। इस प्रकार Q.D. कई तरीकों से रेंज से बेहतर है। इसकी अप्रचलितता इसमें है कि Q.D. सभी अवलोकनों के आकारों पर निर्भर नहीं करता। Q.D. की गणना केवल दो क्वारटाइल, Q1 और Q3 की गणना पर निर्भर करती है, जिन्हें सरल अंतर्स्थान का उपयोग करके संचयी आवृत्ति वितरण से पाया जा सकता है।
उदाहरण और समाधान
उदाहरण 1: निम्नलिखित से क्वारटाइल डेविएशन की गणना करें:
समाधान: क्वारटाइल डेविएशन की गणना करने के लिए, हमें Q1 और Q3 खोजना है, अर्थात् संचयी आवृत्तियों के लिए मान N/4 और 3N/4 के अनुरूप मान। यहां, कुल आवृत्ति N = 82 है। इसलिए, N/4 = 20.5 और 3N/4 = 61.5।
उदाहरण 2. निम्नलिखित डेटा से उपयुक्त विसरण का माप निकालें: समाधान। चूंकि आवृत्ति वितरण में खुली श्रेणियाँ हैं, क्वारटाइल विचलन डेटा के लिए सबसे उपयुक्त विसरण का माप होगा। इसलिए, हमें क्वारटाइल Q1 और Q3 निर्धारित करने होंगे, जिसे सरल इंटरपोलेशन का उपयोग करके संचयी आवृत्ति वितरण से किया जा सकता है।
सरल इंटरपोलेशन लागू करते हुए,
उदाहरण 3. 10 CFA स्तर 1 उम्मीदवारों के निम्नलिखित स्कोर पर विचार करें: 78, 56, 67, 51, 43, 89, 57, 67, 78, 50 समाधान। रेंज = 89 - 43 = 46
उदाहरण 4. 6 निवेश विश्लेषकों ने छह अलग-अलग निवेशों पर निम्नलिखित रिटर्न प्राप्त किए: {12%, 4%, 23%, 8%, 9%, 16%} माध्य निरपेक्ष विचलन की गणना करें और इसका अर्थ बताएं। समाधान। पहले, हमें गणितीय माध्य की गणना करनी होगी: फिर, हम अब MAD की गणना कर सकते हैं: = 30/6 = 5% व्याख्या: इसका अर्थ है कि औसतन, एक व्यक्तिगत रिटर्न 12% के औसत रिटर्न से 5% विचलित होता है।
उदाहरण 5. ऊपर दिए गए उदाहरण 2 के डेटा के साथ काम करते हुए, वैरिएंस की गणना इस प्रकार की जाएगी: समाधान। इस प्रकार, औसत परिवर्तन (0.12) से 0.003767 है। मानक विचलन 0.0037671/2 = 0.06137 या 6.14% है। विश्लेषक रिटर्न की व्याख्या के लिए मानक विचलन का उपयोग करते हैं, जबकि वैरिएंस की तुलना में इसे समझना बहुत आसान होता है।
उदाहरण 6. मान लीजिए कि ऊपर दिए गए उदाहरण 2 में प्राप्त रिटर्न 100 रिटर्न के जनसंख्या से लिए गए थे। नमूना माध्य और संबंधित नमूना वैरिएंस की गणना करें। समाधान। नमूना माध्य अब भी 12% होगा। इसलिए,

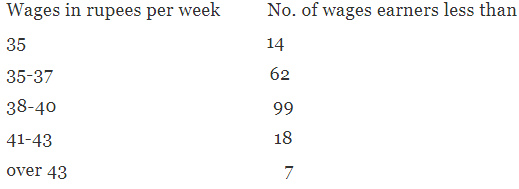
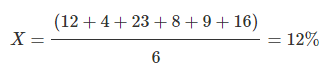
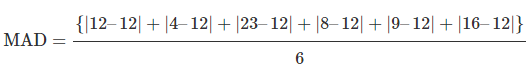
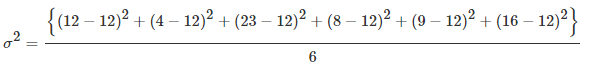
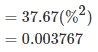
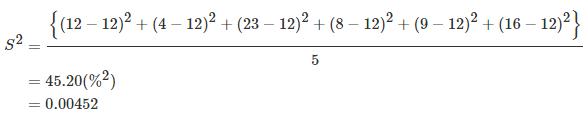
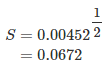
|
374 videos|1072 docs|1174 tests
|















