सारांश: मात्रात्मक तर्कशक्ति | General Intelligence & Reasoning for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

परिमाणात्मक तर्क क्या है?

• परिमाणात्मक तर्क वह क्षमता है जो गणितीय समस्याओं को समझने और हल करने की होती है, जिसमें बुनियादी अंकगणितीय क्रियाएँ जैसे जोड़, घटाव, गुणा और भाग शामिल हैं।
• परिमाणात्मक तर्क प्रश्न सभी प्रकार की योग्यता परीक्षाओं में सामान्य होते हैं और छात्र को समस्या में परिभाषित मानकों के अनुसार संख्यात्मक संबंधों को हल करने की आवश्यकता होती है।
• परिमाणात्मक तर्क केवल गणना करने की क्षमता के बारे में नहीं है, बल्कि अंतर्निहित अवधारणाओं को समझने, पैटर्न को पहचानने और संख्यात्मक डेटा के आधार पर सूचित निर्णय लेने की भी आवश्यकता है।
• अंकगणितीय तर्क उम्मीदवार के गणितीय ज्ञान का परीक्षण करता है। अंकगणितीय तर्क पर आधारित प्रश्न आमतौर पर संख्यात्मक होते हैं, इसलिए इनमें कई मामलों में गणना भाग शामिल होते हैं।
• जो उम्मीदवार गणित पसंद नहीं करते, वे अंकगणितीय तर्क अनुभाग को अपने लिए अनुकूल नहीं पाएंगे, लेकिन स्पष्ट अवधारणाओं और अभ्यास के साथ वे इस अनुभाग में आसानी से अच्छे अंक प्राप्त कर सकते हैं।

उदाहरण: क्लासिक परिमाणात्मक तर्क प्रश्न:

• एक व्यक्ति एक नई स्वास्थ्य बीमा लेना चाहता है। इससे संबंधित मामलों का ध्यान रखने वाला एक अधिकारी उस व्यक्ति से कहता है, "कृपया बताएं कि आपके कितने बच्चे हैं।" व्यक्ति उत्तर देता है, "मेरे तीन बच्चे हैं।" अधिकारी पूछता है, "आपके बच्चों की उम्र क्या है?" व्यक्ति उत्तर देता है, "उम्र का गुणनफल 36 के बराबर है।" अधिकारी उत्तर देता है, "यह पर्याप्त जानकारी नहीं है, सर!" व्यक्ति जवाब देता है, "मुझे खेद है कि मैं थोड़ा अस्पष्ट था, लेकिन उम्र का योग आपके ऑफिस के सामने की दुकानों की संख्या के बराबर है।" अधिकारी: "यह अभी भी पर्याप्त जानकारी नहीं है, सर!" व्यक्ति उत्तर देता है, "मेरे सबसे बड़े बच्चे को चॉकलेट पसंद है।" अधिकारी: "आपके सहयोग के लिए धन्यवाद, अब मुझे उम्र पता है।" क्या आप अधिकारी के समान बुद्धिमान हैं? तो, बच्चों की उम्र का योग बताएं। विकल्प: 1. 13 2. 22 3. 36 4. 38
• हल: उम्र का गुणनफल 36 है। इसका उपयोग करके, आप उम्र के निम्नलिखित संयोजन बना सकते हैं:
• 1, 36; योग = 37
• 1, 18, 2; योग = 21
• 1, 12, 3; योग = 16
• 1, 9, 4; योग = 14
• 1, 6, 6; योग = 13
• 2, 9, 2; योग = 13
• 2, 6, 3; योग = 11
• 3, 3, 4; योग = 10
• जब व्यक्ति ने कहा कि उम्र का गुणनफल 36 है, तब अधिकारी को पर्याप्त जानकारी नहीं मिली। फिर जब उसे बताया गया कि योग आपके ऑफिस के सामने की दुकानों की संख्या के बराबर है, तो उसने यह कहकर जवाब दिया कि यह अभी भी पर्याप्त जानकारी नहीं है। इसलिए, उम्र का योग 13 होना चाहिए, क्योंकि अन्यथा वह तुरंत उम्र जान जाता। अंतिम बयान यह है कि सबसे बड़े बच्चे को चॉकलेट पसंद है। इसलिए, एक सबसे बड़ा बच्चा है। इस प्रकार अधिकारी निष्कर्ष निकालता है कि बच्चों की उम्र 2, 2 और 9 वर्ष है। इसलिए, विकल्प (1) सही उत्तर है।

परिमाणात्मक तर्क प्रश्नों को हल करने के लिए आवश्यक कौशल

मात्रात्मक तर्क प्रश्नों को हल करने के लिए आवश्यक कौशल

मात्रात्मक तर्क प्रश्नों को सफलतापूर्वक हल करने के लिए कई महत्वपूर्ण कौशल आवश्यक हैं:

• विशिष्ट तर्क को समझना: प्रश्नों में प्रस्तुत विशेष संख्यात्मक तर्क को समझने की क्षमता।
• संकेतों को सही क्रम में व्यवस्थित करना: दिए गए संकेतों को सही अनुक्रम में व्यवस्थित करना, तार्किक तर्क के सिद्धांतों का पालन करते हुए।
• बुनियादी गणितीय अवधारणाओं को समझना: प्रतिशत, औसत, अनुपात, और गुणा जैसी बुनियादी गणितीय अवधारणाओं से परिचित होना।
• प्रतीकात्मक प्रतिनिधित्व बनाना: संकेतों को प्रतीकात्मक रूप में प्रस्तुत करने की क्षमता, जिससे संबंधित जानकारी को संयोजित और विश्लेषण करना आसान हो जाता है।
• समय और धैर्य: प्रश्न में दिए गए अप्रत्यक्ष संकेतों का उपयोग कब करना है, यह जानना और समस्या समाधान के दौरान उपयुक्त क्षण की प्रतीक्षा करना।

उदाहरण

Q1: 5, 11, 24.2, 53.24, ?, 257.6816

समाधान: 5 x 2.2 = 11
11 x 2.2 = 24.2
24.2 x 2.2 = 53.24
53.24 x 2.2 = 117.128
117.128 x 2.2 = 257.6816
इस प्रकार, सही उत्तर 117.128 है।

Q2: 71 : 42 :: 98 : ?

समाधान: 71 – 29 = 42
इसी प्रकार, 98 – 29 = 69
इस प्रकार, 69 प्रश्न चिह्न को प्रतिस्थापित करेगा।

Q3: 71 : 42 :: 98 : ?

समाधान: 71 – 29 = 42
इसी प्रकार, 98 – 29 = 69
इस प्रकार, 69 प्रश्न चिह्न को प्रतिस्थापित करेगा।

Q4: 67 : 76 :: 42: ?

समाधान: 67 + 9 = 76
इसी प्रकार, 42 + 9 = 51
इस प्रकार, 51 प्रश्न चिह्न को प्रतिस्थापित करेगा।

Q5: 49, 121, 169, ?, 361

समाधान: श्रृंखला का समाधान निम्नलिखित है।
7² = 49
11² = 121
13² = 169
17² = 289
19² = 361
इस प्रकार, सही उत्तर 289 है।

Q6: संख्या 381576 में कितने अंकों की स्थिति उस समय समान रहेगी जब संख्या को आरोही क्रम में व्यवस्थित किया जाएगा?

समाधान: मूल संख्या रूप है: 3 8 1 5 7 6
आरोही क्रम रूप है: 1 3 5 6 7 8
यदि हम उन संख्याओं की स्थिति की जांच करें जिनकी स्थिति दोनों रूपों में समान रहेगी, तो हम देखेंगे कि केवल संख्या 7 की स्थिति समान या अपरिवर्तित रहती है।
इस प्रकार, सही उत्तर 1 है।

Q7: यदि 3x - 7 = 20, तो x का मान क्या है?

समाधान: 3x - 7 = 20
3x = 20 + 7
3x = 27
x = 27 / 3
x = 9

Q8: एक कार 6 घंटे में 360 मील चलती है। इसकी औसत गति क्या है?

समाधान: औसत गति = कुल दूरी / कुल समय
औसत गति = 360 मील / 6 घंटे
औसत गति = 60 मील प्रति घंटे

Q9: 120 का 35% क्या है?

समाधान: 35% of 120 = (35/100) * 120 = 42

Q10: यदि एक आयत का क्षेत्रफल 180 वर्ग इकाइयाँ है और इसकी लंबाई 12 इकाइयाँ है, तो इसकी चौड़ाई क्या होगी?

समाधान: आयत का क्षेत्रफल = लंबाई * चौड़ाई
180 = 12 * चौड़ाई
चौड़ाई = 180 / 12
चौड़ाई = 15 इकाइयाँ

Q11: y के लिए हल करें: 4y + 5 = 3y + 12

समाधान: 4y + 5 = 3y + 12
4y - 3y = 12 - 5
y = 7

Q12: 40 छात्रों की कक्षा में, 12 छात्र लड़कियाँ हैं। कक्षा में लड़कियों का प्रतिशत क्या है?

समाधान: लड़कियों का प्रतिशत = (लड़कियों की संख्या / कुल छात्रों) * 100
लड़कियों का प्रतिशत = (12 / 40) * 100
लड़कियों का प्रतिशत = 30%

Q13: एक स्टोर एक जैकेट पर 25% छूट दे रहा है, जिसकी मूल कीमत $80 है। जैकेट की बिक्री मूल्य क्या होगी?

समाधान: छूट राशि = 25% of $80 = (25/100) * $80 = $20
बिक्री मूल्य = मूल कीमत - छूट राशि
बिक्री मूल्य = $80 - $20 = $60

Q14: यदि एक ट्रेन 75 मील प्रति घंटे की गति से 2 घंटे और 45 मिनट चलती है, तो वह कितनी दूर चलती है?

समाधान: समय को घंटों में: 2 घंटे (45 मिनट / 60 मिनट) = 2.75 घंटे
दूरी = गति * समय
दूरी = 75 मील/घंटा * 2.75 घंटे = 206.25 मील

Q15: पहले दस सकारात्मक विषम संख्याओं का योग क्या है?

समाधान: पहले दस सकारात्मक विषम संख्याएँ हैं: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
योग = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 100

Q16: एक आयताकार बगीचे का परिधि 60 मीटर है, और इसकी चौड़ाई 10 मीटर है। इसकी लंबाई क्या होगी?

समाधान: आयत का परिधि = 2 * (लंबाई + चौड़ाई)
60 = 2 * (लंबाई + 10)
30 = लंबाई + 10
लंबाई = 20 मीटर

Q17: यदि तीन लगातार सम संख्याओं का योग 78 है, तो सबसे बड़ी संख्या क्या है?

समाधान: संख्याएँ x, x + 2, और x + 4 हैं।
x + (x + 2) + (x + 4) = 78
3x + 6 = 78
3x = 72
x = 24
सबसे बड़ी संख्या है x + 4 = 24 + 4 = 28

Q18: एक फल विक्रेता ने 120 किलोग्राम सेब को $4 प्रति किलोग्राम और 80 किलोग्राम संतरे को $5 प्रति किलोग्राम बेचा। उसने कुल कितना पैसा कमाया?

समाधान: सेब से पैसा = 120 किलोग्राम * $4 = $480
संतरे से पैसा = 80 किलोग्राम * $5 = $400
कुल कमाई = $480 + $400 = $880

Q19: सबसे छोटा सकारात्मक पूर्णांक जो 6 और 8 दोनों से विभाज्य है, क्या है?

समाधान: 6 और 8 का न्यूनतम समापवर्त्य (LCM) ज्ञात करें।
6 के मुख्य गुणांक = 2 * 3
8 के मुख्य गुणांक = 2³
LCM = 2³ * 3 = 24
सबसे छोटा सकारात्मक पूर्णांक 24 है।

Q20: निम्नलिखित समीकरण को हल करें: 5(x - 3) = 4(x + 2)

समाधान: 5(x - 3) = 4(x + 2)
5x - 15 = 4x + 8
5x - 4x = 15 + 8
x = 23

Q21: एक कार रेंटल कंपनी $20 प्रति दिन और प्रति मील $0.15 का अतिरिक्त शुल्क लेती है। 3 दिनों के लिए कार किराए पर लेने और 200 मील चलाने की लागत कितनी होगी?

समाधान: 3 दिनों की लागत = 3 * $20 = $60
200 मील की लागत = 200 * $0.15 = $30
कुल लागत = $60 + $30 = $90

Q22: यदि 9 किताबों का वजन 36 पाउंड है, तो 15 किताबों का वजन कितना होगा?

समाधान: 1 किताब का वजन = 36 पाउंड / 9 किताबें = 4 पाउंड/किताब
15 किताबों का वजन = 15 किताबें * 4 पाउंड/किताब = 60 पाउंड

Q23: संख्याओं 18, 24, और 30 का औसत क्या है?

समाधान: औसत = (संख्याओं का योग) / (संख्याओं की संख्या)
औसत = (18 + 24 + 30) / 3
औसत = 72 / 3 = 24

Q24: यदि एक वर्ग की भुजा की लंबाई 8 इकाइयाँ है, तो उसकी विकर्ण की लंबाई क्या होगी?

समाधान: विकर्ण की लंबाई = भुजा की लंबाई * √2
विकर्ण की लंबाई = 8 * √2 = 8√2 इकाइयाँ

Q25: एक स्टोर प्रति पैक $4.50 में 6 पेन के पैक बेचता है। 3 पैकों की लागत कितनी होगी?

समाधान: 3 पैकों की लागत = 3 * $4.50 = $13.50

Q26: एक व्यक्ति $1000 को 4% वार्षिक ब्याज दर के साथ एक बचत खाते में निवेश करता है। 2 वर्षों के बाद खाते में बैलेंस क्या होगा?

समाधान: A = P(1 + r/n)^(nt)
जहाँ A अंतिम राशि है, P मूलधन है, r ब्याज दर है, n एक वर्ष में ब्याज के कितनी बार जोड़ने की दर है, और t वर्षों की संख्या है।
A = 1000(1 + 0.04/1)^(1*2)
A = 1000(1 + 0.04)²
A = 1000(1.04)²
A = 1000 * 1.0816
A = 1081.60
2 वर्षों के बाद खाते में बैलेंस $1081.60 है।

अंकगणित तर्क सूत्र

अंकगणित तर्क में समस्याओं को हल करने के लिए अक्सर मूलभूत सूत्रों का उपयोग किया जाता है। यहां कुछ सामान्य अंकगणितीय सूत्रों की सूची दी गई है, जो सहायक हो सकते हैं:

• जोड़: a + b = c
• घटाव: a - b = c
• गुणन: a * b = c
• भाग: a / b = c
• औसत: (a + b + c + ... + n) / n
• प्रतिशत: (भाग/कुल) * 100
• अनुपात: a : b
• अनुपात समानता: a / b = c / d
• दूरी: गति * समय
• गति: दूरी / समय
• समय: दूरी / गति
• सरल ब्याज: I = P * R * T / 100 (जहां I = ब्याज, P = प्रधान, R = दर, और T = समय)
• संवृद्धि ब्याज: A = P(1 + r/n)^(nt) (जहां A = राशि, P = प्रधान, r = वार्षिक ब्याज दर, n = प्रति वर्ष ब्याज की संख्या, और t = वर्षों में समय)
• लाभ या हानि: लाभ = बिक्री मूल्य - लागत मूल्य (हानि = लागत मूल्य - बिक्री मूल्य)
• प्रतिशत वृद्धि या कमी: (नया मूल्य - पुराना मूल्य) / पुराना मूल्य * 100
• भिन्न:
  • जोड़: a/b + c/d = (ad + bc) / bd
  • घटाव: a/b - c/d = (ad - bc) / bd
  • गुणन: (a/b) * (c/d) = (a * c) / (b * d)
  • भाग: (a/b) ÷ (c/d) = (a * d) / (b * c)
• दशमलव से भिन्न: दशमलव को भिन्न में बदलने के लिए, दशमलव को अंश के रूप में लिखें और हर दशमलव स्थान के आधार पर हर सौ का घातांक को हर अंश के रूप में रखें। फिर, भिन्न को सरल बनाएं।
• भिन्न से दशमलव: अंश को हर हर के द्वारा भाग करें।
• भिन्न से प्रतिशत: (भिन्न) * 100
• प्रतिशत से भिन्न: (प्रतिशत) / 100
• प्रतिशत से दशमलव: (प्रतिशत) / 100
• दशमलव से प्रतिशत: (दशमलव) * 100
• भारित औसत: (w1 * x1 + w2 * x2 + ... + wn * xn) / (w1 + w2 + ... + wn)

भारित औसत: (w1 * x1 + w2 * x2 + ... + wn * xn) / (w1 + w2 + ... + wn)

• न्यूनतम समापवर्तक (LCM): सबसे छोटा गुणांक जो प्रत्येक संख्या द्वारा ठीक से विभाजित होता है।
• महत्तम समापवर्तक (GCD): सबसे बड़ा संख्या जो दो या अधिक संख्याओं को बिना शेष के विभाजित करता है।
• प्राइम संख्या: एक संख्या जो 1 से बड़ी होती है और जिसके केवल दो गुणांक होते हैं: 1 और स्वयं।
• गुणांक: वे संख्याएँ जिन्हें मिलाकर मूल संख्या प्राप्त की जा सकती है।
• संख्याएँ का वर्ग: a² = a * a
• संख्याएँ का घन: a³ = a * a * a
• वर्गमूल: √a वह संख्या है, जिसे स्वयं से गुणा करने पर a प्राप्त होता है।
• घनमूल: ∛a वह संख्या है, जिसे स्वयं से तीन बार गुणा करने पर a प्राप्त होता है।
• व्यवस्थाएँ (Permutations): nPr = n! / (n - r)!, जहाँ n कुल तत्वों की संख्या है और r चुने गए तत्वों की संख्या है।
• संयोग (Combinations): nCr = n! / [r!(n - r)!], जहाँ n कुल तत्वों की संख्या है और r चुने गए तत्वों की संख्या है।

ये अंकगणितीय सूत्र मूलभूत अवधारणाएँ कवर करते हैं और विभिन्न समस्या-समाधान स्थितियों में लागू किए जा सकते हैं। हालाँकि, ध्यान रखें कि अधिक उन्नत अंकगणितीय समस्याओं के लिए अतिरिक्त सूत्रों या इन मूल सूत्रों के संयोजन की आवश्यकता हो सकती है।

अंकगणितीय तर्क के प्रकार

गणितीय तर्क के प्रकार

आइए देखते हैं उन विभिन्न प्रकार के गणितीय तर्क प्रश्नों को जो आपके आगामी प्रतिस्पर्धी परीक्षाओं में आ सकते हैं।

1. पहेली

इस प्रकार के गणितीय तर्क प्रश्नों में, उम्मीदवारों को दी गई जानकारी का विश्लेषण करना होता है, महत्वपूर्ण जानकारी को चुनना होता है, और उन जानकारियों को छोड़ना होता है जो दिए गए प्रश्नों के सेट को हल करने में आवश्यक नहीं होती।

2. उपमा

इस प्रकार के गणितीय तर्क प्रश्नों में, उम्मीदवारों को प्रश्न में दिए गए शब्दों के समान एक शब्द या शब्दों का जोड़ा ढूंढना होता है।

3. श्रृंखला

इस प्रकार के गणितीय तर्क प्रश्नों में, उम्मीदवारों को प्रदान की गई श्रृंखला में से गायब या गलत संख्या को खोजने की आवश्यकता होती है। कुछ प्रश्नों में, दी गई श्रृंखला में से एक शब्द गलत हो सकता है, और उम्मीदवारों को श्रृंखला के निर्माण में शामिल पैटर्न की पहचान करके उस शब्द को खोजना होगा।

4. विषमलंबता

इस प्रकार के गणितीय तर्क प्रश्नों में, उम्मीदवारों को विभिन्न संकेतों के बारे में जानना आवश्यक है, जो इस प्रकार के प्रश्नों में उपयोग किए जाते हैं। नीचे दिए गए हैं:

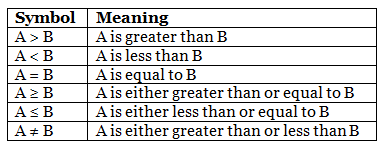
5. वैन आरेख

वैन आरेख एक प्रतिनिधित्व विधि है, जो एकल चित्र में एक निर्दिष्ट समूह के तत्वों के बीच सभी संभावित संबंधों को दर्शाती है। वैन आरेख सेटों के बीच संबंध व्यक्त करने का सबसे आसान तरीका है।

6. घन और पासा

इस प्रकार के गणितीय तर्क प्रश्नों में, एकल या कई घन और पासे पर आधारित समस्याएँ पूछी जाती हैं और उम्मीदवारों को दी गई छवि का विश्लेषण करके सही उत्तर देना होता है।

गणितीय तर्कशक्ति के टिप्स और तरकीबें

गणितीय तर्कशक्ति के प्रश्नों को हल करने के लिए एक चरण-दर-चरण दृष्टिकोण अपनाना आसान हो सकता है। यहाँ कुछ गणितीय तर्कशक्ति के टिप्स और तरकीबें दी गई हैं जो आपको इन समस्याओं को अधिक प्रभावी ढंग से निपटने में मदद करेंगी:

• प्रश्न को ध्यान से पढ़ें: यह सुनिश्चित करें कि आप गणितीय तर्कशक्ति प्रश्न के समस्या कथन को पूरी तरह से समझते हैं और दिए गए जानकारी की पहचान करें, साथ ही यह भी जानें कि आपको क्या पता करना है।
• समस्या को विभाजित करें: जटिल गणितीय समस्याओं को छोटे, अधिक प्रबंधनीय हिस्सों में विभाजित कर सरल बनाएं। दिए गए डेटा के बीच अंतर्निहित अवधारणाओं और संबंधों की पहचान करें।
• सही सूत्र या विधि चुनें: पहचानी गई जानकारी और संबंधों के आधार पर, समस्या को हल करने के लिए उपयुक्त गणितीय सूत्र या विधि का चयन करें।
• डेटा को व्यवस्थित करें: दिए गए डेटा और किसी भी अतिरिक्त जानकारी को व्यवस्थित रूप से रखें। यह तालिका, आरेख, या समीकरण के रूप में हो सकता है।
• गणनाएँ करें: चयनित गणितीय सूत्र या विधि को लागू करें और आवश्यक गणनाएँ करें। यदि लागू हो, तो इकाइयों का ध्यान रखें और अपनी गणनाओं की सटीकता सुनिश्चित करें।
• अपने काम की जांच करें: अपनी गणनाओं की सटीकता की पुष्टि करें और सुनिश्चित करें कि आपका उत्तर समस्या के संदर्भ में तार्किक रूप से सही है। यदि आवश्यक हो, तो अपने चरणों को फिर से देखें और किसी भी त्रुटियों की पहचान करें।
• उत्तर को सरल बनाएं: यदि आवश्यक हो, तो अपने उत्तर को सबसे उपयुक्त प्रारूप में व्यक्त करके सरल बनाएं, जैसे कि भिन्न, दशमलव, या प्रतिशत।
• प्रश्न की समीक्षा करें: समस्या कथन पर वापस जाएं और सुनिश्चित करें कि आपका उत्तर पूछे गए प्रश्न का समाधान करता है। यदि प्रश्न में कई भाग हैं, तो यह सुनिश्चित करें कि आपने सभी पहलुओं को संबोधित किया है।

• सही सूत्र या विधि चुनें: पहचाने गए जानकारी और संबंधों के आधार पर, समस्या को हल करने के लिए उपयुक्त अंकगणितीय सूत्र या विधि का चयन करें।

सही सूत्र या विधि चुनें: पहचाने गए जानकारी और संबंधों के आधार पर, समस्या को हल करने के लिए उपयुक्त अंकगणितीय सूत्र या विधि का चयन करें।

• अपने कार्य की जांच करें: अपने गणनाओं की सटीकता की पुष्टि करें और सुनिश्चित करें कि आपका उत्तर समस्या के संदर्भ में तार्किक रूप से सही है। यदि आवश्यक हो, तो अपने कदमों को फिर से देखें और किसी भी त्रुटियों की पहचान करें।

अपने कार्य की जांच करें: अपने गणनाओं की सटीकता की पुष्टि करें और सुनिश्चित करें कि आपका उत्तर समस्या के संदर्भ में तार्किक रूप से सही है। यदि आवश्यक हो, तो अपने कदमों को फिर से देखें और किसी भी त्रुटियों की पहचान करें।

• प्रश्न की समीक्षा करें: समस्या के विवरण पर वापस जाएं और सुनिश्चित करें कि आपका उत्तर जो पूछा गया है, उसे संबोधित करता है। यदि प्रश्न में कई भाग हैं, तो सुनिश्चित करें कि आपने सभी पहलुओं को संबोधित किया है।

प्रश्न की समीक्षा करें: समस्या के विवरण पर वापस जाएं और सुनिश्चित करें कि आपका उत्तर जो पूछा गया है, उसे संबोधित करता है। यदि प्रश्न में कई भाग हैं, तो सुनिश्चित करें कि आपने सभी पहलुओं को संबोधित किया है।