Chapter Notes: Exponents and Powers

Table of Contents
1. Introduction
2. Power with Negative Exponents
3. Law of Exponents
4. Use of Exponents to Express Small Numbers in Standard Form
5. Comparing Very Large and Very Small Numbers
6. Points to Remember
View more

Introduction

Exponents and powers are fundamental concepts in mathematics that simplify the expression of large numbers and complex calculations. An exponent indicates how many times a number, called the base, is multiplied by itself.

• Example: In the expression 2³ (read as "2 raised to the power of 3").
• Here, 2 is the base, and 3 is the exponent.
• This expression means that 2 is multiplied by itself three times:
• i.e, 2  × 2 × 2 = 8

Another Example,

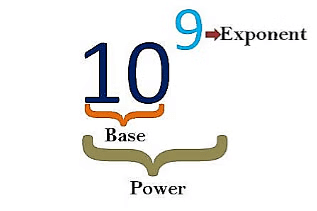
• Here 10 is the base and 9 is the exponent and this complete number is the power.
• The exponent could be positive or negative. 
• This tells us that the number 10 will be multiplied 9 times,
• like, 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10

Power with Negative Exponents

 100^-3 =  1100³

This shows that for any non-zero negative integers a:

a^-m =  1a^m where m is the positive integer and a^m is the multiplicative inverse of a^-m.

Example:  Simplify the following 

(1) 6^-2 

(2) 4^-5

(3) y^-7

Ans:  

1. 6^-2 =  16² = 136

2.  4^-5 =  14⁵ = 11024

3. y^-7 =  1y⁷

Law of Exponents

If we have a and b as the base and m and n as the exponents, then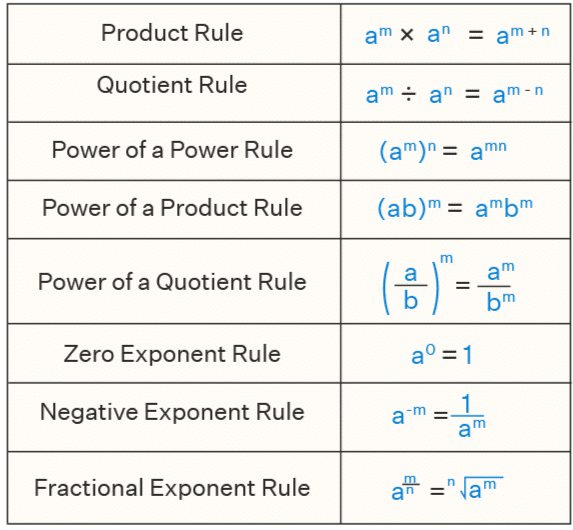 

Some Examples

Problem: Simplify the expression $3\mathrm{<sup\; style="font-size:12px\; !important">4</sup>}\times 3\mathrm{<sup\; style="font-size:12px\; !important">2</sup>}$.

Solution:

1. Identify the Base: In this expression, the base is $33$.

2. Apply the Rule of Exponents: When multiplying two expressions with the same base, we add the exponents. The rule is:

   $a\mathrm{<sup\; style="font-size:12px\; !important">m</sup>}\times a\mathrm{<sup\; style="font-size:12px\; !important">n</sup>}=a\mathrm{<sup\; style="font-size:12px\; !important">m</sup>}$⁺ⁿ

   Here, $m=4m\; =\; 4$ and $n=2n\; =\; 2$

3. Add the Exponents:

   $3\mathrm{<sup\; style="font-size:12px\; !important">4</sup>}\times 3\mathrm{<sup\; style="font-size:12px\; !important">2</sup>}=3\mathrm{<sup\; style="font-size:12px\; !important">4+2</sup>}$⁺²=3⁶

4. Calculate $3^6$3⁶:

   $3\mathrm{<sup\; style="font-size:12px\; !important">6</sup>}=3\times 3\times 3\times 3\times 3\times 33^6\; =\; 3\; \backslash times\; 3\; \backslash times\; 3\; \backslash times\; 3\; \backslash times\; 3\; \backslash times\; 3$
   • Calculating step by step:
     • $3\times 3=93\; \backslash times\; 3\; =\; 9$
     • $9\times 3=279\; \backslash times\; 3\; =\; 27$
     • $27\times 3=8127\; \backslash times\; 3\; =\; 81$
     • $81\times 3=\mathrm{243\; and\; so\; on }81\; \backslash times\; 3\; =\; 243$

So, 3⁶ =729$3^6\; =\; 729$

Final Answer:

$3\mathrm{<sup\; style="font-size:12px\; !important">4</sup>}\times 3\mathrm{<sup\; style="font-size:12px\; !important">2</sup>}=3\mathrm{<sup\; style="font-size:12px\; !important">6</sup>}=7293^4\; \backslash times\; 3^2\; =\; 3^6\; =\; 729$

Use of Exponents to Express Small Numbers in Standard Form

Sometimes, we need to write the numbers in very small or large form, and we can use the exponents to represent the numbers in small numbers.

1. Standard form to write the natural numbers like xyz000000......

Step 1: First of all count the number of digits from left leaving only the first digit.
Step 2: To write it in exponent or standard form, write down the first digit.
Step 3: If there are more digits in the number then put a decimal after the first digit and then write down the other digits until the zero comes. And if there are no digits after the first digit then skip this step.

Step 4: Now place a multiplication sign and then write down the counted digits in the first step as the exponent to the base number 10.

Example: Express 1730000000000 in exponent form.

Sol:  In standard form, the number 1730000000000 will be written as 1.73 x 10¹².

2. Standard form to write decimal numbers like 0.00000.....xyz.

Step 1: First of all count the number of digits from the decimal point to the last digit.

Step 2: If there is only one digit after the zeros then simply write down that digit. Place a multiplication sign and write down the counted digits in step-1 with a negative sign as the exponent to base number 10.

Step 3: If there are two or more non-zero digits at the end of the number. Then, write down the digits followed by a decimal point after the first digit and the other non-zero digits.

Step 4: Now calculate the number of digits in the first step and minus the number of digits appearing after the decimal point.

Step 5: Place a multiplication sign and write down the counted digits in step-4 with a negative sign as an exponent to base number 10.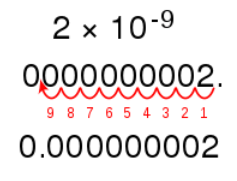

Example: Express 0.000000000000073 in exponent form.

Sol: In standard form, the number will be written as 7.3 x 10^-14.

Comparing Very Large and Very Small Numbers 

To compare the diameters of the Sun and the Earth, we can use their exponential forms.

• The diameter of the Sun is 1.4×10⁹meters.
• The diameter of the Earth is 1.2756×10⁷meters.

To compare these, divide the diameter of the Sun by the diameter of the Earth:

Divide the coefficients and subtract the exponents:

$\frac{1.4}{1.2756}\times 10<sup\; style="font-size:12px\; !important">(</sup>$^9-7)

Calculating the coefficient:

$\frac{1.4}{1.2756}\approx 1.1\backslash frac\{1.4\}\{1.2756\}\; \backslash approx\; 1.1$1
So:

$1.1\times 102\approx 1101.1\; \backslash times\; 10^2\; \backslash approx\; 110$1.1×102≈110

Thus, the diameter of the Sun is approximately 110 times the diameter of the Earth.

$\backslash frac\{1.4\}\{1.2756\}\; \backslash times\; 10^\{(9\; -\; 7)\}$

Example: Compare the two numbers 4.56 × 10⁸ and 392 × 10⁷.

Sol:

Let's compare the two numbers 4.56×10⁸ and 392×10⁷by following the same steps.

First, express both numbers in scientific notation. 

The second number can be rewritten as:

392×10⁷$=3.92\times 10392\times 10$⁹

Now, compare by dividing  4.56×10⁸ and 392×10⁹:

Divide the coefficients and subtract the exponents:

$\frac{4.56}{3.92}\times 10<sup\; style="font-size:12px\; !important">(8-9)</sup>$

Now, calculate the coefficient:

$\frac{4.56}{3.92}$≈1.16
So, the result is:

$1.16\times$10^(-1) =0.116

Thus, 4.56×10⁸ is smaller by about 10 times.

Points to Remember

• Numbers with negative exponents obey the following laws of exponents:

(a) a^m × aⁿ = a^m+n

(b) a^m ÷ aⁿ = a^m-n

(c) (a^m)ⁿ = a^mn

(d) a^m × b^m = (ab)^m

(e) a⁰ = 1

(f) a^m / b^m = (a / b)^m

• Very small numbers can be expressed in standard form using negative exponents.