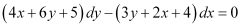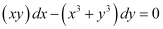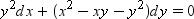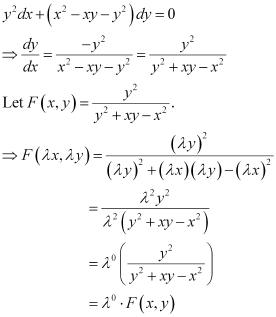Q1: 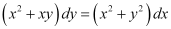
Ans: The given differential equation i.e., (x2 xy) dy = (x2 y2) dx can be written as:
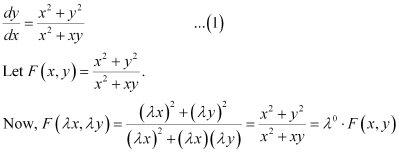
This shows that equation (1) is a homogeneous equation.
To solve it, we make the substitution as: y = vx
Differentiating both sides with respect to x, we get: 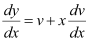
Substituting the values of v and 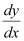 in equation (1), we get:
in equation (1), we get:
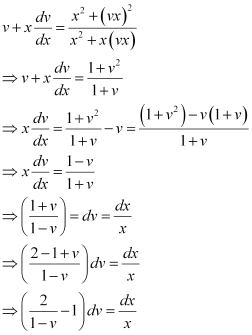
Integrating both sides, we get:
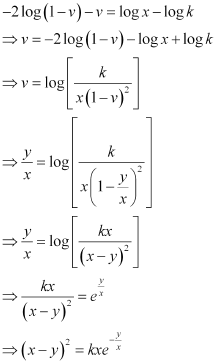
This is the required solution of the given differential equation.
Q2: 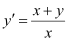
Ans: The given differential equation is:
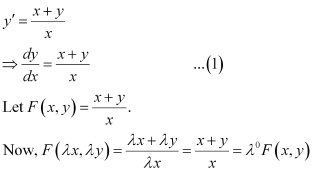
Thus, the given equation is a homogeneous equation.
To solve it, we make the substitution as: y = vx
Differentiating both sides with respect to x, we get: 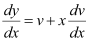
Substituting the values of y and 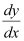 in equation (1), we get:
in equation (1), we get:
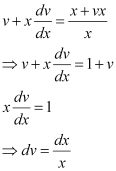
Integrating both sides, we get:
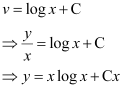
This is the required solution of the given differential equation.
Q3: 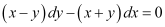
Ans: The given differential equation is:
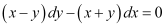
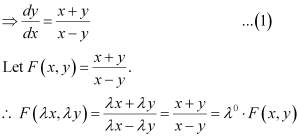
Thus, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as:
y = vx

Substituting the values of y and 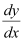 in equation (1), we get:
in equation (1), we get:
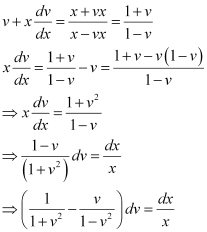
Integrating both sides, we get:
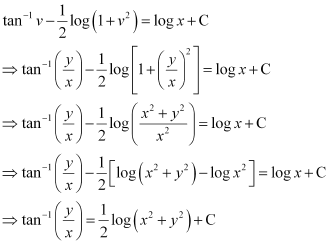
This is the required solution of the given differential equation.
Q4: 
Ans: The given differential equation is:

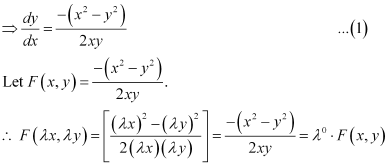
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as: y = vx

Substituting the values of y and 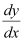 in equation (1), we get:
in equation (1), we get:
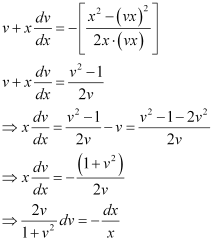
Integrating both sides, we get:
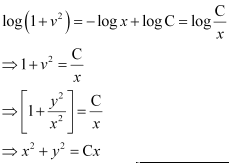
This is the required solution of the given differential equation.
Q5: 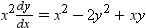
Ans: The given differential equation is:
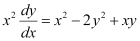
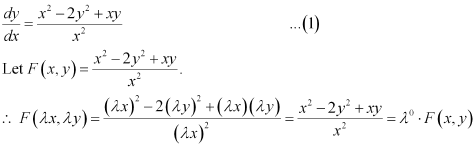
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as: y = vx
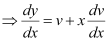
Substituting the values of y and 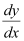 in equation (1), we get:
in equation (1), we get:
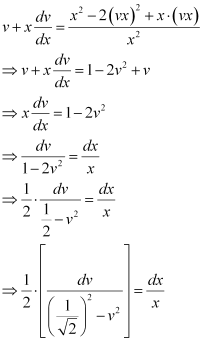
Integrating both sides, we get:
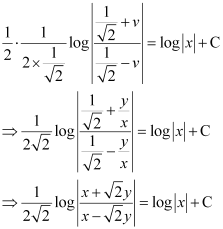
This is the required solution for the given differential equation.
Q6: 
Ans:
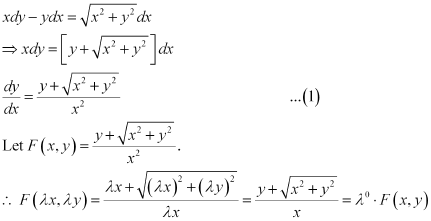
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as:
y = vx
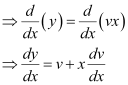
Substituting the values of v and 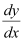 in equation (1), we get:
in equation (1), we get:
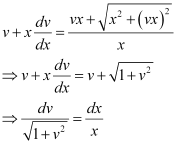
Integrating both sides, we get:
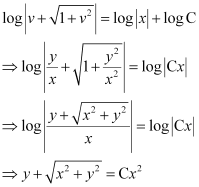
This is the required solution of the given differential equation.
Q7: 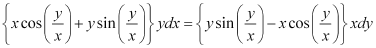
Ans: The given differential equation is:
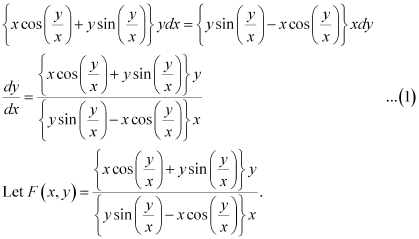
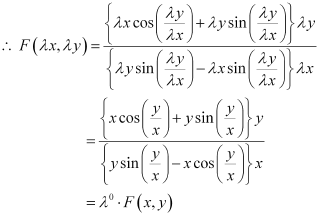
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as:
y = vx
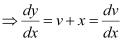
Substituting the values of y and 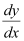 in equation (1), we get:
in equation (1), we get:
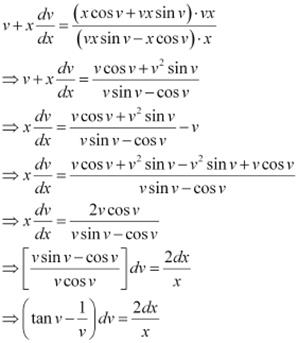
Integrating both sides, we get:
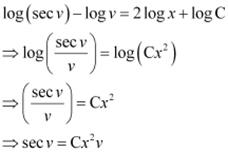
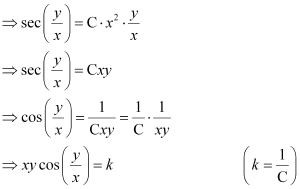
This is the required solution of the given differential equation.
Q8: 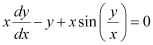
Ans:
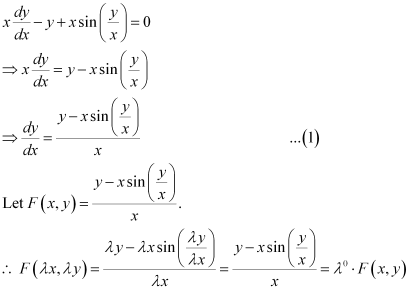
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as:
y = vx
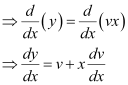
Substituting the values of y and 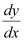 in equation (1), we get:
in equation (1), we get:
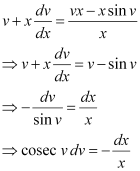
Integrating both sides, we get:
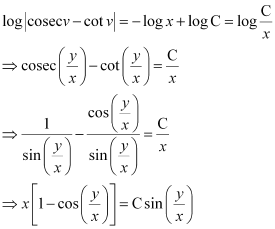
This is the required solution of the given differential equation.
Q9: 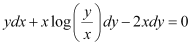
Ans:
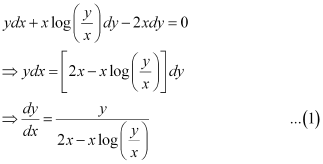
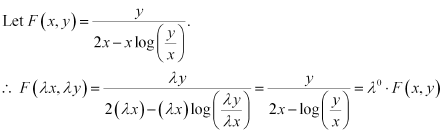
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as: y = vx
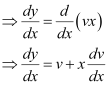
Substituting the values of y and  in equation (1), we get:
in equation (1), we get:
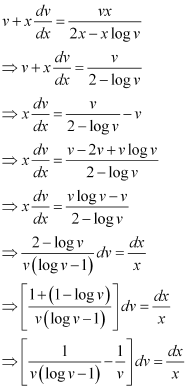
Integrating both sides, we get:
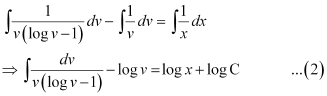
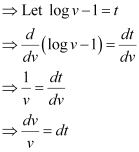
Therefore, equation (1) becomes:
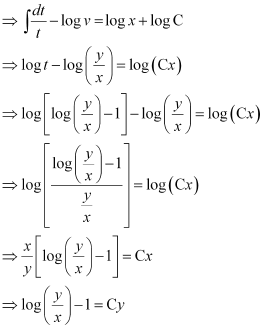
This is the required solution of the given differential equation.
Q10: 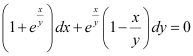
Ans:
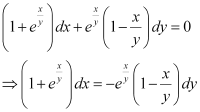
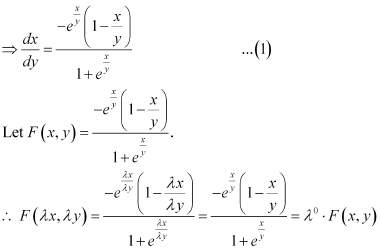
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as:
x = vy
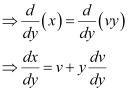
Substituting the values of x and 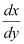 in equation (1), we get:
in equation (1), we get:
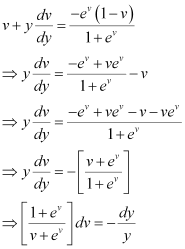
Integrating both sides, we get:
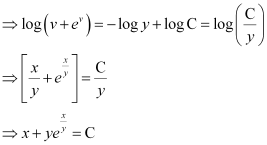
This is the required solution of the given differential equation.
Q11: 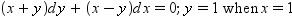
Ans:
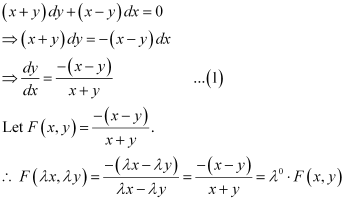
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as:
y = vx
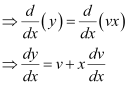
Substituting the values of y and 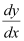 in equation (1), we get:
in equation (1), we get:
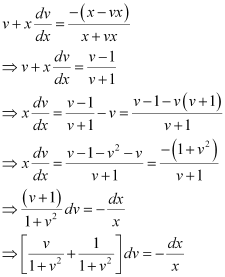
Integrating both sides, we get:
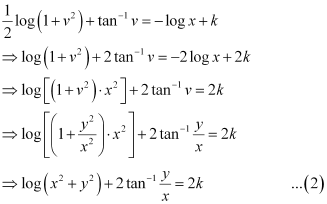
Now, y = 1 at x = 1.
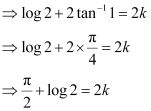
Substituting the value of 2k in equation (2), we get:
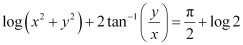
This is the required solution of the given differential equation.
Q12: 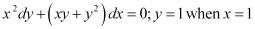
Ans:
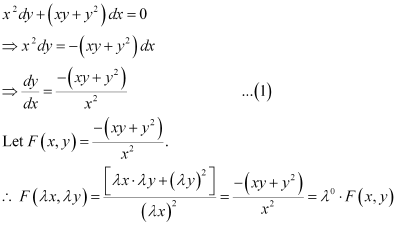
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as: y = vx
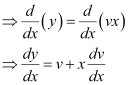
Substituting the values of y and 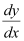 in equation (1), we get:
in equation (1), we get:
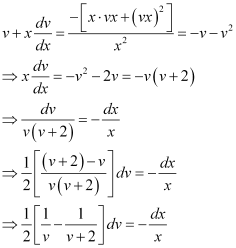
Integrating both sides, we get:
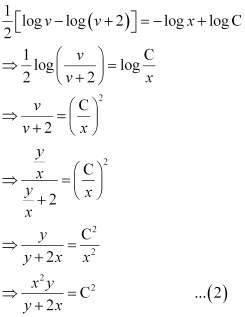
Now, y = 1 at x = 1.

Substituting 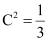 in equation (2), we get:
in equation (2), we get:
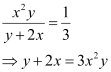
This is the required solution of the given differential equation.
Q13: 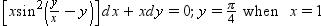
Ans:
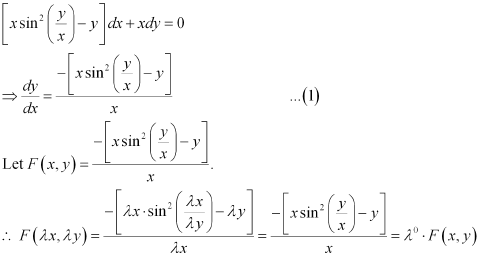
Therefore, the given differential equation is a homogeneous equation.
To solve this differential equation, we make the substitution as:
y = vx
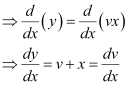
Substituting the values of y and  in equation (1), we get:
in equation (1), we get:

Integrating both sides, we get:
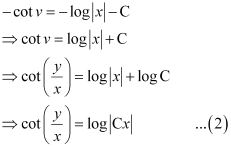
Now, 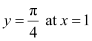 .
.
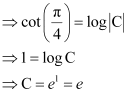
Substituting C = e in equation (2), we get:
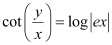
This is the required solution of the given differential equation.
Q14: 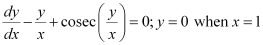
Ans:
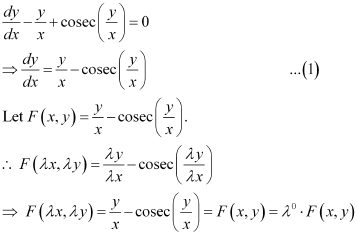
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as:
y = vx
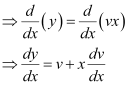
Substituting the values of y and  in equation (1), we get:
in equation (1), we get:

Integrating both sides, we get:
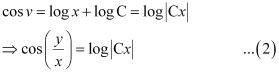
This is the required solution of the given differential equation.
Now, y = 0 at x = 1.
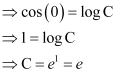
Substituting C = e in equation (2), we get:
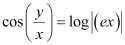
This is the required solution of the given differential equation.
Q15: 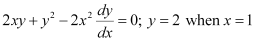
Ans:
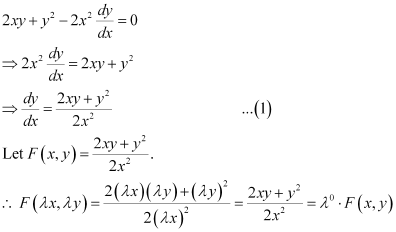
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as:
y = vx
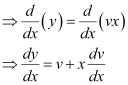
Substituting the value of y and  in equation (1), we get:
in equation (1), we get:
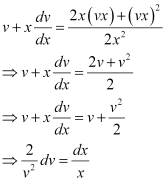
Integrating both sides, we get:
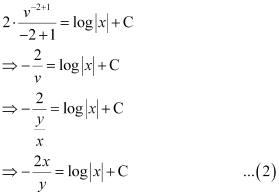
Now, y = 2 at x = 1.
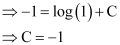
Substituting C = –1 in equation (2), we get:

This is the required solution of the given differential equation.
Q16: A homogeneous differential equation of the form 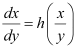 can be solved by making the substitution
can be solved by making the substitution
A. y = vx
B. v = yx
C. x = vy
D. x = v
Ans: For solving the homogeneous equation of the form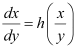 , we need to make the substitution as x = vy.Hence, the correct answer is C.
, we need to make the substitution as x = vy.Hence, the correct answer is C.
Q17: Which of the following is a homogeneous differential equation?
A. 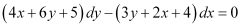
B. 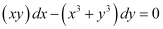
C. 
D. 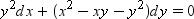
Ans: Function F(x, y) is said to be the homogenous function of degree n, if
F(λx, λy) = λn F(x, y) for any non-zero constant (λ).
Consider the equation given in alternativeD:
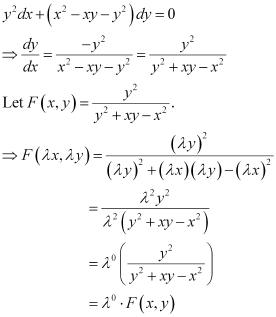
Hence, the differential equation given in alternative D is a homogenous equation.
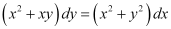
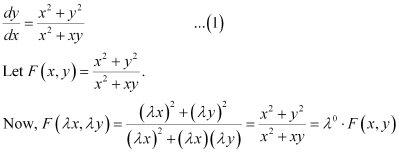
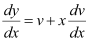
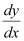 in equation (1), we get:
in equation (1), we get: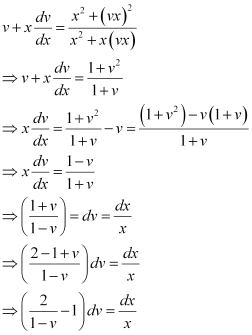
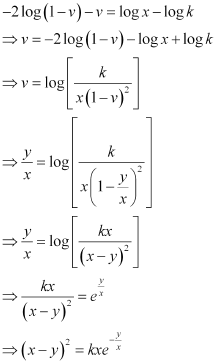
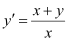
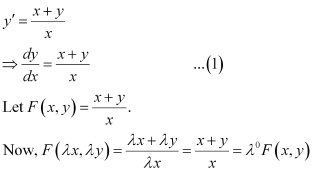
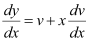
 in equation (1), we get:
in equation (1), we get: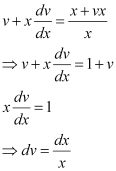
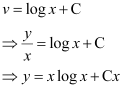
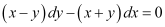
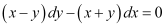
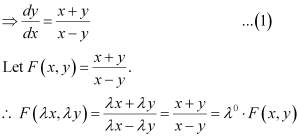

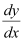 in equation (1), we get:
in equation (1), we get: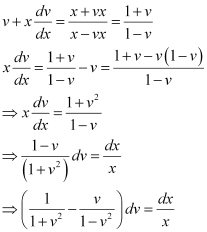
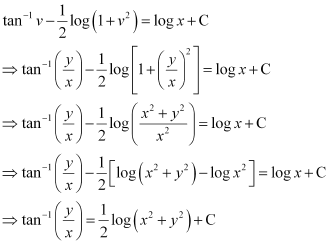


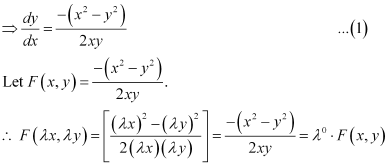

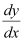 in equation (1), we get:
in equation (1), we get: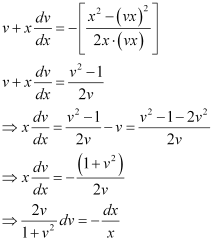
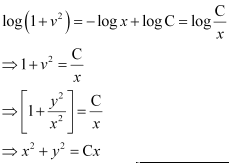
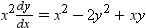
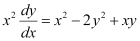
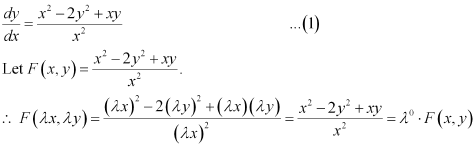
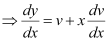
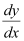 in equation (1), we get:
in equation (1), we get: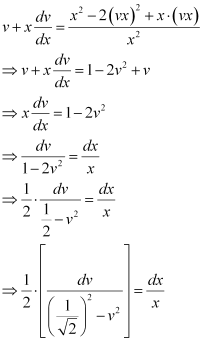
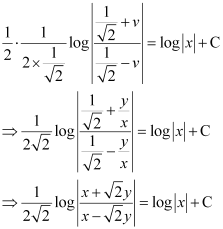

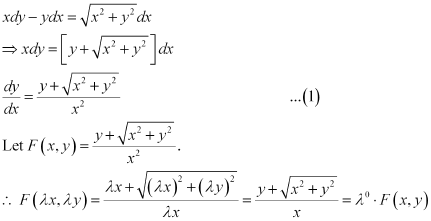
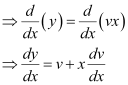
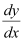 in equation (1), we get:
in equation (1), we get: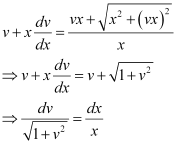
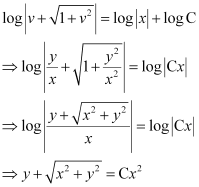
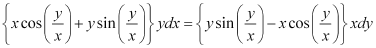
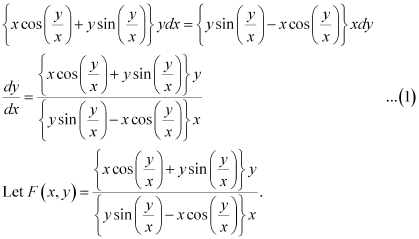
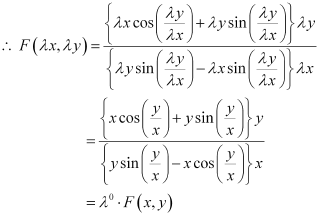
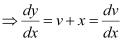
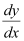 in equation (1), we get:
in equation (1), we get: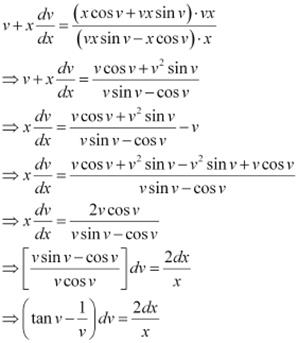
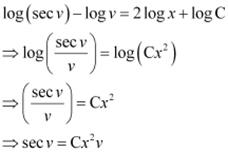
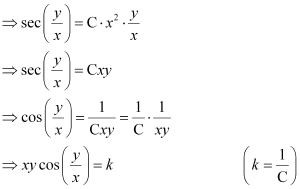
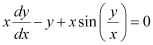
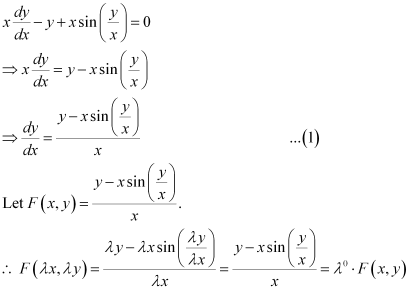
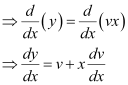
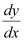 in equation (1), we get:
in equation (1), we get: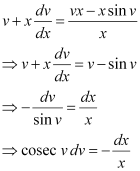
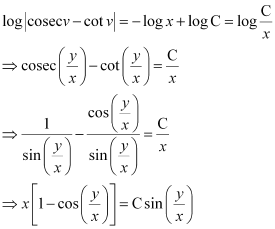
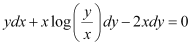
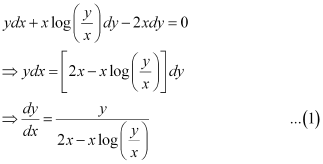
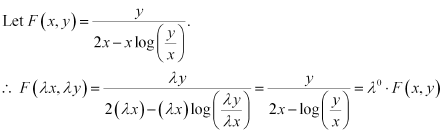
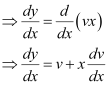
 in equation (1), we get:
in equation (1), we get: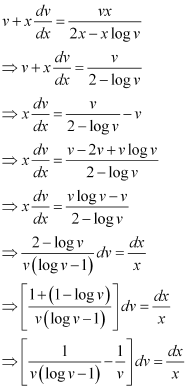
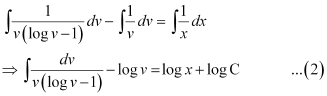
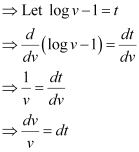
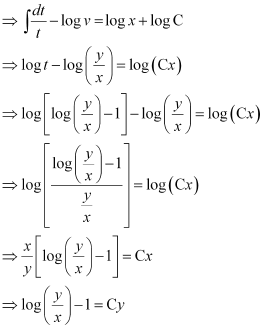
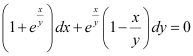
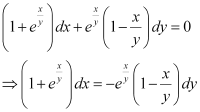
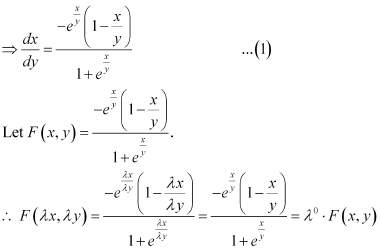
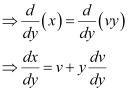
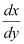 in equation (1), we get:
in equation (1), we get: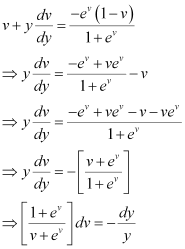
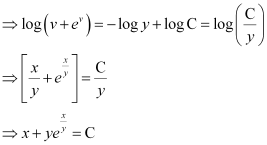
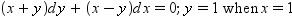
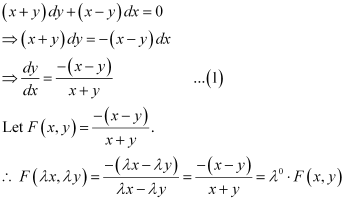
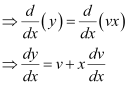
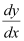 in equation (1), we get:
in equation (1), we get: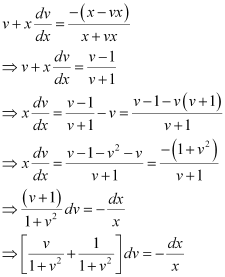
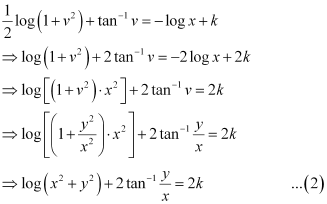
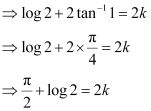
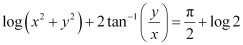
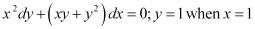
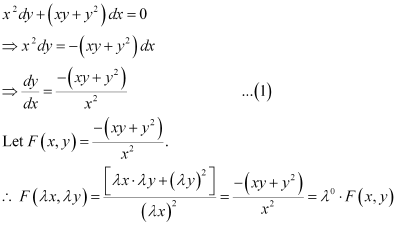
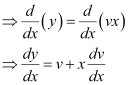
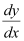 in equation (1), we get:
in equation (1), we get: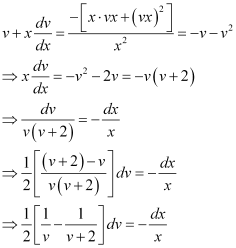
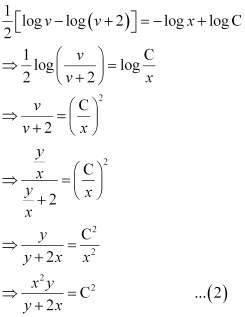

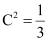 in equation (2), we get:
in equation (2), we get: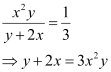
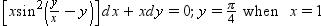
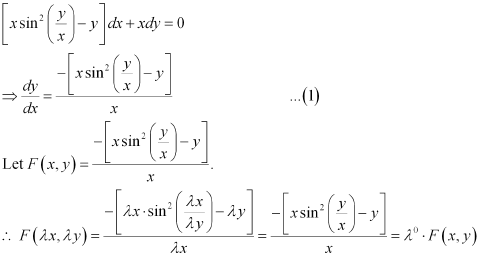
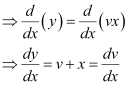
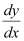 in equation (1), we get:
in equation (1), we get:
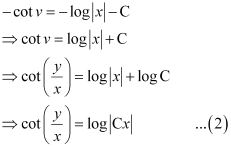
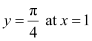 .
.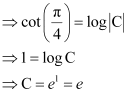
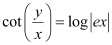
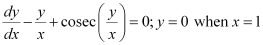
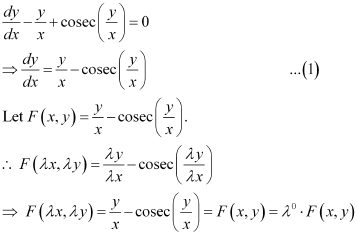
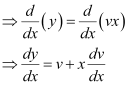
 in equation (1), we get:
in equation (1), we get:
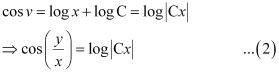
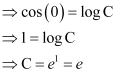
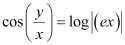
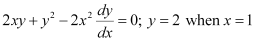
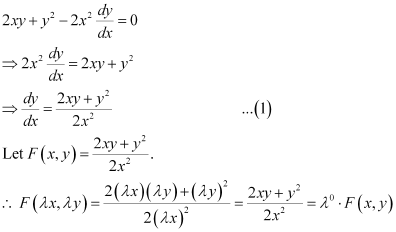
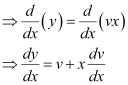
 in equation (1), we get:
in equation (1), we get: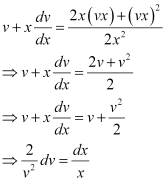
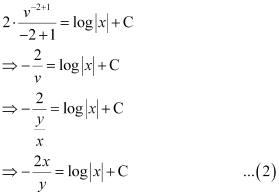
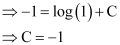

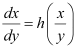 can be solved by making the substitution
can be solved by making the substitution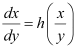 , we need to make the substitution as x = vy.Hence, the correct answer is C.
, we need to make the substitution as x = vy.Hence, the correct answer is C.