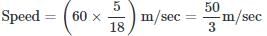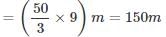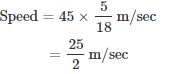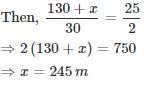Problems on Trains Tips and Tricks for Government Exams
| Table of contents |

|
| Introduction |

|
| Formulas Used |

|
| Types of Train Problems |

|
| Things to Remember |

|
| Solved Examples |

|
Introduction
- Similar to the concept of speed, distance and time, Train problems are specifically based on evaluating the speed, distance covered, and time taken by a train under different conditions.
- There are specific formulas that are to be used to find answers to the train-based questions, and candidates must memorise them in order to crack the answers for problems on trains.

Formulas Used
1. Speed of the Train 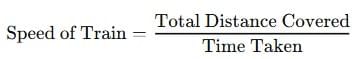
2. Two Trains Moving in Opposite Directions
If the length of two trains is given, say a and b, and the trains are moving in opposite directions with speeds of x and y respectively, then 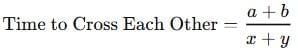
3. Two Trains Moving in the Same Direction
If the length of two trains is given, say a and b, and they are moving in the same direction, with speeds x and y respectively, then
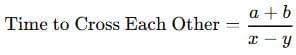
4. Ratio of Speeds Using Time After Crossing
When the starting time of two trains is the same from x and y towards each other, and after crossing each other, they take t1 and t2 time in reaching y and x respectively, then
Ratio between the speed of two trains = √t2: √t1
5. Meeting Point from Station X
If two trains leave x and y stations at times t1 and t2 respectively and travel with speeds L and M respectively, then the distance from x, where the two trains meet, is = 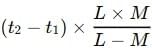
6. Rest Time per Hour
The average speed of a train without any stoppage is x, and with the stoppage, it covers the same distance at an average speed of y, then Rest Time per hour = 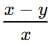
7. Crossing Time for Equal Length Trains (Opposite Directions)
If two trains of equal length and different speeds take t1 and t2 time to cross a pole, then the time taken by them to cross each other if the train is moving in the opposite direction = 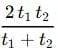
8.Crossing Time for Equal Length Trains (Same Direction)
If two trains of equal lengths and different speeds take t1 and t2 time to cross a pole, then the time taken by them to cross each other if the train is moving in the same direction = 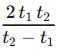
Types of Train Problems
1. Crossing a Stationary Object
- Concept: Train covers only its own length.
- Example: A 150 m train at 54 km/h crosses a pole. Calculate the time taken by it to pass the pole.
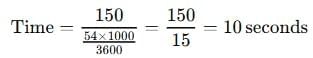
2. Crossing Another Train / Platform
Concept: Train covers the sum of lengths; relative speed depends on direction.
Example: Two trains (100 m at 36 km/h, 200 m at 54 km/h) moving in opposite directions. Calculate time taken to cross each other
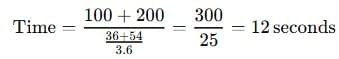
3. Equation-Based Problems
Concept: Information from two cases is used to form equations.
Example: A train crosses a pole in 8 seconds and a platform of 160 m in 24 seconds. Find train length and speed.
Sol: Let the train length = L, and speed = S.
From pole:
L ÷ S = 8 ⟹ L = 8S
From platform:
(L + 160) ÷ S = 24
Substituting L = 8S:
(8S + 160) ÷ S = 24
⟹ 8S + 160 = 24S
⟹ 16S = 160
⟹ S = 10 m/s = 36 km/h
Thus, L = 80 m.
Things to Remember
1. Always remember the two objects
Train vs pole/man → distance = length of train
Train vs platform → distance = length of train + length of platform
Train vs train → distance = sum of train lengths
2. Relative speed matters
Opposite directions → add speeds
Same direction → subtract speeds
3. Always remember the conversions
- 1 km/hr = 5/18 m/s
- 1m/s = 18/5 km/hr
Solved Examples
|
66 videos|260 docs
|
FAQs on Problems on Trains Tips and Tricks for Government Exams
| 1. What are the basic concepts involved in solving train problems? |  |
| 2. How do you calculate the time taken for two trains to cross each other? |  |
| 3. What is the role of length in train problems, and how is it used in calculations? |  |
| 4. Can you explain how to approach problems involving trains moving in opposite directions? |  |
| 5. What strategies can be used to solve complex train problems efficiently? |  |