Minimization of Boolean Functions | Digital Logic - Computer Science Engineering (CSE) PDF Download
This process in which we simplify the given algebraic expression present in a boolean expression is known as minimization. This minimization is very crucial since it helps us in the reduction of cost and the overall complexity of an associated circuit.
For instance, the function F = x’y’z +x’yz + xy’ can be minimized to F = x’z + xy’. Here are the circuits that are associated with the expressions given above –
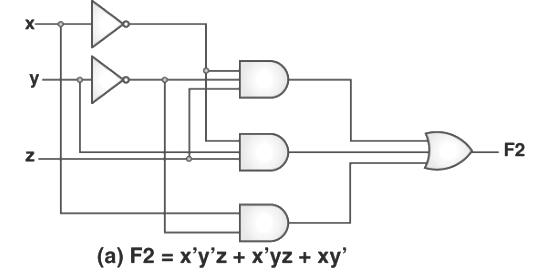
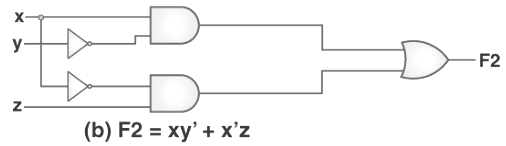
It is very clear from the image given above that the minimized version of any expression requires comparatively lesser numbers of logic gates. It also substantially reduces the overall complexity of the circuit. Hence, minimization is very important to discover the most economical form of equivalent representation of a given boolean function. We can perform minimization using the K-Map method or Algebraic Manipulation. Every method has its own pros and cons.
Minimization using Algebraic Manipulation
Out of all the methods that we use for the process of minimization, this method is the simplest. It is the most suitable for any medium-sized expression that involves 4 or 5 variables in total. Remember that algebraic manipulation is basically a manual method. And thus, it is very much prone to blunders and human error.
Here are the Common Laws that we use in the process of algebraic manipulation:
A + A’ = 1
A + A’B = A +B
A + AB = A
Example 1: Let us minimize the boolean function given as follows using the method of algebraic manipulation-
F = ABC’D’ + ABC’D + AB’C’D + ABCD + AB’CD + ABCD’ + AB’CD’
The properties used here refer to the 3 most common laws mentioned above.
F = ABC’ (D’ + D) + AB’C’D + ACD (B + B’) + ACD’ (B + B’)
= ABC’ + AB’C’D + ACD + ACD’ Using Property- 1
= ABC’ + AB’C’D + AC (D + D’)
= ABC’ + AB’C’D + AC Using Property-1
= A (BC’ + C) + AB’C’D
= A (B +C) + AB’C’D Using Property-2
= AB + AC + AB’C’D
= AB + AC + AC’D Using Property-2
= AB + AC + AD Using Property-2
Minimization Using K-Map
The method of algebraic manipulation, as we witnessed above, is pretty long, cumbersome, and tedious to follow for every expression. Instead, we can use the K-Map method, which is much faster. It can be used to solve the Boolean Functions up to five variables. You can learn more about K-Map by visiting here.
Example 2: Let us consider the same expression that we have used in example-1 and then minimize it using the K-Map method instead of the algebraic manipulation method.
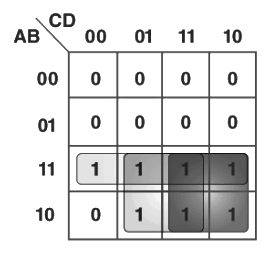
A K-Map of 4 variables of the expression is given here:
The figure given above highlights the prime implicants here in red, green, and blue.
The blue one extends to 4 squares, and it gives us – AC
The red one extends to 4 squares, and it gives us – AD
The green one extends to the whole third row, and it gives us – AB
Thus, the minimized Boolean expression would be – AB + AC + AD
|
53 docs|15 tests
|
FAQs on Minimization of Boolean Functions - Digital Logic - Computer Science Engineering (CSE)
| 1. What is the purpose of minimizing Boolean functions in computer science? |  |
| 2. What are the common methods used for minimizing Boolean functions? |  |
| 3. How does a Karnaugh Map work for minimizing Boolean functions? |  |
| 4. What is the Quine-McCluskey algorithm, and when is it used? |  |
| 5. Why is it important to minimize Boolean functions in digital design? |  |