Important Straight Lines & Pair of Straight Lines Formulas for JEE and NEET
1. Distance Formula :
- The distance between the points A(x1,y1) and B(x2,y2) is
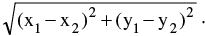
2. Section Formula :
- If P(x,y) divides the line joining A(x1,y1) & B(x2,y2) in the ratio m : n, then ;
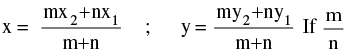 is positive, the division is internal, but if
is positive, the division is internal, but if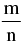 is negative, the division is external.
is negative, the division is external. - Note : If P divides AB internally in the ratio m : n & Q divides AB externally in the ratio m : n then P & Q are said to be harmonic conjugate of each other w.r.t. AB.
- Mathematically ;
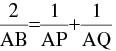 i.e. AP, AB & AQ are in H.P.
i.e. AP, AB & AQ are in H.P.
3. Centroid And Incentre :
- If A(x1, y1), B(x2, y2), C(x3, y3) are the vertices of triangle ABC, whose sides BC, CA, AB are of lengths a, b, c respectively, then the coordinates of the centroid are :
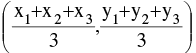 & the coordinates of the incentre are :
& the coordinates of the incentre are : 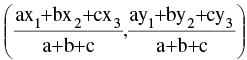
- Note that incentre divides the angle bisectors in the ratio (b + c) : a ; (c + a) : b & (a + b) : c.
- Remember :
(i) Orthocentre, Centroid & circumcentre are always collinear & centroid divides the line joining orthocentre & cercumcentre in the ratio 2 : 1 .
(ii) In an isosceles triangle G, O, I & C lie on the same line .
4. Slope Formula :
- If θ is the angle at which a straight line is inclined to the positive direction of x−axis, & 0° < q < 180°, θ ≠ 90°, then the slope of the line, denoted by m, is defined by m = tan θ. If θ is 90°, m does not exist, but the line is parallel to the y−axis.If θ = 0, then m = 0 & the line is parallel to the x−axis.
- If A (x1, y1) & B (x2, y2), x1≠ x2, are points on a straight line, then the slope m of the line is given by: m =
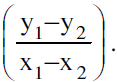
5. Condition Of Collinearity Of Three Points −(Slope Form) :
- Points A (x1, y1), B (x2, y2), C(x3, y3) are collinear if
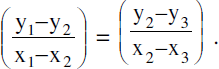
6. Equation Of A Straight Line In Various Forms :
- Slope − intercept form: y = mx + c is the equation of a straight line whose slope is m & which makes an intercept c on the y−axis .
- Slope one point form: y − y1 = m (x − x1) is the equation of a straight line whose slope is m & which passes through the point (x1, y1)
- Parametric form : The equation of the line in parametric form is given by
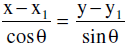 = r (say). Where ‘r’ is the distance of any point (x , y) on the line from the fixed point (x1, y1) on the line. r is positive if the point (x, y) is on the right of (x1, y1) and negative if (x,y) lies on the left of (x1, y1) .
= r (say). Where ‘r’ is the distance of any point (x , y) on the line from the fixed point (x1, y1) on the line. r is positive if the point (x, y) is on the right of (x1, y1) and negative if (x,y) lies on the left of (x1, y1) . - Two point form :
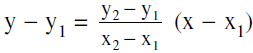 is the equation of a straight line which passes through the points (x1, y1) & (x2, y2)
is the equation of a straight line which passes through the points (x1, y1) & (x2, y2) - Intercept form :
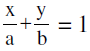 is the equation of a straight line which makes intercepts a & b on OX & OY respectively .
is the equation of a straight line which makes intercepts a & b on OX & OY respectively . - Perpendicular form : xcos α + ysin α = p is the equation of the straight line where the length of the perpendicular from the origin O on the line is p and this perpendicular makes angle α with positive side of x−axis .
- General Form : ax + by + c = 0 is the equation of a straight line in the general form
7. Position Of The Point (X1, Y1) Relative To The Line ax + by + C = 0 :
- If ax1 + by1 + c is of the same sign as c, then the point (x1, y1) lie on the origin side of ax + by + c = 0.
- But if the sign of ax1 + by1 + c is opposite to that of c, the point (x, y1) will lie on the non-origin side of ax + by + c = 0.
8. The Ratio In Which A Given Line Divides The Line Segment Joining Two Points :
- Let the given line ax + by + c = 0 divide the line segment joining A(x1, y1) & B(x2, y2) in the ratio m : n, then
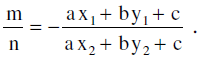
- If A & B are on the same side of the given line then
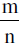 is negative but if A & B are on opposite sides of the given line , then
is negative but if A & B are on opposite sides of the given line , then 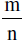 is positive.
is positive.
9. Length Of Perpendicular From A Point On A Line :
- The length of perpendicular from P(x1, y1) on ax + by + c = 0 is
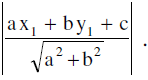
10. Angle Between Two Straight Lines In Terms Of Their Slopes :
- If m1 & m2 are the slopes of two intersecting straight lines (m1 m2 ≠ −1) & q is the acute angle between them, then tan θ =
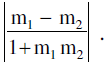
- Note : Let m1, m2, m3 are the slopes of three lines L1 = 0 ; L2 = 0 ; L3 = 0 where m1 > m2 > m3 then the interior angles of the D ABC found by these lines are given by,
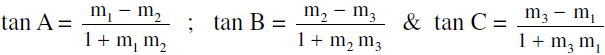
11. Parallel Lines :
- When two straight lines are parallel their slopes are equal. Thus any line parallel to ax + by + c = 0 is of the type ax + by + k = 0 . Where k is a parameter.
- The distance between two parallel lines with equations ax + by + c1 = 0 & ax + by + c2 =
 Note that the coefficients of x & y in both the equations must be same.
Note that the coefficients of x & y in both the equations must be same. - The area of the parallelogram =
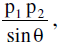 where p1 & p2 are distances between two pairs of opposite sides & θ is the angle between any two adjacent sides . Note that area of the parallelogram bounded by the lines y = m1x + c1, y = m1x + c2 and y = m2x + d1 , y = m2x + d2 is given by
where p1 & p2 are distances between two pairs of opposite sides & θ is the angle between any two adjacent sides . Note that area of the parallelogram bounded by the lines y = m1x + c1, y = m1x + c2 and y = m2x + d1 , y = m2x + d2 is given by 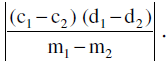
12. Perpendicular Lines :
- When two lines of slopes m1& m2 are at right angles, the product of their slopes is −1, i.e. m1 m2 = −1. Thus any line perpendicular to ax + by + c = 0 is of the form bx − ay + k = 0, where k is any parameter.
- The lines ax + by + c = 0 & a' x + b' y + c' = 0 are right angles if & only if aa' + bb' = 0.
13. Equations of straight lines through (x1 , y1) making angle α with y = mx + c are:
- (y − y1) = tan (θ − α) (x − x1)
- (y − y1) = tan (θ + α) (x − x1) , where tan q = m.
14. Condition Of Concurrency :
- Three lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 & a3x + b3y + c3 = 0 are concurrent if
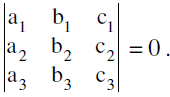
- Alternatively : If three constants A, B & C can be found such that A(a1x + b1y + c1) + B(a2x + b2y + c2) + C(a3x + b3y + c3) = 0 , then the three straight lines are concurrent.
15. Area Of A Triangle :
- If (xi, yi), i = 1, 2, 3 are the vertices of a triangle, then its area is equal to
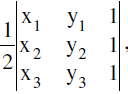 provided the vertices are considered in the counter clockwise sense.
provided the vertices are considered in the counter clockwise sense. - The above formula will give a (−) ve area if the vertices (xi, yi) , i = 1, 2, 3 are placed in the clockwise sense.
16. Condition Of Collinearity Of Three Points−(Area Form):
- The points (xi , yi) , i = 1 , 2 , 3 are collinear if
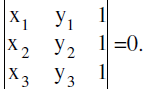
17. The Equation Of A Family Of Straight Lines Passing Through The Points Of Intersection Of Two Given Lines:
- The equation of a family of lines passing through the point of intersection of a1x + b1y + c1 = 0 & a2x + b2y + c2 = 0 is given by (a1x + b1y + c1) + k(a2x + b2y + c2) = 0, where k is an arbitrary real number.
- Note: If u1 = ax + by + c , u2 = a'x + b'y + d , u3 = ax + by + c', u4 = a'x + b'y + d'
then, u1 = 0; u2 = 0; u3 = 0; u4 = 0 form a parallelogram. - u2 u3 − u1 u4 = 0 represents the diagonal BD.
- The diagonal AC is also given by u1 + lu4 = 0 and u2 + μu3 = 0, if the two equations are identical for some λ and μ.
[For getting the values of λ & μ compare the coefficients of x, y & the constant terms]
18. Bisectors Of The Angles Between Two Lines :
- Equations of the bisectors of angles between the lines ax + by + c = 0 &
a'x + b'y + c' = 0 (ab' ≠ a'b) are :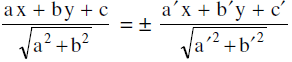
- To discriminate between the acute angle bisector & the obtuse angle bisector
If θ be the angle between one of the lines & one of the bisectors, find tan q .
If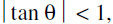 then 2θ < 90° so that this bisector is the acute angle bisector .
then 2θ < 90° so that this bisector is the acute angle bisector .
If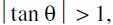 then we get the bisector to be the obtuse angle bisector .
then we get the bisector to be the obtuse angle bisector . - To discriminate between the bisector of the angle containing the origin & that of the angle not containing the origin. Rewrite the equations , ax + by + c = 0 & a'x + b'y + c' = 0 such that the constant terms c , c' are positive.
Then;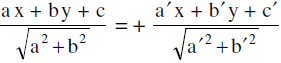 gives the equation of the bisector of the angle containing the origin &
gives the equation of the bisector of the angle containing the origin & 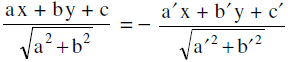 gives the equation of the bisector of the angle not containing the origin.
gives the equation of the bisector of the angle not containing the origin. - To discriminate between acute angle bisector & obtuse angle bisector proceed as follows
Write ax + by + c = 0 & a'x + b'y + c' = 0 such that constant terms are positive .
If aa' + bb' < 0 , then the angle between the lines that contains the origin is acute and the equation of the bisector of this acute angle is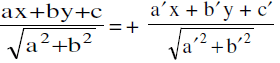
therefore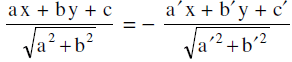 is the equation of other bisector.
is the equation of other bisector.
If, however , aa' + bb' > 0 , then the angle between the lines that contains the origin is obtuse & the equation of the bisector of this obtuse angle is: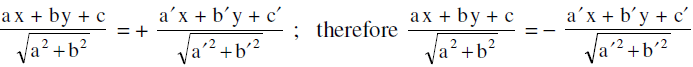
is the equation of other bisector. - Another way of identifying an acute and obtuse angle bisector is as follows :
Let L1 = 0 & L2 = 0 are the given lines & u1 = 0 and u2 = 0 are the bisectors between L1 = 0 & L2 = 0. Take a point P on any one of the lines L1 = 0 or L2 = 0 and drop perpendicular on u1 = 0 & u2 = 0 as shown. If ,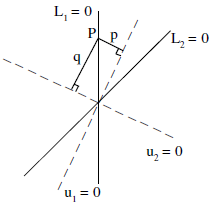
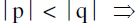 u1 is the acute angle bisector .
u1 is the acute angle bisector .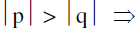 u1 is the obtuse angle bisector .
u1 is the obtuse angle bisector .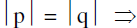 the lines L1 & L2 are perpendicular .
the lines L1 & L2 are perpendicular . - Note : Equation of straight lines passing through P(x1, y1) & equally inclined with the lines a1x + b1y + c1 = 0 & a2x + b2y + c2 = 0 are those which are parallel to the bisectors between these two lines & passing through the point P .
19. A Pair Of Straight Lines Through Origin :
- A homogeneous equation of degree two of the type ax2 + 2hxy + by2 = 0 always represents a pair of straight lines passing through the origin & if :
- h2 > ab ⇒ lines are real & distinct .
- h2 = ab ⇒ lines are coincident .
- h2 < ab ⇒ lines are imaginary with real point of intersection i.e. (0, 0)
- If y = m1x & y = m2x be the two equations represented by ax2 + 2hxy + by2 = 0, then;
m1 + m2 =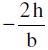 & m1 m2 =
& m1 m2 = 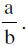
- If θ is the acute angle between the pair of straight lines represented by, ax2 + 2hxy + by2 = 0, then; tan θ =
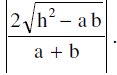 The
The
condition that these lines are:
(a) At right angles to each other is a + b = 0. i.e. co−efficient of x2 + coefficient of y2 =0.
(b) Coincident is h2 = ab.
(c) Equally inclined to the axis of x is h = 0. i.e. coeff. of xy = 0. - Note: A homogeneous equation of degree n represents n straight lines passing through origin.
20. General Equation Of Second Degree Representing A Pair Of Straight Lines:
- ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a pair of straight lines if:
abc + 2fgh − af2 − bg2 − ch2 = 0, i.e. if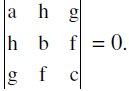
- The angle θ between the two lines representing by a general equation is the same as that between the two lines represented by its homogeneous part only .
21. The joint equation of a pair of straight lines joining origin to the points of intersection of the line given
by lx + my + n = 0 ................ (i) &
the 2nd degree curve : ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 ....... (ii)
is ax2 + 2hxy + by2 + 2gx 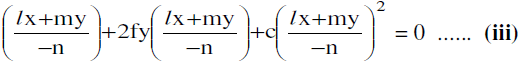
(iii) is obtained by homogenizing (ii) with the help of (i), by writing (i) in the form: 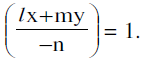
22. The equation to the straight lines bisecting the angle between the straight lines,
ax2 + 2hxy + by2 = 0 is 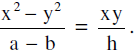
23. The product of the perpendiculars, dropped from (x1, y1) to the pair of lines represented by the equation, ax2 + 2hxy + by2 = 0 is 
24. Any second-degree curve through the four points of intersection of f(x y) = 0 & xy = 0 is given by f (x y) + λ xy = 0 where f(xy) = 0 is also a second-degree curve.
|
176 videos|582 docs|160 tests
|
FAQs on Important Straight Lines & Pair of Straight Lines Formulas for JEE and NEET
| 1. What is the general form of the equation of a straight line? |  |
| 2. How can we determine the slope of a straight line from its equation? |  |
| 3. What are the conditions for two straight lines to be parallel? |  |
| 4. What is a pair of straight lines, and how can they be represented mathematically? |  |
| 5. How do we find the point of intersection of two straight lines? |  |





















