Poisson and Laplace Equations | Physics for IIT JAM, UGC - NET, CSIR NET PDF Download
Introduction
In physics, especially in the field of electrostatics, fluid dynamics, and potential theory, Poisson and Laplace equations play a crucial role in describing how physical quantities like electric potential and gravitational potential behave in a region of space. These partial differential equations are fundamental tools for understanding the distribution of fields and potentials due to sources like charges or masses.
The Poisson equation is generally used when there is a known source of potential, whereas the Laplace equation is a special case where the source is zero. These equations help simplify complex physical systems and allow scientists and engineers to predict how fields and potentials will evolve over space.
A useful approach to the calculation of electric potentials is to relate that potential to the charge density which gives rise to it. The electric field is related to the charge density by the divergence relationship
and the electric field is related to the electric potential by a gradient relationship
Therefore the potential is related to the charge density by Poisson's equation
In a charge-free region of space, this becomes LaPlace's equation
This mathematical operation, the divergence of the gradient of a function, is called the LaPlacian. Expressing the LaPlacian in different coordinate systems to take advantage of the symmetry of a charge distribution helps in the solution for the electric potential V. For example, if the charge distribution has spherical symmetry, you use the LaPlacian in spherical polar coordinates.
Since the potential is a scalar function, this approach has advantages over trying to calculate the electric field directly. Once the potential has been calculated, the electric field can be computed by taking the gradient of the potential.
Potential of a Uniform Sphere of Charge
The use of Poisson's and Laplace's equations will be explored for a uniform sphere of charge. In spherical polar coordinates, Poisson's equation takes the form:
but since there is full spherical symmetry here, the derivatives with respect to θ and φ must be zero, leaving the form
Examining first the region outside the sphere, Laplace's law applies.
Since the zero of potential is arbitrary, it is reasonable to choose the zero of potential at infinity, the standard practice with localized charges. This gives the value b=0. Since the sphere of charge will look like a point charge at large distances, we may conclude that
so the solution to LaPlace's law outside the sphere is
Now examining the potential inside the sphere, the potential must have a term of order r2 to give a constant on the left side of the equation, so the solution is of the form
Substituting into Poisson's equation gives
Now to meet the boundary conditions at the surface of the sphere, r = R
The full solution for the potential inside the sphere from Poisson's equation is
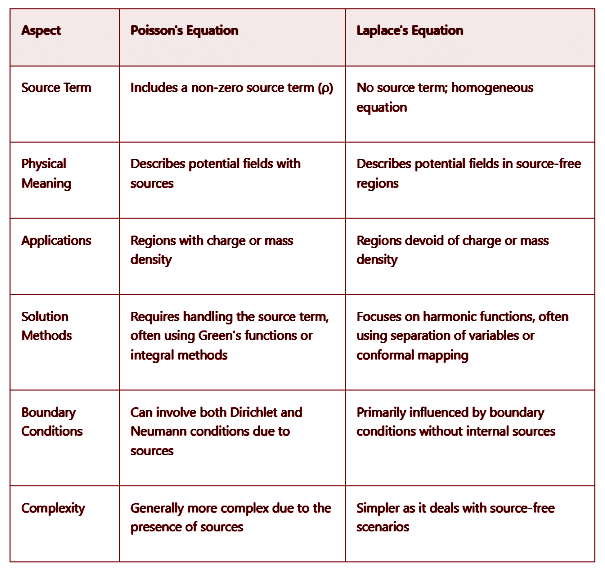
Difference Between Poisson's and Laplace's Equations
FAQs on Poisson and Laplace Equations - Physics for IIT JAM, UGC - NET, CSIR NET
| 1. What is the potential of a uniform sphere of charge at a point outside the sphere? |  |
| 2. How does the potential behave inside a uniform sphere of charge? |  |
| 3. What is the difference between Poisson's and Laplace's equations in electrostatics? |  |
| 4. When should Poisson's equation be used instead of Laplace's equation? |  |
| 5. How do boundary conditions affect the solutions to Poisson's and Laplace's equations? |  |
















