Definition of a Matrix - Matrices and Determinants, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com PDF Download
What is a Matrix?
This lesson introduces the matrix - the rectangular array at the heart of matrix algebra. Matrix algebra is used quite a bit in advanced statistics, largely because it provides two benefits.
- Compact notation for describing sets of data and sets of equations.
- Efficient methods for manipulating sets of data and solving sets of equations.
Matrix Definition
A matrix is a rectangular array of numbers arranged in rows and columns. The array of numbers below is an example of a matrix.
The number of rows and columns that a matrix has is called its dimension or its order. By convention, rows are listed first; and columns, second. Thus, we would say that the dimension (or order) of the above matrix is 3 x 4, meaning that it has 3 rows and 4 columns.
Numbers that appear in the rows and columns of a matrix are called elements of the matrix. In the above matrix, the element in the first column of the first row is 21; the element in the second column of the first row is 62; and so on.
Matrix Notation
Statisticians use symbols to identify matrix elements and matrices.
Matrix elements. Consider the matrix below, in which matrix elements are represented entirely by symbols.
- By convention, first subscript refers to the row number; and the second subscript, to the column number. Thus, the first element in the first row is represented by A11. The second element in the first row is represented by A12. And so on, until we reach the fourth element in the second row, which is represented byA24.
Matrices. There are several ways to represent a matrix symbolically. The simplest is to use a boldface letter, such as A, B, or C. Thus, A might represent a 2 x 4 matrix, as illustrated below.
Another approach for representing matrix A is:
A = [ Aij ] where i = 1, 2 and j = 1, 2, 3, 4
This notation indicates that A is a matrix with 2 rows and 4 columns. The actual elements of the array are not displayed; they are represented by the symbol Aij.
Other matrix notation will be introduced as needed. For a description of all the matrix notation used in this tutorial, see the Matrix Notation Appendix.Matrix Equality
To understand matrix algebra, we need to understand matrix equality. Two matrices are equal if all three of the following conditions are met:
- Each matrix has the same number of rows.
- Each matrix has the same number of columns.
- Consider the three matrices shown below.
- Corresponding elements within each matrix are equal.
If A = B, we know that x = 222 and y = 333; since corresponding elements of equal matrices are also equal. And we know that matrix C is not equal to A or B, because C has more columns than A or B.Test Your Understanding
Problem 1
The notation below describes two matrices - matrix A and matrix B.
A = [ Aij ]
where i = 1, 2, 3 and j = 1, 2
Which of the following statements about A and B are true?
I. Matrix A has 5 elements.
II. The dimension of matrix B is 4 x 2.
III. In matrix B, element B21 is equal to 222.(A) I only
(B) II only
(C) III only
(D) All of the above
(E) None of the aboveSolution
The correct answer is (E).
Matrix A has 3 rows and 2 columns; that is, 3 rows, each with 2 elements. This adds up to 6 elements, altogether - not 5.- The dimension of matrix B is 2 x 4 - not 4 x 2. That is, matrix B has 2 rows and 4 columns - not 4 rows and 2 columns.
- And, finally, element B21 refers to the first element in the second row of matrix B, which is equal to 555 - not 222.
Example: Types of Matrices
Q1: Let A and B be two square matrices of same order. If AB is a null matrix, then which one of the following is correct?
(a) Both A and B are null matrices
(b) Either A or B is a null matrix
(c) B is a null matrix if A is a nonsingular matrix
(d) Both A and B are singular matrices
Ans: (c)
Sol:
Given AB = O
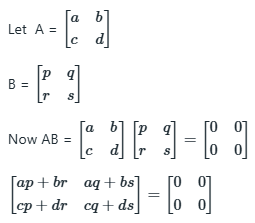
Comparing both sides, we get
⇒ ap + br = 0...(1)
⇒ aq + bs = 0...(2)
⇒ cp + dr = 0...(3)
⇒ cq + ds = 0...(4)
From Eqs. (i) and (iii), we get:
⇒ (ad – bc)p = 0 and (ad – bc)r = 0
From Eqs. (ii) and (iv), we get:
⇒ (ad – bc) q = 0 and (ad – bc)s = 0
Now, if A is non-singular
ad – bc ≠ 0
So p = q = r = s = 0.
Then, B is the null matrix.
∴ Option (c) is correct.
Q2: A, B, C, D are square matrices such that A + B is symmetric, A - B is skew-symmetric, and D is the transpose of C. If 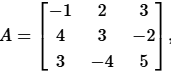 and
and 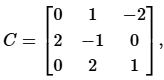 then the matrix B + D =
then the matrix B + D =
(a) 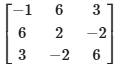
(b) 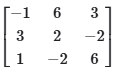
(c) 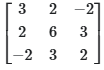
(d) 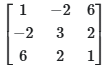
Ans: (b)
Sol:
Concept
(A + B)T = A + B (symmetric)
(A - B)T = - (A - B) (skew-symmetric)
Calculation
Given:
A + B is symmetric, A - B is skew-symmetric, D = CT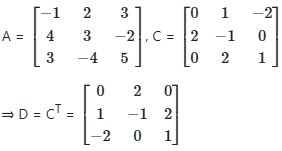
AT + BT = A + B ...(1)
AT - BT = -A + B ...(2)
⇒ (1) + (2): 2AT = 2B
⇒ B = AT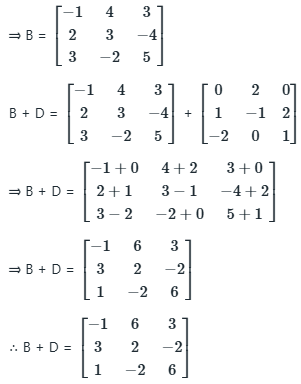
Hence option b is correct
Q3: If A and B are matrices of same order, then (AB' – BA') is a
(a) Diagonal matrix.
(b) symmetric matrix
(c) unit matrix
(d) skew-symmetric matrix
Ans: (d)
Sol:
Given:
Two matrices A and B of same order is given.
Concept Used:
A' = A, then A will be a symmetric matrix,
A' = - A, then A will be a skew- symmetric matrix.
Calculations:
We have,
(AB' - BA') if we calculate (AB' - BA')'
⇒ (AB' - BA')' = (AB')' - (BA')'
⇒ (AB' - BA')' = (B')' A' - (A')' B' {(AB)' = B'A'}
⇒ (AB' - BA')" = B A' - A B' {(A')' = A}
⇒ (AB' - BA')' = - (AB' - BA')
Hence (AB' - BA') is skew-symmetric matrix.
∴ Option d is correct.
Q4: If A is a square matrix such that A2 = I, then A3 + (A + I)2 - 9A - I2 - A2 is
(a) -10A
(b)10A
(c) -6A
(d) 6A
Ans: (c)
Sol:
Concept:
Properties of identity matrix:
If A is the square matrix of order n × n
AI = IA = A
In = I (Where n ∈ N)
Calculation:
Given
A2 = I
Now, A3 + (A + I)2 - 9A - I2 - A2
= A2. A + A2 + I2 + 2AI - 9A - I2 - A2
= I. A + I + I + 2AI - 9A - I - I [∵ A2 = I and AI = IA = A]
= AI + 2AI - 9A
= 3AI - 9A
= 3A - 9A
= - 6A
Q5: The matrix 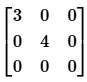 is a
is a
(a) identity matrix
(b) symmetric matrix
(c) skew symmetric matrix
(d) none of these
Ans: (b)
Sol:
Concept:
A square matrix A = [aij]n × n is said to be symmetric if AT = A
AT (Transpose) is obtained by changing rows to columns and columns to rows
Calculation: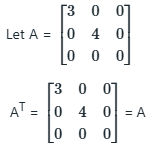
A is a symmetric matrix
|
113 videos|175 docs
|
FAQs on Definition of a Matrix - Matrices and Determinants, Business Mathematics & Statistics - Business Mathematics and Statistics - B Com
| 1. What is a matrix? |  |
| 2. What is the difference between a row matrix and a column matrix? |  |
| 3. How are matrices used in business mathematics and statistics? |  |
| 4. What is the determinant of a matrix? |  |
| 5. How can matrices and determinants be applied in real-world business scenarios? |  |






















