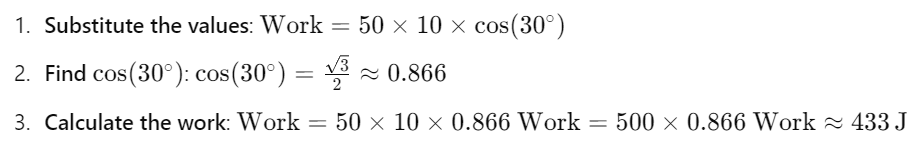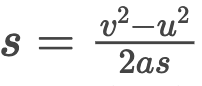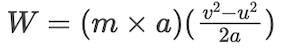Work and Energy Class 9 Notes Science Chapter 10
| Table of contents |

|
| Work, Power, and Energy |

|
| What is Work? |

|
| What is Energy? |

|
| Law of Conservation of Energy |

|
| Rate of Doing Work or Power |

|
Work, Power, and Energy
In earlier chapters, we learned about motion, its causes, and gravitation. Now, we explore another key idea—work, and its close partners, energy and power.
- Energy is what keeps both living beings and machines going. We use it for everything—from running, playing, and thinking to operating engines and machines. Animals, too, need energy to survive, move, and help in tasks like carrying loads or ploughing fields.
- Whether it comes from food or fuels like petrol and diesel, energy is what makes work possible. In this chapter, we’ll see how work and energy are connected and how they shape the world around us.
What is Work?
In our daily lives, we often refer to "work" as activities that require physical or mental effort. However, the scientific definition of work might differ from our usual understanding.
For instance, if you push a rock and it doesn’t move, even if you feel tired, scientifically, no work has been done. 
Scientific Conception of Work
In scientific terms, work is defined as applying force to an object that causes it to move. Work done is calculated by multiplying the force applied by the distance the object moves in the direction of that force. Here are a few examples to clarify this concept:
- Pushing a pebble: When you push a pebble and it moves, you apply force, and the pebble is displaced. Work is done here.
- Pulling a trolley: If a girl pulls a trolley and it moves, the force she applies and the trolley's movement mean work is done.
- Lifting a book: When you lift a book, your force moves it upwards, so work is accomplished.
For work to occur, two key conditions must be satisfied:
- There must be an application of force on the object.
- The object must be displaced in the direction of the force.
It's important to note that if there is no movement of the object, then the work done is zero. Additionally, an object capable of doing work is said to have energy.
Mathematically, the work done is calculated as: 
Work done = force x displacement
where:
- F is the constant force applied.
- S is the displacement in the direction of the force.
The SI unit of work is the joule (J or Nm). Work has magnitude but no direction.
In summary, work occurs when a force makes an object move in that direction, and it is measured by the product of force and distance moved.
Work is a fundamental concept linked to energy, which exists in different forms such as kinetic energy and potential energy. Understanding work is essential for learning about energy conservation and transformation.
Work Done By A Constant Force
Work done on an object is defined as the amount of force multiplied by the distance the object moves in the direction of the applied force.
- Work has only magnitude and no direction.
- The unit of work is joule:
1 Joule (J) = 1 Newton × 1 metre (N·m) - Here, the unit of work is Newton metre (Nm) or joule (J).
- Thus, 1 J is the amount of work done on an object when a force of 1 N displaces it by 1 m along the direction of the force.
Work done on an object by a force would be zero if the displacement of the object is zero.
Example 1
A force of 10 Newtons is applied to an object, causing it to be displaced by 5 meters. What is the work done on the object?
We can use the formula: W = F x S
Force (F) = 10 Newtons
Displacement (S) = 5 meters
Putting these values into the equation, we have:
W = (10 N) x (5 m) = 50 JoulesTherefore, the work done on the object is 50 Joules.
Example 2
A porter lifts a load of 15 kg from the ground and puts it on his head 1.5 m above the ground. Calculate the work done by him on the luggage.
- Mass of luggage, m = 15 kg
- Displacement, s = 1.5 m
- Work done, W = F × s = mg × s = 15 kg × 10 m/s² × 1.5 m = 225 kg m/s² m = 225 Nm = 225 J
Work done is 225 J.
Force at an Angle
When a force is applied at an angle to the direction of displacement, only a part of the force causes motion. The formula to calculate work in such cases is: Work = Force × Distance × cos(θ).
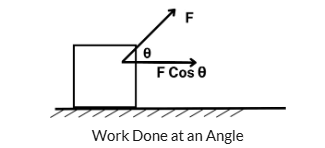
Where:
- Force is the magnitude of the constant force applied.
- Distance is the displacement of the object in the direction of the force.
- θ is the angle between the force and the displacement.
If the force and displacement are in the same direction (θ = 0), the formula simplifies to: Work = Force × Distance. This means that work done by a constant force is equal to the product of the force applied and the distance over which the force acts.
Example 3
A box is pushed with a force of 50 N at an angle of 30° to the horizontal. If the box moves 10 m, calculate the work done.
- Force (F) = 50 N
- Angle (θ) = 30°
- Distance (d) = 10 m
Formula: Work = F × d × cos(θ)
Step-by-step solution:
Answer: The work done is approximately 433 J (Joules).
Positive, Negative & Zero Work Done
- Positive Work: Work is considered positive if the displacement of the object is along the direction of the force applied.
Example: Work done by a man is taken as positive when he moves from the ground floor to the second floor of his house. - Negative Work: Work is taken as negative if the displacement of the object is in the direction opposite to the force applied.
Example: Work done by the man is negative when he descends from the second floor of the house to the ground floor.
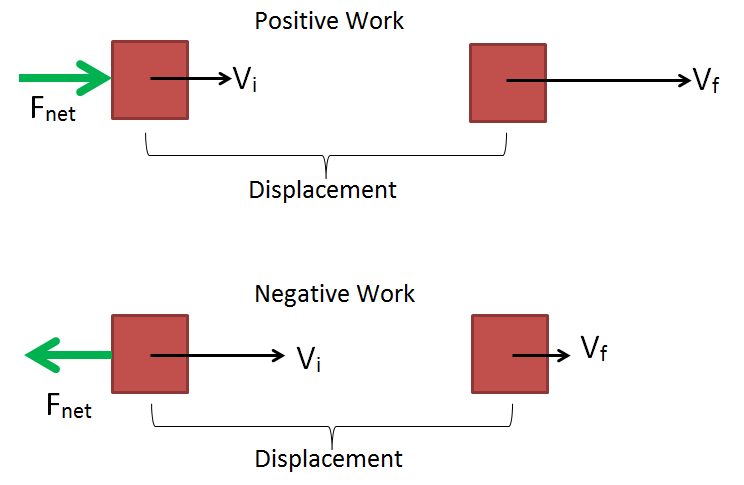 Positive and Negative Work Done
Positive and Negative Work Done
- Zero Work Done: If the displacement of an object is in a direction perpendicular to the application of force, work done is zero despite the fact that force is acting and there is some displacement too.
Example: Imagine pushing a lawn roller forward. While gravity pulls it downward, the roller moves horizontally. Since gravity acts perpendicular to the roller's movement, it does no work. This is an example of zero work, where a force doesn't contribute to the displacement.
The gravitational potential energy of an object of mass m raised through a height, h, from the Earth's surface is given by mgh.
What is Energy?
An object that can do work is said to have energy. Therefore, the energy of an object is its ability to perform work. When an object does work, it loses energy, while the object that receives the work gains energy. This means energy is transferred from one object to another. The unit of energy is the same as that of work, which is the joule (J). One joule is the energy needed to do one joule of work. A larger unit, the kilojoule (kJ), is also used, where 1 kJ equals 1000 J.
- An object with energy can apply force on another object.
- The energy of an object is measured by its ability to do work, indicating that any object with energy can perform work.
 Energy Transformation
Energy Transformation
Forms of Energy
Energy exists in various forms in nature, including:
- Mechanical energy
- Heat energy
- Electrical energy
- Light energy
- Chemical energy
- Nuclear energy
Mechanical energy can be divided into two types:
- Kinetic energy
- Potential energy
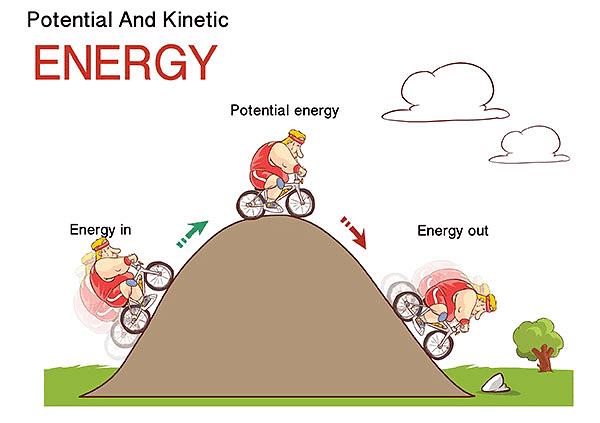 Potential and Kinetic Energy
Potential and Kinetic Energy
Kinetic Energy
The kinetic energy of an object is the energy possessed by it by virtue of its state of motion. A speeding vehicle, a rolling stone, a flying aircraft, flowing water, blowing wind, and a running athlete possess kinetic energy.
For an object of mass m and having a speed v, the kinetic energy is given by:
F = ma
Also, W=Fs
From the second equation of motion, we know that
v2 - u2 = 2as
Rearranging the equation, we get
Substituting equation for work done by a moving body,
Taking initial velocity as zero, we get
where:
- Ek is the kinetic energy.
- m is the mass of the object.
- v is the velocity of the object
Note : When two identical bodies are in motion, the body with a higher velocity has more KE.
Potential Energy
An object gains energy when it is lifted to a higher position because work is done against the force of gravity. This energy is known as gravitational potential energy. Gravitational potential energy is defined as the work done to raise an object from the ground to a certain height against gravity.
Let's consider an object with a mass m being lifted to a height h above the ground.
The minimum force required to lift the object is equal to its weight, which is mg(where g is the acceleration due to gravity).
The work done on the object to lift it against gravity is given by the formula:
Work Done (W) = Force × Displacement
W = mg × h = mgh
The energy gained by the object is equal to the work done on it, which is mgh units.
This energy is the potential energy (Ep) of the object.
Ep = mgh
Note: It's important to note that the work done by gravity depends only on the difference in vertical heights between the initial and final positions of the object, not on the path taken to move the object. For example, if a block is raised from position A to position B by taking two different paths, as long as the vertical height AB is the same (h), the work done on the object is still mgh.
Potential Energy of an Object at Height
Let's consider an object with a mass m being lifted to a height h above the ground.
The minimum force required to lift the object is equal to its weight, which is mg (where g is the acceleration due to gravity).
The work done on the object to lift it against gravity is given by the formula:
Work Done (W) = Force × Displacement
W = mg × h = mgh
Since work done on the object is equal to mgh, an energy equal to mgh units is gained by the object. This is the potential energy (Ep) of the object.
Potential Energy (Ep) = mgh
Note: The work done by gravity depends only on the difference in vertical heights between the initial and final positions of the object, not on the path taken to move the object. For example, if a block is raised from position A to position B by taking two different paths, as long as the vertical height AB is the same (h), the work done on the object is still mgh.
Example 5
Find the energy possessed by an object of mass 10 kg when it is at a height of 6 m above the ground.
Given g = 9.8 m/s².
- Mass (m) = 10 kg
- Height (h) = 6 m
- Acceleration due to gravity (g) = 9.8 m/s²
Using the formula for potential energy: Ep = mgh
Substituting the values, we have:
Potential Energy = 10 × 9.8 × 6 = 588 J
Therefore, the potential energy of the object is 588 Joules.
Example 6
An object of mass 12 kg is at a certain height above the ground. If the potential energy of the object is 480 J, find the height at which the object is with respect to the ground. Given g = 10 m/s².
Mass of the object, m = 12 kg, potential energy, E = 480 J.
Using the formula E = mgh:
480 J = 12 × 10 × h
Solving for h:
h = 480 J / 120 kg m/s² = 4 m
The object is at a height of 4 m.
Law of Conservation of Energy
According to the law of conservation (transformation) of energy, we can neither create nor destroy energy. Energy can only change from one form to another; it cannot be created or destroyed. The total energy before and after the change remains constant. The total mechanical energy of an object is the sum of its kinetic energy and potential energy.
- For an object falling freely, the potential energy decreases as it falls and transforms into kinetic energy. This process does not break the law of conservation of energy; instead, it demonstrates it, since the total mechanical energy remains unchanged during the fall.
- As the object continues to fall, its potential energy decreases while its kinetic energy increases. If v is the object's velocity at a given moment, the kinetic energy is 1/2 mv². Just before hitting the ground, h = 0, and v is at its maximum. Therefore, the kinetic energy is highest and the potential energy is lowest just before the object reaches the ground. However, the sum of potential energy and kinetic energy remains the same at all points, illustrating the law of conservation of energy.
Potential Energy + Kinetic Energy = Constant
or
mgh + 1/2 mv² = constant
The law of conservation of energy applies in all scenarios and for all types of transformations.
The diagram below shows a pendulum, which consists of a mass (m) connected to a fixed pivot point via a string of length (L).
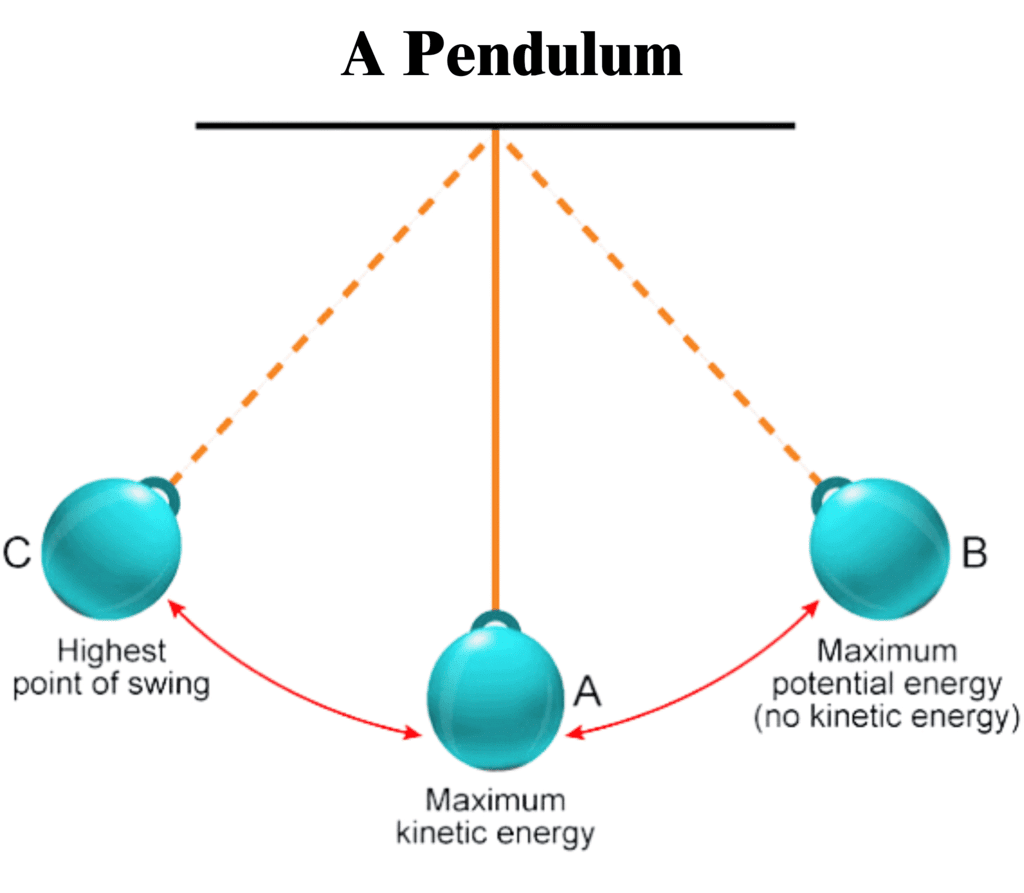
Positions of the Pendulum
- At the highest point (A): Here, the pendulum is briefly at rest, and all its energy is potential energy (PE). The height (h) of the mass above the lowest point determines how much potential energy it has. The potential energy can be calculated using the formula: PE = m · g · h, where g is the acceleration due to gravity.
- At the lowest point (B): As the pendulum swings down, its potential energy is changed into kinetic energy (KE). At this point, its height (h) is zero, meaning it has no potential energy. Here, all its energy is kinetic energy, and the pendulum is moving at its highest speed. The kinetic energy can be calculated using the formula: KE = ½ m · v², where v is the velocity of the mass.
- At the highest point on the other side (C): As the pendulum swings upwards, its kinetic energy is transformed back into potential energy.
The total mechanical energy of the pendulum, which is the sum of kinetic energy and potential energy, stays the same throughout its motion. This shows the law of conservation of energy, which states that energy cannot be created or destroyed; it can only be changed from one form to another.
In essence, the energy changes in a pendulum illustrate that the total mechanical energy remains constant, confirming that the total energy before and after the change is unchanged.
Rate of Doing Work or Power
The rate at which work is done or energy is transferred is known as Power. Power indicates how quickly or slowly work is performed. The formula for calculating power is:
Power = Work done / Time taken
- The SI unit of power is a watt (W). One watt is defined as the power of an agent that does work at the rate of 1 joule per second (1 W = 1 J/s).
- We use larger units for energy transfer, such as kilowatts (kW): 1 kilowatt = 1 kW = 1000 watts.
- Other common units of power include:
- 1 megawatt (MW) = 106 watts
- 1 horsepower (hp) = 746 watts
Average Power
Understanding average power is important because it helps us see how quickly work is done over time, even if that speed changes. You can calculate average power by dividing the total energy used by the total time taken. This results in a single number that shows the overall power, regardless of variations in the work rate.
- Average Power = Total energy consumed (or total work done) / Total time
- The power of a person can change over time, meaning they might work at different speeds during various intervals.
According to the law of conservation of energy, energy can only change forms; it cannot be created or destroyed. The total energy before and after any change always remains constant. Energy exists in various forms in nature, such as kinetic energy, potential energy, heat energy, and chemical energy. The total of kinetic and potential energies in an object is referred to as its mechanical energy.
|
84 videos|541 docs|60 tests
|
FAQs on Work and Energy Class 9 Notes Science Chapter 10
| 1. What is work in physics, and how is it calculated? |  |
| 2. What is the relationship between work and energy? |  |
| 3. What is power, and how is it different from work? |  |
| 4. What is the Law of Conservation of Energy? |  |
| 5. How can we apply the concepts of work, power, and energy in daily life? |  |