Class 10 Exam > Class 10 Notes > Mathematics (Maths) Class 10 > Unit Test: Real Numbers
Unit Test: Real Numbers | Mathematics (Maths) Class 10 PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each.
Q1: Which of the following numbers is irrational? (1 Mark)
(a) √25
(b) 3.14
(c) π
(d) -7
Q2: What is the value of (5² + 12²)? (1 Mark)
(a) 169
(b) 144
(c) 25
(d) 169√2
Q3: Which one is not a prime number? (1 Mark)
(a) 1
(b) 2
(c) 3
(d) 5
Q4: State whether "√16" is a rational number or not. (1 Mark)
Q5:What is the prime factorization of 96? (1 Mark)
Q6: Prove that the square of any positive integer of the form (5k + 1) is one more than a multiple of 8, where "k" is an integer. (2 Marks)
Q7: Prove that √2 is irrational. (2 Marks)
Q8: Find the LCM (Least Common Multiple) of 15 and 20. (2 Marks)
Q9: Sonia takes 18 minutes to complete one round of a circular track, while Ravi takes 12 minutes for the same. If they start together from the same point, after how many minutes will they meet again at the starting point? (3 Marks)
Q10: Find the HCF (Highest Common Factor) of 72 and 96 using the prime factorization method. (3 Marks)
Q11: Check whether 6n can end with the digit 0 for any natural number n(3 Marks)
Q12: Given that p is a rational number and q is an irrational number, prove that their sum (p + q) is an irrational number. (5 Marks)
Q13: Prove that 5√3 - 3√75 is an irrational number. (5 Marks)
You can find the solutions of this Unit Test here: Unit Test (Solutions): Real Numbers
The document Unit Test: Real Numbers | Mathematics (Maths) Class 10 is a part of the Class 10 Course Mathematics (Maths) Class 10.
All you need of Class 10 at this link: Class 10
|
127 videos|680 docs|84 tests
|
FAQs on Unit Test: Real Numbers - Mathematics (Maths) Class 10
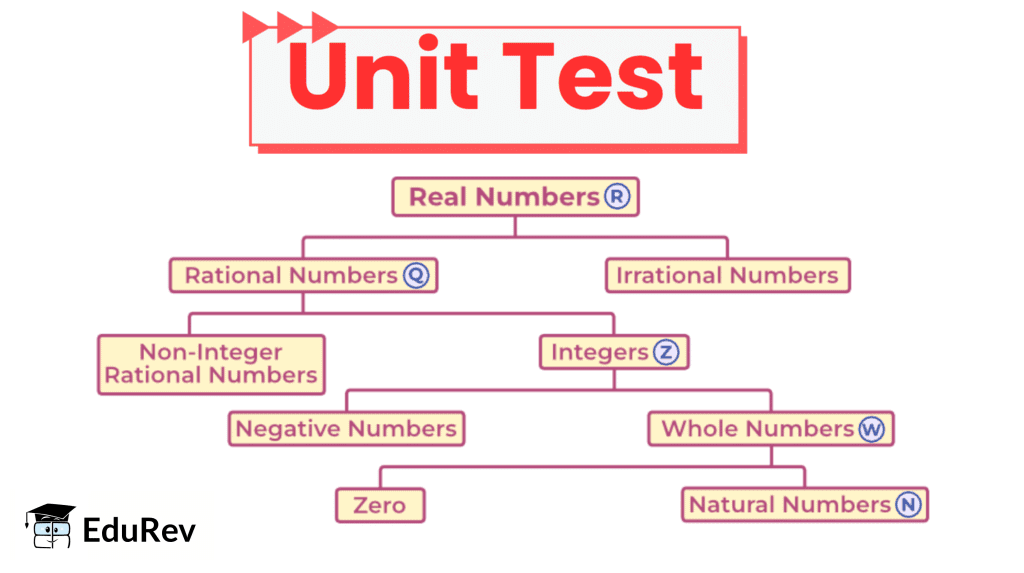
| 1. What are real numbers and how are they classified? |  |
Ans. Real numbers are the set of numbers that include all the rational and irrational numbers. They can be classified into several categories: natural numbers (1, 2, 3,...), whole numbers (0, 1, 2, 3,...), integers (...,-2, -1, 0, 1, 2,...), rational numbers (numbers that can be expressed as a fraction of two integers, such as 1/2, -3/4), and irrational numbers (numbers that cannot be expressed as a simple fraction, such as √2, π).
| 2. How do you perform operations with real numbers? | |
Ans. Operations with real numbers include addition, subtraction, multiplication, and division. To perform these operations, you need to follow the standard arithmetic rules. For instance, when adding or subtracting real numbers, you align them based on their decimal points. For multiplication, you multiply the numbers directly, and for division, you divide the numerator by the denominator. When dealing with irrational numbers, it is important to leave them in their radical form unless specified.
| 3. What is the difference between rational and irrational numbers? | |
Ans. Rational numbers are numbers that can be expressed as a fraction where both the numerator and denominator are integers, and the denominator is not zero (e.g., 1/3, -2). Irrational numbers, on the other hand, cannot be expressed as a simple fraction. They have non-repeating, non-terminating decimal expansions (e.g., √3, π). The key difference is that rational numbers can be written as a fraction, while irrational numbers cannot.
| 4. How can real numbers be represented on a number line? | |
Ans. Real numbers can be represented on a number line by marking specific points that correspond to each number. The number line is a straight horizontal line where each point represents a real number. Positive numbers are located to the right of zero, while negative numbers are to the left. Rational numbers can be plotted as exact points, while irrational numbers are also represented, though they may not correspond to exact locations. The distance between points reflects the value of the numbers.
| 5. What are some common properties of real numbers? | |
Ans. Real numbers exhibit several important properties, including the commutative property (a + b = b + a and ab = ba), associative property ((a + b) + c = a + (b + c) and (ab)c = a(bc)), distributive property (a(b + c) = ab + ac), identity property (a + 0 = a and a × 1 = a), and inverse property (a + (-a) = 0 and a × (1/a) = 1 for a ≠ 0). These properties are essential for simplifying expressions and solving equations involving real numbers.
About this Document
8.4K Views
4.98/5
Rating
Sep 04, 2025
Last updated
Document Description: Unit Test: Real Numbers for Class 10 2025 is part of Mathematics (Maths) Class 10 preparation.
The notes and questions for Unit Test: Real Numbers have been prepared according to the Class 10 exam syllabus. Information about Unit Test: Real Numbers covers topics
like and Unit Test: Real Numbers Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Unit Test: Real Numbers.
Introduction of Unit Test: Real Numbers in English is available as part of our Mathematics (Maths) Class 10
for Class 10 & Unit Test: Real Numbers in Hindi for Mathematics (Maths) Class 10 course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Unit Test: Real Numbers | Mathematics (Maths) Class 10
Description
Full syllabus notes, lecture & questions for Unit Test: Real Numbers | Mathematics (Maths) Class 10 - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 10 | Best notes, free PDF download
Information about Unit Test: Real Numbers
In this doc you can find the meaning of Unit Test: Real Numbers defined & explained in the simplest way possible. Besides explaining types of
Unit Test: Real Numbers theory, EduRev gives you an ample number of questions to practice Unit Test: Real Numbers tests, examples and also practice Class 10
tests
Related Searches
Unit Test: Real Numbers | Mathematics (Maths) Class 10
,Important questions
,ppt
,mock tests for examination
,study material
,Unit Test: Real Numbers | Mathematics (Maths) Class 10
,Exam
,Summary
,Previous Year Questions with Solutions
,MCQs
,Unit Test: Real Numbers | Mathematics (Maths) Class 10
,shortcuts and tricks
,Free
,Viva Questions
,practice quizzes
,past year papers
,Extra Questions
,Semester Notes
,video lectures
,Objective type Questions
,Sample Paper
;
Additional Information about Unit Test: Real Numbers for Class 10 Preparation
Unit Test: Real Numbers Free PDF Download
The Unit Test: Real Numbers is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Unit Test: Real Numbers now and kickstart your journey towards success in the Class 10 exam.
Importance of Unit Test: Real Numbers
The importance of Unit Test: Real Numbers cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Unit Test: Real Numbers Notes
Unit Test: Real Numbers Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Unit Test: Real Numbers.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Unit Test: Real Numbers Notes on EduRev are your ultimate resource for success.
Unit Test: Real Numbers Class 10 Questions
The "Unit Test: Real Numbers Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Unit Test: Real Numbers on the App
Students of Class 10 can study Unit Test: Real Numbers alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Unit Test: Real Numbers,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Unit Test: Real Numbers is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup