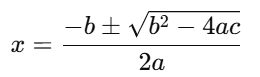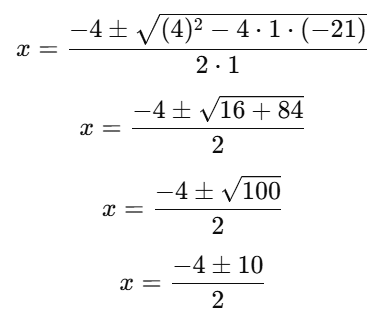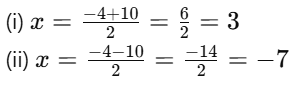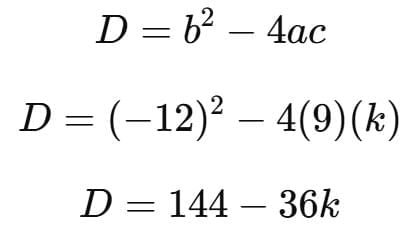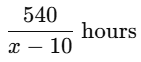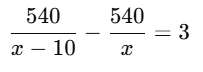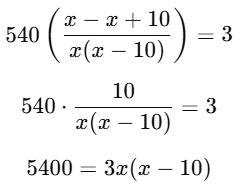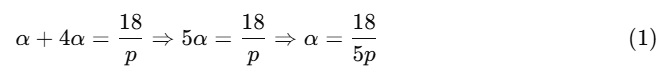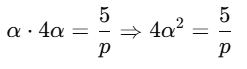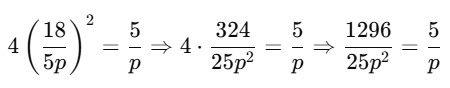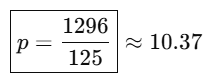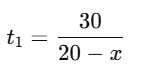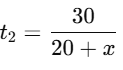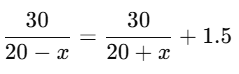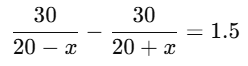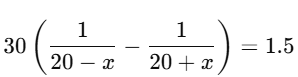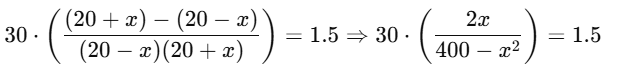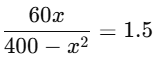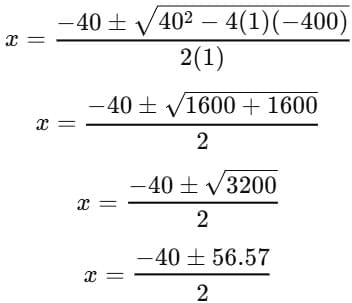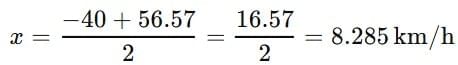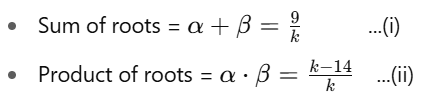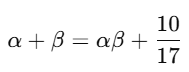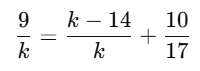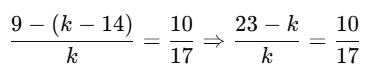Sure Shot Questions for Board Exams: Quadratic Equations | Mathematics (Maths) Class 10 PDF Download

Q1. The roots of the equation x² + 4x – 21 = 0 are:
(a) 3, –7
(b) –3, 7
(c) 2, –6
(d) –2, 6
Ans: (a)
To find the roots of the quadratic equation x2 + 4x − 21 = 0, we can use the quadratic formula:
For the equation x2 + 4x − 21 = 0:
- a=1
- b=4
- c=−21
Substitute these values into the formula:
Now, calculate the two roots:
So, the roots of the equation are 3 and –7.
Q2. If the roots of the quadratic equation 9x² − 12x + k = 0 are real and equal, then the value of k is:
(a) 4 /3
(b) 16
(c) 4
(d) 9/4
Ans: (c)
Given that the roots of the quadratic equation
9x2 −12x + k = 0 are real and equal,
Comparing with the standard form ax2 + bx + c = 0:
- a=9,
- b=−12,
- c=k
For real and equal roots, We use the condition:
b2 − 4ac = 0
Substitute values:For equal roots, 144 - 36k = 0
144 = 36k
k = 144 / 36 = 4So , k = 4
Q3. A train covers a distance of 540 km at a uniform speed. If the speed had been 10 km/h less, it would have taken 3 hours more to cover the same distance. Find the original speed of the train.
Sol: Let the original speed of the train be x km/h.
Then, time taken to cover the journey of 540 km = 540/x hours
Time taken to cover the same distance at speed (x−10) km/h =
Now, according to the question:
Take LCM and simplify:
3x(x−10)=5400
⇒x(x−10)=1800
x2−10x−1800=0
(x - 48)(x+38) = 0
x=−38 (not possible) or x=48
∴ The original speed of the train is 48 km/h.
Q4. The least positive value of k for which the quadratic equation 3x² + kx + 6 = 0 has rational roots is:
(a) ±3
(b)9
(c) ±√3
(d) 3√2
Ans: (b)
Step 1:Middle-Term Splitting
In the quadratic equation ax² + bx + c = 0, we use middle-term splitting to break the middle term (bx) into two terms that help us factor the equation easily.
We need to split the middle term (kx) into two numbers such that:
Their sum is equal to k.
Their product is equal to a × c (in this case, 3 × 6 = 18).
Step 2: Find the Factor Pairs of 18
We need to find two numbers that multiply to give 18 and add up to k.
Possible factor pairs of 18 are:
9 × 2 = 18, and 9 + 2 = 11 (this would give k = 11),
6 × 3 = 18, and 6 + 3 = 9 (this would give k = 9),
-9 × -2 = 18, and -9 + (-2) = -11 (this would give k = -11),
-6 × -3 = 18, and -6 + (-3) = -9 (this would give k = -9).
Step 3: Check for the Least Positive k
From the possible values of k:
k = 11
k = 9 (This is the least positive value)
Q5. The hypotenuse (in cm) of a right-angled triangle is 6 cm more than twice the shortest side. If the third side is 6 cm less than thrice the shortest side, find the dimensions of the triangle.
Sol:
Step 1: Define the Variables
Let the shortest side of the right-angled triangle be x cm.
The hypotenuse is 6 cm more than twice the shortest side, so:
Hypotenuse = 2x + 6 cm.
The third side (the other leg) is 6 cm less than thrice the shortest side, so:
Third side = 3x - 6 cm.
Step 2: Apply the Pythagorean Theorem
In a right-angled triangle, the Pythagorean theorem states that:
(Hypotenuse)² = (Shortest side)² + (Third side)²
Now, substitute the expressions for the hypotenuse, shortest side, and third side:
(2x + 6)² = x² + (3x - 6)²
Step 3: Expand the Equation
First, expand both sides:
Left-hand side:
(2x + 6)² = 4x² + 24x + 36
Right-hand side:
x² + (3x - 6)² = x² + (9x² - 36x + 36) = 10x² - 36x + 36
Step 4: Set up the Equation
Now, equate both sides:
4x² + 24x + 36 = 10x² - 36x + 36
Step 5: Simplify the Equation
Move all terms to one side:
4x² + 24x + 36 - 10x² + 36x - 36 = 0
Simplify:
-6x² + 60x = 0
Factor out common terms:
-6x(x - 10) = 0
Step 6: Solve for x
Now, solve for x:
x = 0 or x = 10
Since the side length cannot be zero, we take x = 10 cm.
Q6. Find the value of p, for which one root of the quadratic equation px2 − 18x + 5 = 0 is 4 times the other.
Sol: Let one root be α,
Then the other root = 4α
Step 1: Use the sum of roots
Step 2: Use the product of roots
Substitute value of α from (1):
Cross-multiply:
1296p = 125p2 ⇒ 125p2 − 1296p = 0 ⇒ p(125p−1296)=0
So, p=0 or p = 1296/125
Since 𝑝 ≠ 0, we take:
Q7. A motorboat whose speed is 20 km/h in still water takes 1.5 hours more to go 30 km upstream than to return downstream to the same spot. Find the speed of the stream.
Sol: Speed of boat in still water = 20 km/h
Distance = 30 km
Let the speed of the stream be x km/h
Time for upstream:
Speed = 20−x
Time for downstream:
Speed = 20 + x
According to the question:
Simplify the equation:
Take LHS:
Multiply both sides by 400 − x2:
60x = 1.5(400 − x2) ⇒ 60x = 600 − 1.5x2
Multiply both sides by 2 to remove the decimal:
120x = 1200 − 3x2 ⇒ 3x2 + 120x − 1200 = 0
Divide by 3:
x2 + 40x − 400 = 0
Q8. If the sum of the roots of the quadratic equation ky2 - 9y + (k - 14) = 0 is 10/17 more than the product of the roots, then find the value of k.
Sol: Given quadratic equation:
ky2−9y+(k−14)=0
Let the roots be α and β.
Step 1: Use sum and product of rootsStep 2: Use the condition from the question
According to the question:
Substitute (i) and (ii):
Step 3: Simplify the equation
Cross-multiply:
17(23 − k) = 10k
⇒ 391 − 17k = 10k
⇒ 391 = 27k
⇒ k = 391/27
⇒ k = 14.48
|
127 videos|655 docs|84 tests
|
FAQs on Sure Shot Questions for Board Exams: Quadratic Equations - Mathematics (Maths) Class 10
| 1. What is the standard form of a quadratic equation? |  |
| 2. How can you solve a quadratic equation using the quadratic formula? |  |
| 3. What is the discriminant, and how does it affect the roots of a quadratic equation? |  |
| 4. Can you explain what completing the square means in relation to quadratic equations? |  |
| 5. What are the graphical representations of quadratic equations? |  |