Sampling Theorem | Network Theory (Electric Circuits) - Electrical Engineering (EE) PDF Download

The sampling theorem is a foundational principle in network theory and signal processing, enabling the accurate representation and reconstruction of continuous-time signals in discrete-time form. This theorem is critical for systems involving digital networks, communication, and control, where signals must be sampled, processed, and analyzed efficiently.

Statement of the Sampling Theorem

The sampling theorem states that a continuous-time signal $x\left(t\right)x(t)$, bandlimited to a maximum frequency $WW$ Hz (i.e., its Fourier transform $\mathrm{<br>}X(f)\; =\; 0$X(f)=0 for $\mathrm{<br>}|f|\; >\; W$∣f∣>W), can be perfectly reconstructed from its discrete-time samples $x\left(nTs\right)x(nT\_s)$ provided the sampling frequency 
$Fs=1/TsF\_s\; =\; 1/T\_s$ satisfies:

$F\_s\; >\; 2W$Fs>2W

Here, Ts is the sampling period, and $\mathrm{ }2W$2W is the Nyquist rate. This condition ensures that the discrete samples capture all information in 
x(t), allowing exact recovery of the original signal.

Mathematical Foundation and Proof

Sampling involves multiplying the continuous-time signal $x\left(t\right)x(t)$x(t) by an impulse train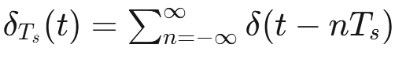 

where $\delta \left(t\right)\backslash delta(t)$ is the Dirac delta function. The resulting sampled signal is:

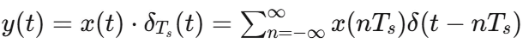
The impulse train $\delta Ts\left(t\right)\backslash delta\_\{T\_s\}(t)$ has a Fourier series representation:

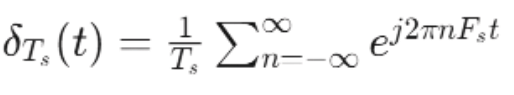
Substituting into $y\left(t\right)y(t)$:

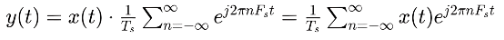
This reveals that $Y\left(f\right)Y(f)$ consists of replicas of $X\left(f\right)X(f)$ shifted by multiples of $FsF\_s$ and scaled by $1/Ts1/T\_s$. For $\mathrm{<br>}x(t)$x(t) to be recoverable, these replicas must not overlap, requiring $Fs>2WF\_s\; >\; 2W$. An ideal low-pass filter with cutoff between $WW$ and $Fs-WF\_s\; -\; W$ can then extract $X\left(f\right)X(f)$ from $Y\left(f\right)Y(f)$,enabling reconstruction.

Impulse Train and Sampling Process

The impulse train $\delta Ts\left(t\right)\backslash delta\_\{T\_s\}(t)$ acts as a sampling comb, selecting instantaneous values of $\mathrm{<br>}x(t)$x(t) at intervals $TsT\_s$. Its periodicity in the time domain translates to a discrete spectrum in the frequency domain, with energy concentrated at multiples of $FsF\_s$. This periodic sampling modulates $\mathrm{<br>}\mathrm{<br>}x(t)$x(t), creating the replicated spectrum $\mathrm{<br>}Y(f)$Y(f), which underscores the importance of choosing an appropriate $FsF\_s$.

Nyquist Sampling Theorem

The Nyquist sampling theorem defines the minimum sampling rate as $Fs\ge 2WF\_s\; \backslash geq\; 2W$ to prevent spectral overlap. This threshold, known as the Nyquist criterion, ensures that the sampled signal retains all frequency components of $x\left(t\right)x(t)$ without ambiguity.

Shannon Sampling Theorem

The Shannon sampling theorem provides the reconstruction framework, stating that a bandlimited signal is fully determined by samples taken at intervals $Ts\le 1/\left(2W\right)T\_s\; \backslash leq\; 1/(2W)$. The signal can be reconstructed using the interpolation formula:

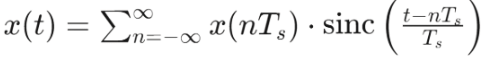
where $sincsinc(u)=\sin (\pi u\left)/\right(\pi u)\backslash text\{sinc\}(u)\; =\; \backslash sin(\backslash pi\; u)/(\backslash pi\; u)$ is the ideal interpolation kernel. This sinc function arises from the rectangular low-pass filter in the frequency domain used for reconstruction.

Reconstruction and Interpolation

Reconstruction relies on interpolating the discrete samples $x\left(nTs\right)x(nT\_s)$ back to a continuous signal. The sinc function, being the impulse response of an ideal low-pass filter, ensures perfect recovery by weighting each sample according to its temporal proximity to $tt$. In practice, finite-length interpolation (e.g., using windowed sinc functions) approximates this ideal process due to computational constraints.

Frequency Domain Implications

In the frequency domain, sampling introduces periodicity in $Y\left(f\right)Y(f)$. If $Fs<2W$, the shifted replicas overlap, causing aliasing (discussed below). Conversely, oversampling ($\mathrm{<br>}F\_s\; \backslash gg\; 2W$Fs≫2W) widens the guard band between replicas, simplifying filter design but increasing data rates. This trade-off is a key consideration in network system design.

Applications in Network Theory

The sampling theorem underpins several critical applications:

• Digital Communication: Sampling converts analog signals into discrete sequences for modulation and transmission over digital channels.
• Networked Control Systems: Discrete-time sampling enables digital controllers to process continuous sensor data.
• Signal Analysis: Fourier and spectral analysis in networks rely on sampled data to characterize system behavior.

Aliasing Effect

Aliasing occurs when Fs<2W, causing overlap of spectral replicas. High-frequency components of $\mathrm{<br>}$x(t) are misinterpreted as lower frequencies in the reconstructed signal, resulting in irreversible distortion. Anti-aliasing filters, applied prior to sampling, limit the signal bandwidth to $\mathrm{<br>}W$W, ensuring compliance with the Nyquist criterion.

Practical Considerations

• Non-Ideal Filters: Real-world low-pass filters have roll-off rather than sharp cutoffs, necessitating $\mathrm{<br>}F\_s$Fs slightly above $\mathrm{<br>}2W$2W for margin.
• Signal Bandwidth: Accurately determining $\mathrm{<br>}W$W is crucial; if underestimated, aliasing persists despite meeting $F\_s\; >\; 2W$Fs>2W.
•  Quantization Effects: Sampling is often paired with quantization in digital systems, introducing noise not addressed by the theorem.

Conclusion

These practical considerations highlight the gap between the sampling theorem’s ideal conditions and real-world implementation. Non-ideal filters necessitate a safety margin in $FsF\_s$Fs, accurate bandwidth estimation prevents aliasing, and quantization introduces noise not addressed by the theorem. Addressing these factors ensures that the theorem’s principles are effectively applied in network theory, delivering robust and reliable system performance.