Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Revision Notes: Ratio and Proportion
Revision Notes: Ratio and Proportion | Mathematics Class 10 ICSE PDF Download
Important Concepts-Ratio
- The ratio between x and y is the fraction (x/y) and written as x : y, where, y ≠ 0
Here, the first quantity x is known as Antecedent and second quantity y is known as Consequent. - The ratio (x/y) has no unit.
- Ratio is taken only between positive quantities.
- Ratio exists only between two quantities of the same kind.
- The value of a ratio remains unchanged, if both the antecedent (Nr) and the consequent (Dr) are multiplied or divided by the same quantity.
- The ratio is in its lowest terms if the H.C.F of its both the terms is unity, 1.
- Ratio a : b is not equal to b:a, unless a = b
- If a quantity increases or decreases in the ratio a : b, the new resulting quantity is equal to (b/a) times of a the original quantity.
- Compounded Ratio is the ratio obtained by multiplying two or more ratios together
Let a : b and x : y be the two ratios then their compounded ratio be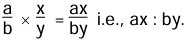
Compounded ratio of a:b, c:d and e:f is ace : bdf - Duplicate ratio is the compound ratio of two equal ratios.
Duplicate ratio of x : y is x2 : y2. - Triplicate ratio is the compound ratio of three equal ratios.
Triplicate ratio of x : y is x3 : y3 . - Sub-duplicate ratio of x : y is
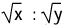 .
.
The sub-triplicate ratio of x: y is x1/3 : y1/3 . - The reciprocal ratio is the ratio between the reciprocals of two quantities.
The reciprocal ratio of x : y is (1/x) : (1/y) i.e., y : x.
Important Concepts-Proportion
- a : b : : c : d
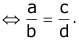
This is called cross product rule.
If four quantities a, b, c and d are such that the ratio a:b is equal to the ratio c:d then we say a, b, c and d are in proportion. We express it by writing a:b :: c:d. Here, a and d are called extreme terms while b and c are called the middle terms. Here, d is called the fourth proportional. - Three numbers a, b and c are said to be in continued proportion if a:b::b:c that is
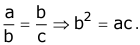
- If a, b and c are in continued proportion then b is called the mean proportional or geometric mean of a and c. Thus,
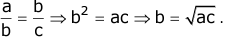
- If a, b, c, d, e, f, … are in continued proportion if and only if,
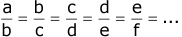
- If a, b and c are in continued proportion, then ‘a’ is called the first proportional.
- If a, b and c are in continued proportion, then ‘c’ is called the third proportional.
Some properties of Ratio and Proportion
- Invertendo: If a:b:c:d then b:a::d:c, that is

- Alternendo: If a:b:c:d then a:c::b:d, that is
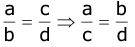
- Componendo: If a:b:c:d then that is (a + b):b: :(c + d):d, that is
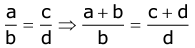
- Dividendo: If a:b:c:d then (a - b):b: :(c - d):d, that is
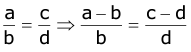
- Componendo and Dividendo: If a:b:c:d then
(a + b): (a - b):: (c + d): (c - d):, that is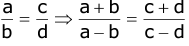
- Convertendo: If a:b:c:d then a:(a - b)::c:(c - d), that is
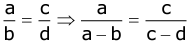
- For any two or more equal ratios, each ratio is equal to the ratio between sum of their antecedents and sum of their consequents.
Therefore, we have,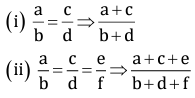
The document Revision Notes: Ratio and Proportion | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|276 docs|8 tests
|
FAQs on Revision Notes: Ratio and Proportion - Mathematics Class 10 ICSE
| 1. What is the definition of ratio and how is it expressed? |  |
Ans. A ratio is a relationship between two numbers that indicates how many times the first number contains the second. It is expressed in the form of a fraction, with the first number as the numerator and the second as the denominator. Ratios can also be written using a colon (:) notation, such as 3:2, which means for every 3 units of the first quantity, there are 2 units of the second quantity.
| 2. How do you simplify a ratio? |  |
Ans. To simplify a ratio, you divide both terms of the ratio by their greatest common divisor (GCD). For example, to simplify the ratio 8:12, you find the GCD of 8 and 12, which is 4. Then, divide both terms by 4, resulting in the simplified ratio of 2:3.
| 3. What is the difference between direct proportion and inverse proportion? |  |
Ans. Direct proportion means that as one quantity increases, the other quantity also increases, and they maintain a constant ratio. For instance, if you have a direct proportion between x and y, if x doubles, y also doubles. Inverse proportion, on the other hand, means that as one quantity increases, the other quantity decreases, maintaining a constant product. For example, if x increases and y is inversely proportional to x, then as x doubles, y will be halved.
| 4. How can ratios be used in real-life situations? |  |
Ans. Ratios are commonly used in various real-life situations, such as cooking, finance, and scaling models. For example, in cooking, a recipe may require a ratio of ingredients, such as 2 cups of flour to 1 cup of sugar. In finance, ratios like debt-to-equity can help assess a company’s financial health. Additionally, ratios are used in maps and models to represent scale, indicating how distances on the map relate to actual distances.
| 5. What are proportion problems and how can they be solved? |  |
Ans. Proportion problems involve finding an unknown quantity when two ratios are equivalent. To solve them, you can set up a proportion equation, such as a/b = c/d, where you cross-multiply to get ad = bc. Then, solve for the unknown variable. For example, if you need to find x in the proportion 3/4 = x/12, you cross-multiply to get 3 * 12 = 4 * x, leading to x = 9.
Related Searches















