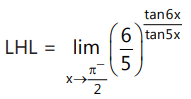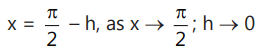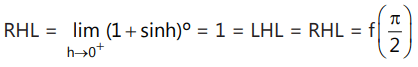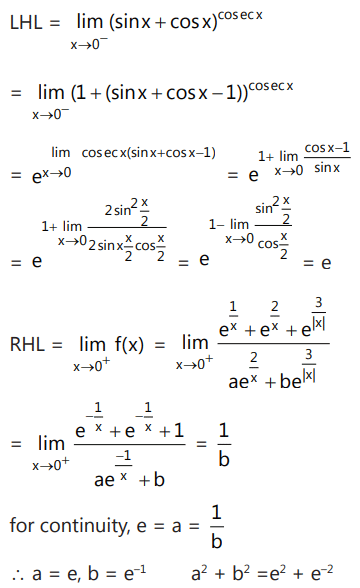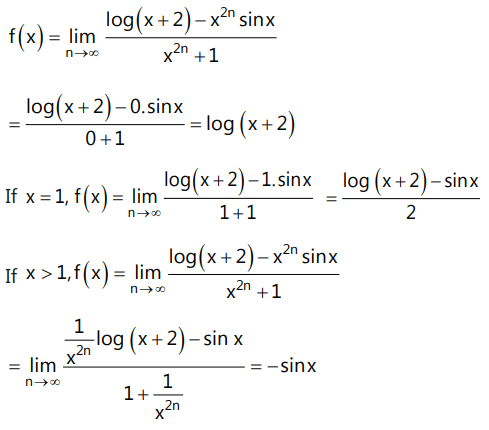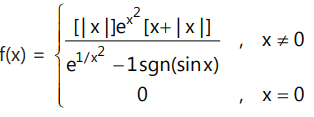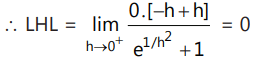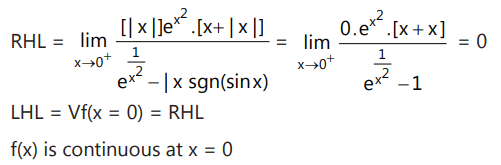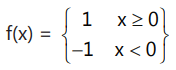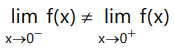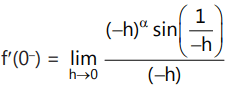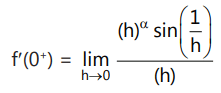Revision Notes: Continuity and Differentiability | Mathematics (Maths) for JEE Main & Advanced PDF Download

Important Formulas
1. Let f and g be two real functions with a common domain D, then.
(i)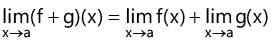
(ii)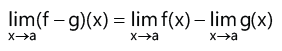
(iii)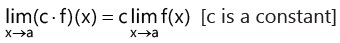
(iv)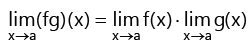
(v)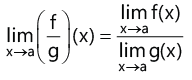
(vi)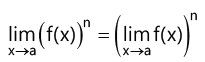
(vii)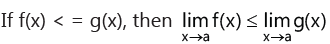
(viii)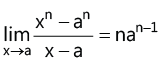
(ix)
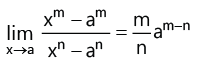
(x)
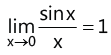
(xi)
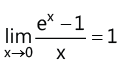
(xii)
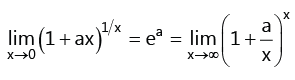
(xiii)
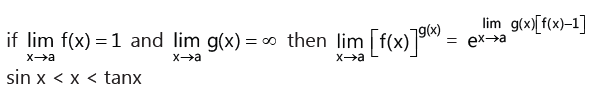
2. Expansions of Some Functions
(i)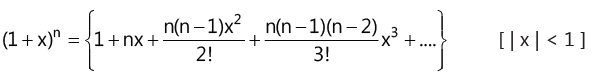
(ii)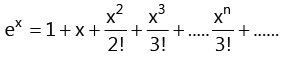 (iii)
(iii)
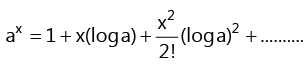 (iv)
(iv)
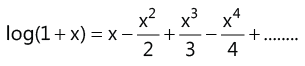 (v)
(v)
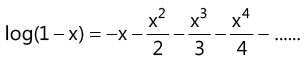 (vi)
(vi)
 (vii)
(vii)
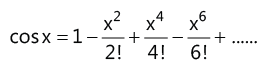 (viii)
(viii)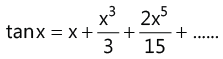
(ix)
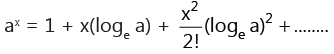 (x)
(x)
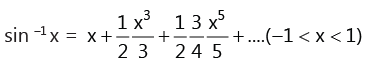 (xi)
(xi)
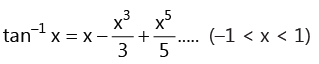
3. L’Hôpital’s rule
For functions f and g which are differentiable: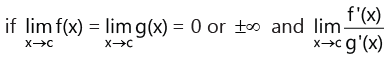 has a finite value then
has a finite value then 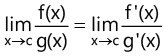
4. Common Indeterminate Forms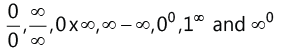
5. Differentiation
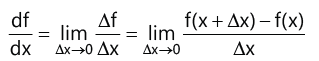 6. Continuity
6. Continuity
Function f(x) is continuous at x = a if
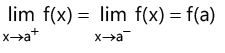
7. Differentiability
f(x) is said to be derivable or differentiable at x = a if f’(a+) = f’(a–) = finite quantity
8. Rolle’s theorem
If a function f defined on the closed interval [a, b] is continuous on [a, b] and derivable on (a, b) and f(a) = f(b), then there exists at least one real number c between a and b (a < c < b), such that f ‘ (c) = 0
9. Mean Value Theorem
If a function f defined on the closed interval [a, b], is continuous on [a, b] and derivable on (a, b), then there exists at least one real number c between a and b (a < c < b), such that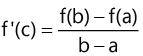
Solved Examples
Que1: The function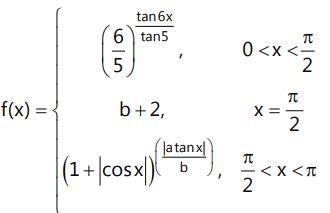 Determine the values of 'a' & 'b', if f is continuous at x = π/2
Determine the values of 'a' & 'b', if f is continuous at x = π/2Ans:
⇒ b + 2 = 1
b = – 1(as sin h > 0, for h → 0+ and cot h > 0, for h → 0+)
Now, this limit will be of the form equation for non zero values of a for a = 0,
Que2: Let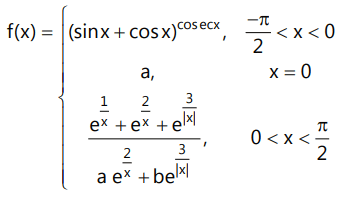 If f(x) is continuous at x = 0, then find the value of (a² + b²).
If f(x) is continuous at x = 0, then find the value of (a² + b²).
Ans: At x = 0
Que3: If
Examine the continuity of f(x) at x = 1.
Ans: In order to examine the continuity at x = 1, we are required to derive the definition of f(x) in the intervals x < 1, x > 1, and at x = 1, i.e., on and around x = 1.
Now, if 0 < x < 1,
Thus, we have
So, f(x) is not continuous at x = 1.
Que4: Which of the following functions defined below are NOT differentiable at the indicated point?
(a) 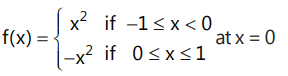 (b)
(b)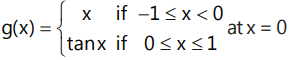
(c) 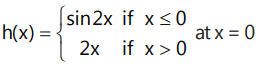 (d)
(d) 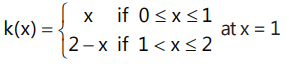
Ans: (d) A for f(x), at x = 0,
: LHD = RHD, f(x) is differentiable
(b) for g(x), at x = 0
: LHD = RHD, g(x) is differentiable
(c) for h(x) at x = 0
: LHD = RHD, h(x) is differentiable
(d) for k(x), at x = 1: LHD ≠ RHD, k(x) is not differentiable at x = 1
Que5: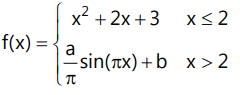 If f(x) is derivable ∀ x ∈ R, then
If f(x) is derivable ∀ x ∈ R, then
(a) 2a + bπ = 7
(b) b + 2π = 3
(c) 2a + bπ = 13
(d) None of these
Ans: (d) f(x) must also be continuous at x = 2
∴ LHL = RHL = Vf(x) = 2for derivability,
LHD = RHD(2x + 2) |x=2 = (a cos(πx)) |x=2 ⇒ 6 = a
∴ b = 11, a = 6
∴2a + bπ = 12 + 11π ≠ 7
b + 2π = 11 + 2π ≠ 3
2a + bπ = 12 + 11π ≠ 13
No correct option.
Que6: [x] denotes the greatest integer less than or equal to x. If f(x) = [sin(πx)] in (-1, 1) then f(x) is -
(a) Continuous at x = 0
(b) Continuous in (-1, 0) ∪ (0, 1)
(c) Differentiable in (-1, 1)
(d) None
Ans: (b) Function can be discontinuous at x = 0
At x = 0As x → 0⁻, [x] → -1, [sin(πx)] → -1
∴ LHL = -1 × -1 = 1As x → 0⁺, [x] → 0, [sin(πx)] → 0
∴ RHL = 0
: LHL ≠ RHL, f(x) is discontinuous at x = 0.
It can also be discontinuous at x = 1/2.
At x = 1/2continuous at x = -1/2 (∴ LHL = RHL)
At x = -1/2,∴ [sin(πx)] = -1
∴ LHL = -1 × -1 = 1∴ RHL = -1 × -1 = 1
∴ LHL = RHL, continuous at x = -1/2
f(x) is continuous in x ∈ (-1, 0) ∪ (0, 1)
Que7: The function f(x) = sin |x| is
(a) Continuous for all x
(b) Continuous only at certain points
(c) Differentiable at all points
(d) None of these
Ans:
for h → 0+
Now, |-h| = h, [h] = 0,
sin(-h) = –sin h < 0 ∀ sgn |sin(-h) ) | = –1
Que8: Function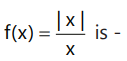
(a) Continuous everywhere
(b) Differentiable everywhere
(c) Differentiable everywhere except at x = 0
(d) None of these
Ans: (c)
∴ Function is discontinuous and not differentiable at x = 0
Que9: If 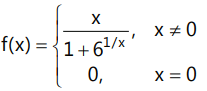
then the function f(x) is differentiable for -
(a) x ∈ R⁺
(b) x ∈ R
(c) x ∈ R₀
(d) None of these
Ans: (c)
∴ Function is not differentiable at x = 0
Que10: If
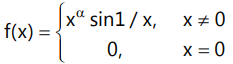 is differentiable at x = 0, then -
is differentiable at x = 0, then -
(a) α > 0
(b) α > 1
(c) α ≥ 1
(d) α ≥ 0
Ans: (b)
∴ for function to be differentiable
f'(0⁻) = f'(0⁺)
⇒ (-h)⁰⁻¹ = (h)⁰⁻¹
⇒ (-1)⁰⁻¹(h)⁰⁻¹ = (h)⁰⁻¹
∴ α = even ⇒ α > 1
|
176 videos|582 docs|160 tests
|
FAQs on Revision Notes: Continuity and Differentiability - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the definition of continuity in a function? |  |
| 2. How can we check the differentiability of a function? |  |
| 3. What are the types of discontinuity in functions? |  |
| 4. What is the relationship between continuity and differentiability? |  |
| 5. How do theorems like the Mean Value Theorem relate to continuity and differentiability? |  |