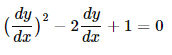Grade 12 Exam > Grade 12 Notes > Mathematics for Grade 12 > Reduction of Second Order Equation in Canonical Form
Reduction of Second Order Equation in Canonical Form | Mathematics for Grade 12 PDF Download
Second Degree Equation in Three Dimensions
- The general second degree Equation in three dimensions is
ax2 + by2 + cz + 2fyz + 2gzx + 2hxy + 2ux + 2vy + 2wz + d = 0 (4.8.1) - This may represent a plane or pair of planes (which, if not parallel, define a straight line), or an ellipsoid, paraboloid, hyperboloid, cylinder or cone.
- The Equation could, if convenient, be divided through by d (or any of the other constants), and there are in reality only nine independent constants. Therefore nine points in space are sufficient to determine the second degree surface on this they lie.
- If d is zero, the surface contains the origin. If u, v and w are all zero, and the surface is an ellipsoid, hyperbolic paraboloid or a hyperboloid, the origin is at the centre of the figure.
- If the figure is an elliptic paraboloid, the origin is at the vertex. If u, v w and d are all zero, the surface is a cone with the proviso mentioned in section 4.7. If a, b, c, f, g, h are all zero, the surface is a plane.
- Let us consider a particular example:
3x2 − 4y2 + 6z2 + 8yz − 2zx + 4xy + 14x − 10y − 4z + 5 = 0 (4.8.2)
What Kind of Surface is this?
We need to do two things.
- First we need to rotate the coordinate axes so that they are parallel to the figure axes. The Equation referred to the figure axes will have no terms in yz, zx or xy. Then we need to translate the axes so that the origin is at the centre of the figure (or at the vertex, if it is an elliptical paraboloid).
- Mathematically, we need to find the eigenvectors of the matrix
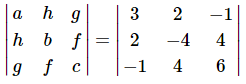 (4.8.3)
(4.8.3) - Some readers will readily know how to do this. Others may not, and may not even be quite certain what an eigenvector is. Section 4.9 may be of interest to either group of readers. In any case, the eigenvectors are found to be
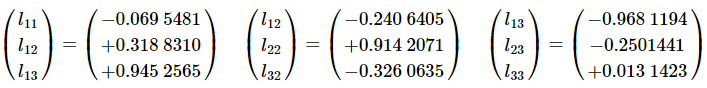 (4.8.1)
(4.8.1)
with corresponding eigenvalues 7.422 7590, 5.953 0969, 3.530 3380. - The elements of the eigenvectors are the direction cosines of the present coordinate axis with respect to the figure axes. To express the Equation to the surface relative to coordinate axes that are parallel to the figure axes, we replace
- x by l11x + l12y + l13z (4.8.2)
- y by l21x + l22y + l23z (4.8.3)
- z by l31x + l32y + l33z (4.8.4)
- This will make the terms in yz, zx and xy vanish; this should be checked numerically, particularly as it is easy to rotate the axes in the wrong sense. When the substitutions are made, the Equation is found to be
7.422 7590x2 − 5.9530969y2 + 3.530 3380z2 − 7.9430994x − 11.2067840y − 11.1047998z + 5 = 0. (4.8.4) - Notice that there are now no terms in yz, zx or xy.
Now we need to translate the origin of coordinates to the centre of the figure (or to the vertex if it is an elliptic paraboloid). It will readily be seen that this can be done by substituting - x − α for x (4.8.5)
- y − β for y (4.8.6)
- z − γ for z (4.8.7)
- where
- α = (coefficient of x)/(twice the coefficient of x2) = −0.535 050 336 (4.8.8)
- β = (coefficient of y)/(twice the coefficient of y2) = +0.941 256 643 (4.8.9)
- γ = (coefficient of z)/(twice the coefficient of z2) = −1.572 767 224 (4.8.10)
- The Equation then becomes
7.422 7590x2 − 5.953 0969y2 + 3.530 3380z2 − 0.583 3816 = 0 (4.8.11) - or
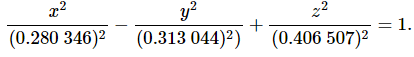 (4.8.12)
(4.8.12)- The surface is a hyperboloid of one sheet, elliptical in any y = constant cross-section.
- The surfaces described by second-degree Equations in three dimensions - ellipsoids, paraboloids, hyperboloids, cones and cylinders - are generally called quadric surfaces. The surface described by the Equation
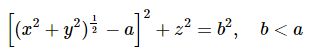 (4.8.13)
(4.8.13)
is not one of the quadric surfaces. If the square root is isolated and squared, the resulting Equation will contain terms of degree four. The surface is a fairly familiar one, and the reader should try to imagine what it is. Failing that, if your computer skills are up to it, you might try to draw the surface in three-dimensional space. The only hint I give is to suggest that you put y=0 in Equation ??? to see what the section is in the z-x plane.
Reduction of Second Order Equation in Canonical Form
Q: Reduce the following equation to canonical form and to find general solution.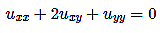
Canonical form as 4uηη + 3uξη = 0. Is it right?
Ans: The Characteristic equation
gives only one characteristic curve,
y − x = constant.
So, taking ξ = y − x and η = y , the given equation reduces to uηη = 0.
The document Reduction of Second Order Equation in Canonical Form | Mathematics for Grade 12 is a part of the Grade 12 Course Mathematics for Grade 12.
All you need of Grade 12 at this link: Grade 12
|
270 videos|267 docs|155 tests
|
FAQs on Reduction of Second Order Equation in Canonical Form - Mathematics for Grade 12
| 1. What is a second degree equation in three dimensions? |  |
Ans. A second degree equation in three dimensions is a polynomial equation of the form Ax^2 + By^2 + Cz^2 + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0, where A, B, C, D, E, F, G, H, I, and J are constants. It represents a conic section or quadric surface in 3D space, which can take forms such as ellipsoids, hyperboloids, or paraboloids depending on the values of the coefficients.
| 2. How can a second degree equation be reduced to canonical form? |  |
Ans. To reduce a second degree equation to canonical form, one typically performs a series of transformations including completing the square for the quadratic terms and using rotation and translation to eliminate mixed terms (like xy, xz, or yz). The goal is to express the equation in a simpler form that clearly identifies the type of quadric surface it represents, such as x^2/a^2 + y^2/b^2 + z^2/c^2 = 1 for an ellipsoid.
| 3. What are the types of quadric surfaces represented by second degree equations? |  |
Ans. The types of quadric surfaces that can be represented by second degree equations include ellipsoids, hyperboloids, paraboloids, cones, and planes. Each surface type is determined by the signs and relationships of the coefficients in the equation, and understanding their geometry is crucial for solving problems in three-dimensional space.
| 4. Why is the reduction to canonical form important in mathematics? |  |
Ans. Reducing second degree equations to canonical form is important because it simplifies the analysis of the geometric properties of the surfaces represented by these equations. It facilitates easier identification of the surface type, simplifies calculations, and helps in visualizing the relationships between different variables in three-dimensional space, which is particularly useful in fields such as physics and engineering.
| 5. What methods are commonly used to reduce second degree equations to canonical form? |  |
Ans. Common methods for reducing second degree equations to canonical form include algebraic techniques such as completing the square, using linear transformations to diagonalize the associated matrix of coefficients, and applying rotation to eliminate the cross-product terms. These methods help in systematically transforming the equation into a recognizable and standard format.
Related Searches