Q.1. Compare the fractions:
(i) 5/8 and 7/12
(ii) 5/9 and 11/15
(iii) 11/12 and 15/16
Ans. We have the following:
(i) 5/8 and 7/12
By cross multiplication, we get:
5 × 12 = 60 and 7 × 8 = 56
However, 60 > 56
∴ 5/8 > 7/12
(ii) 5/9 and 11/15
By cross multiplication, we get:
5 × 15 = 75 and 9 × 11 = 99
However, 75 < 99
∴ 5/9 < 11/15
(iii) 11/12 and 15/16
By cross multiplication, we get:
11 × 16 = 176 and 12 × 15 = 180
However, 176 < 180
∴ 11/12 < 15/16
Q.2. Arrange the following fractions in ascending order:
(i) 3/4, 5/6, 7/9, 11/12
(ii) 4/5, 7/10, 11/15, 17/20
Ans. (i) The given fractions are 3/4, 5/6, 7/9 and 11/12.
LCM of 4, 6, 9 and 12 = 36
Now, let us change each of the given fractions into an equivalent fraction with 72 as its denominator.
3/4 = (3×9) / (4×9) = 27/36
5/6 = (5×6) / (6×6) = 30/36
7/9 = (7×4) / (9×4) = 28/36
11/12 = (11×3) / (12×3) = 33/36
Clearly, 27/36 < 28/36 < 30/36 < 33/36
Hence, 3/4 < 7/9 < 5/6 < 11/12
∴ The given fractions in ascending order are 3/4, 7/9, 5/6 and 11/12
(ii) The given fractions are: 4/5, 7/10, 11/15 and 17/20.
LCM of 5, 10, 15 and 20 = 60
Now, let us change each of the given fractions into an equivalent fraction with 60 as its denominator.
4/5 = (4×12) / (5×12) = 48/60
7/10 = (7×6) / (10×6) = 42/60
11/15 = (11×4) / (15×4) = 44/60
17/20 = (17×3) / (20×3) = 51/60
Clearly, 42/60 < 44/60 < 48/60 < 51/60
Hence, 7/10 < 11/15 < 4/5 < 17/20
∴ The given fractions in ascending order are
7/10, 11/15, 4/5 and 17/20
Q.3. Arrange the following fractions in descending order:
(i) 3/4, 7/8, 7/12, 17/24
(ii) 2/3, 3/5, 7/10, 8/15
Ans. We have the following:
(i) The given fractions are 3/4, 7/8, 7/12 and 17/24.
LCM of 4,8,12 and 24 = 24
Now, let us change each of the given fractions into an equivalent fraction with 24 as its denominator.
3/4 = (3×6) / (4×6) = 18/24
7/8 = (7×3) / (8×3) = 21/24
7/12 = (7×2 / 12×2) = 14/24
17/24 = (17×1) / (24×1) = 17/24
Clearly, 21/24 > 18/24 > 17/24 > 14/24
Hence, 7/8 > 3/4 > 17/24 > 7/12
∴ The given fractions in descending order are 7/8, 3/4, 17/24 and 7/12.
(ii) The given fractions are 2/3, 3/5, 7/10 and 8/15.
LCM of 3,5,10 and 15 = 30
Now, let us change each of the given fractions into an equivalent fraction with 30 as its denominator.
2/3 = (2×10) / (3×10) = 20/30
3/5 = (3×6) / (5×6) = 18/30
7/10 = (7×3) / (10×3) = 21/30
8/15 = (8×2) / (15×2) = 16/30
Clearly, 21/30 > 20/30 > 18/30 > 16/30
Hence, 7/10 > 2/3 > 3/5 > 8/15
∴ The given fractions in descending order are 7/10, 2/3, 3/5 and 8/15.
Q.4. Reenu got 2/7 part of an apple while Sonal got 4/5 part of it. Who got the larger part and by how much?
Ans. We will compare the given fractions 2/7 and 4/5 in order to know who got the larger part of the apple.
We have,
By cross multiplication, we get: 2 × 5 = 10 and 4 × 7 = 28
However, 10 < 28
∴ 2/7 < 4/5
Thus, Sonal got the larger part of the apple.
Now, 4/5 - 2/7 = (28-10) / 35 = 18/35
∴ Sonal got 18/35 part of the apple more than Reenu.
Q.5. Find the sum
(i) 5/9 + 3/9
(ii) 8/9 + 7/12
(iii) 5/6 + 7/8
(iv) 7/12 + 11/16 + 9/24
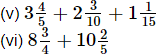
Ans. (i) 5/9 + 3/9 = 8/9
(ii) 8/9 + 7/12
= 32/36 + 21/36 [∵ LCM of 9 and 12 = 36]
= (32+21) / 36
= 53/36
=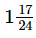
(iii) 5/6 + 7/8 = 20/24 + 21/24 [∵ LCM of 6 and 8 = 24]
= (20+21) / 24
= 41/24
=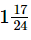
(iv) 7/12 + 11/16 + 9/24
28/48 + 33/48 + 18/48 [∵ LCM of 12, 16 and 24 = 48]
= (28+33+18) / 48
= 79/48
=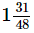
(v)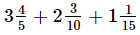 = 19/5 + 23/10 + 16/15
= 19/5 + 23/10 + 16/15
= 114/30 + 69/30 + 32/30 [∵ LCM of 5, 10 and 15 = 30]
= (114+69+32) / 30
= 215/30
= 
(vi)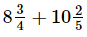
= 35/4 + 52/5
= 175/20 + 208/20 [∵ LCM of 4 and 5 = 20]
= (175+208) / 20
= 383/20
=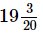
Q.6. Find the difference:
(i) 5/7 - 2/7
(ii) 5/6 - 3/4
(iii)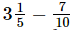
(iv) 7 - 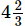
(v)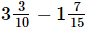
(vi)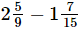
Ans. (i) 5/7 - 2/7 = (5-2) / 7 = 3/7
(ii) 5/6 - 3/4 = 10/12 - 9/12 [∵ LCM of 6 and 4 = 12]
= (10-9) / 12
= 1/12
(iii)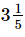 - 7/10 = 16/5 - 7/10
- 7/10 = 16/5 - 7/10
= 32/10 - 7/10 [∵ LCM of 5 and 10 = 10]
= (32-7) / 10
= 25/10
= 5/2
=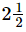
(iv) 7 -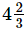
= 7/1 - 14/3
= (21-14) / 3 [∵ LCM of 1 and 3 = 3]
= 7/3
=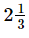
(v)
= 33/10 - 22/15
= (99-44) / 30 [∵ LCM of 10 and 15 = 30]
= 55/30
= 11/6
=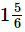
(vi)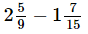
= 23/9 - 22/15
= (115-66) / 45 [∵ LCM of 9 and 15 = 45]
= 49/45
=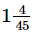
Q.7. Simplify:
(i) 2/3 + 5/6 - 1/9
(ii) 8 - 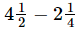
(iii)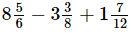
Ans. (i) 2/3 + 5/6 - 1/9
= (12+15-2) / 18 [∵ LCM of 3, 6 and 9 = 18]
= (27-2) / 18
= 25/18
=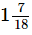
(ii) 8 -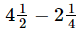
= 8/1 - 9/2 - 9/4
= (32-18-9) / 4 [∵ LCM of 1, 2 and 4 = 4]
= (32-27) / 4
= 5/4
=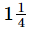
(iii)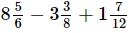
= 53/6 - 27/8 + 19/12
= (212-81+38) / 24 [∵ LCM of 6, 8 and 12 = 24]
= (250-81) / 24
= 169/24
=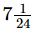
Q.8. Aneeta bought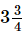 kg apples and
kg apples and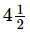 kg guava. What is the total weight of fruits purchased by her?
kg guava. What is the total weight of fruits purchased by her?
Ans. Total weight of fruits bought by Aneeta =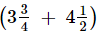 kg
kg
Now, we have:
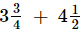 = 15/4 + 9/2
= 15/4 + 9/2
= (15 + 18) / 4 [∵ LCM of 2 and 4 = 4]
= (15 + 18) / 4
= 33/4
=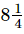
Hence, the total weight of the fruits purchased by Aneeta is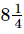 kg.
kg.
Q.9. A rectangular sheet of paper is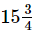 cm long and
cm long and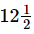 cm wide. Find its perimeter.
cm wide. Find its perimeter.
Ans. We have:
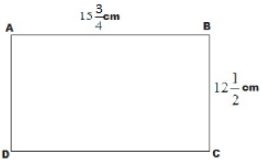
Perimeter of the rectangle ABCD = AB + BC + CD +DA
=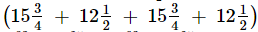 cm
cm
= (63/4 + 25/2 + 63/4 + 25/2) cm
= (63 + 50 + 63 + 50) / 4 cm [∵ LCM of 2 and 4 = 4]
= (226 / 4) cm
=(113 / 2) cm
=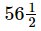 cm
cm
Hence, the perimeter of ABCD is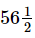 cm
cm
Q.10. A picture is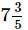 cm wide. How much should it be trimmed to fit in a frame
cm wide. How much should it be trimmed to fit in a frame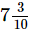 cm wide?
cm wide?
Ans. Actual width of the picture =  cm = 38/5 cm
cm = 38/5 cm
Required width of the picture =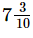 cm = 73/10 cm
cm = 73/10 cm
∴ Extra width = (38/5−73/10)cm
= (76−73) / 10 cm [∵ LCM of 5 and 10 is 10]
= 3/10 cm
Hence, the width of the picture should be trimmed by 3/10 cm.
Q.11. What should be added to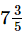 to get 18?
to get 18?
Ans. Required number to be added = 18−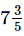
=18/1−38/5
= (90−38) / 5 [∵ LCM of 1 and 5 = 5]
= 52/5 =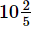
Hence, the required number is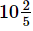
Q.12. What should be added to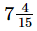 to get
to get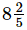 ?
?
Ans. Required number to be added =
= 42/5−109/15
= (126−109)/15 [∵ LCM of 5 and 15 = 15]
= 17/15
=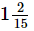
Hence, the required number should be 12151215.
Q.13. A piece of wire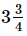 m long broke into two pieces. One piece is
m long broke into two pieces. One piece is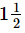 m long. How long is the other piece?
m long. How long is the other piece?
Ans. Required length of other piece of wire = 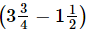 m
m
=(15/4−3/2) m
= ((15−6)/4) m [∵ LCM of 4 and 2 = 4]
= 9/4 m
=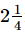 m
m
Hence, the length of the other piece of wire is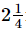 m.
m.
Q.14. A film show lasted of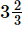 hours. Out of this time
hours. Out of this time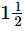 hours was spent on advertisements. What was the actual duration of the film?
hours was spent on advertisements. What was the actual duration of the film?
Ans. Actual duration of the film = ( −
−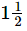 )hours
)hours
= (11/3−3/2) hours
= (22−9)/ 6 hours [∵ LCM of 3 and 2 = 6]
= 13/6 hours
= 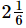 hours
hours
Hence, the actual duration of the film was 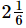 hours
hours
Q.15. Of 2/3 and 5/9, which is greater and by how much?
Ans. First we have to compare the fractions: 2/3 and 5/9.
By cross multiplication, we have:
2 × 9 = 18 and 5 × 3 = 15
However, 18 > 15
∴2/3 > 5/9
So, 2/3 is larger than 5/9.
Now, 2/3−5/9
= (6−5) / 9 [∵ LCM of 3 and 9 = 9]
= 1/9
Hence, 2/3 is 1/9 part more than 5/9.
Q.16. The cost of a pen is Rs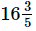 and that of a pencil is Rs
and that of a pencil is Rs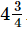 . Which costs more and by how much?
. Which costs more and by how much?
Ans. First, we have to compare the cost of the pen and the pencil.
Cost of the pen = Rs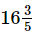 = Rs 83/5
= Rs 83/5
Cost of the pencil = Rs 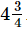 = Rs 19/4
= Rs 19/4
Now, we have to compare fractions 83/5 and 19/4.
By cross multiplication, we get: 83 × 4 = 332 and 19 × 5 = 95
However, 332 > 95
∴ 83/5 > 19/4
So, the cost of pen is more than that of the pencil.
Now, Rs (83/5 − 19/4)
= Rs (332 − 95) / 20 [∵ LCM of 4 and 5 = 20]
= Rs 237
= Rs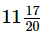
∴ The pen costs Rs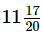 more than the pencil.
more than the pencil.
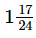
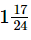
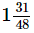
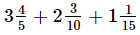 = 19/5 + 23/10 + 16/15
= 19/5 + 23/10 + 16/15
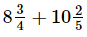
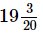
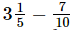
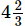
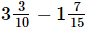
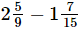
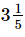 - 7/10 = 16/5 - 7/10
- 7/10 = 16/5 - 7/10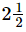
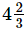
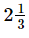

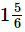
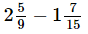
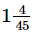
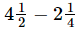
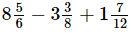
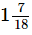
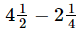
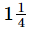
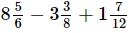
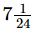
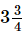 kg apples and
kg apples and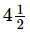 kg guava. What is the total weight of fruits purchased by her?
kg guava. What is the total weight of fruits purchased by her?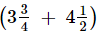 kg
kg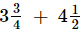 = 15/4 + 9/2
= 15/4 + 9/2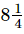
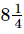 kg.
kg.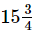 cm long and
cm long and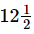 cm wide. Find its perimeter.
cm wide. Find its perimeter.
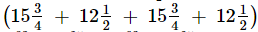 cm
cm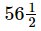 cm
cm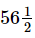 cm
cm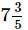 cm wide. How much should it be trimmed to fit in a frame
cm wide. How much should it be trimmed to fit in a frame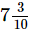 cm wide?
cm wide? cm = 38/5 cm
cm = 38/5 cm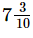 cm = 73/10 cm
cm = 73/10 cm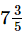 to get 18?
to get 18?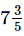
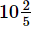
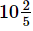
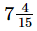 to get
to get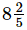 ?
?
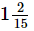
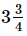 m long broke into two pieces. One piece is
m long broke into two pieces. One piece is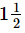 m long. How long is the other piece?
m long. How long is the other piece?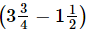 m
m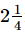 m
m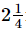 m.
m.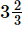 hours. Out of this time
hours. Out of this time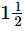 hours was spent on advertisements. What was the actual duration of the film?
hours was spent on advertisements. What was the actual duration of the film? −
−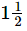 )hours
)hours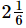 hours
hours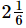 hours
hours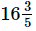 and that of a pencil is Rs
and that of a pencil is Rs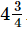 . Which costs more and by how much?
. Which costs more and by how much?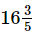 = Rs 83/5
= Rs 83/5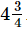 = Rs 19/4
= Rs 19/4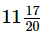
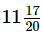 more than the pencil.
more than the pencil.

























