Points to Remember: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
| Table of contents |

|
| Introduction |

|
| Observing Similarity in Change |

|
| Ratios |

|
| Proportional Ratios |

|
| Ancient Wisdom – Āryabhaṭa’s Rule of Three |

|
| Sharing in Ratios |

|
| Unit Conversions |

|
Introduction
In daily life, digital images are often resized or rotated.
Some resized images look similar (same shape, different size), while others look distorted (shape changes).
The difference depends on whether the width and height change by the same factor or not.
Observing Similarity in Change
Similar images → Width and height change by the same multiplication factor.
Distorted images → Width and height change by different factors.

Examples: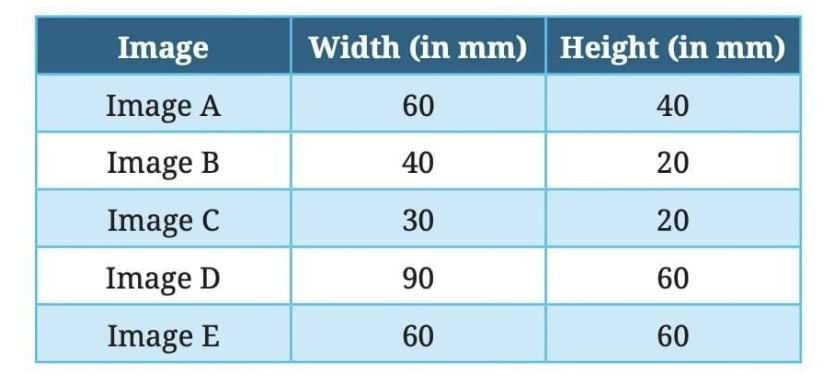
Image A vs. C: Both width & height reduced by ½ → Similar.
Image A vs. B: Width factor = 2/3, Height factor = ½ → Distorted.
Image A vs. D: Both width & height increased by 3/2 → Similar.
Image A vs. E: Width factor = 1, Height factor = 3/2 → Distorted.
Conclusion:
Proportional Change (same factor) → Shape remains same.
Non-proportional Change (different factors) → Shape looks distorted.
Ratios
Definition: A ratio compares two quantities of the same kind.
Form: a : b → “a is to b”.
Example: Width : Height of Image A = 60 : 40.
Simplifying Ratios
Divide both terms by their HCF.
Example:
60 : 40 → HCF = 20 → 3 : 2.
90 : 60 → HCF = 30 → 3 : 2.
Ratios in simplest form make comparisons easier.
Proportional Ratios
Two ratios are proportional if they simplify to the same simplest form.
Written as:
a : b :: c : d (read as “a is to b as c is to d”).
Rule: If a : b = c : d, then ad = bc (cross multiplication).
Examples:
3 : 4 and 72 : 96 → Both simplify to 3 : 4 → Proportional.
3 : 2 and 2 : 1 → Not proportional.
Ancient Wisdom – Āryabhaṭa’s Rule of Three
Terms:
Pramāṇa → Measure (a)
Phala → Result (b)
Ichchhā → Desired measure (c)
Ichchhāphala → Required result (d)
Method:
d = (Phala × Ichchhā) ÷ Pramāṇa
→ Same as modern proportion formula.
Sharing in Ratios
To divide a quantity in a ratio m : n:
Add the parts (m + n).
Find value of one part = Total ÷ (m + n).
Multiply by m and n.
Examples:
Divide 12 in 3 : 1 → 9 and 3.
Divide 42 in 4 : 3 → 24 and 18.
Divide 60 in 2 : 3 → 24 and 36.
Unit Conversions
Always use same units before comparing ratios.
Key Conversions:
Length: 1 m = 3.281 ft
Area: 1 m² = 10.764 ft²; 1 acre = 43,560 ft²; 1 hectare = 10,000 m² = 2.471 acres
Volume: 1 mL = 1 cc; 1 L = 1,000 mL
Temperature:
F = (9/5 × C) + 32
C = 5/9 × (F − 32)
Always convert before simplifying ratios or checking proportion.
|
20 videos|122 docs|11 tests
|
FAQs on Points to Remember: Proportional Reasoning-1 - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are ratios, and how are they used in proportional reasoning? |  |
| 2. Can you explain Āryabhaṭa’s Rule of Three and its significance in historical mathematics? |  |
| 3. How do you share quantities in ratios, and what practical applications does this have? |  |
| 4. What is the importance of unit conversions in understanding ratios? |  |
| 5. What are some key points to remember about proportional reasoning? |  |














