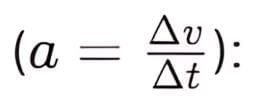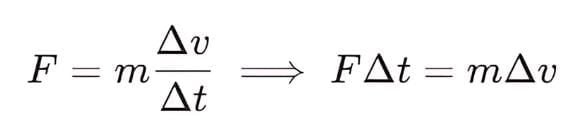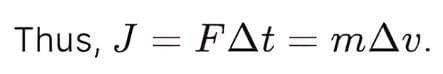Newton's Laws of Motion | Physics Class 11 - NEET PDF Download
Introduction
Newton's laws of motion are three important laws that explain how objects move. These laws were discovered by Sir Isaac Newton, a famous scientist, in the 17th century. They help us understand why things move or stay still and how forces like pushes and pulls affect objects. These laws are used in many areas of science and everyday life, from driving a car to playing sports. Understanding these laws gives us a clear picture of the basic rules that govern all motion in the universe.
When you travel in a hilly area, while taking a right turn you tend to fall towards the left side. Similarly, when brakes are applied to a car, you tend to fall forward. Why does this happen? These questions can be easily answered with the understanding of Newton's First Law of Motion or what we also know as 'Law of Inertia'.
 Law of Inertia
Law of Inertia
We have read about the Aristotle fallacy, in which an external force is always required to keep a body in motion. This was proved wrong when the concept of inertia came into the picture. Galileo established the concept of inertia through two key experiments.
Galileo’s Free Fall Experiment
If an object is released from rest and gains speed at a steady rate (as it would in free-fall or when rolling down an inclined plane), then the total distance, s, traveled by the object is proportional to the time squared needed for that travel.
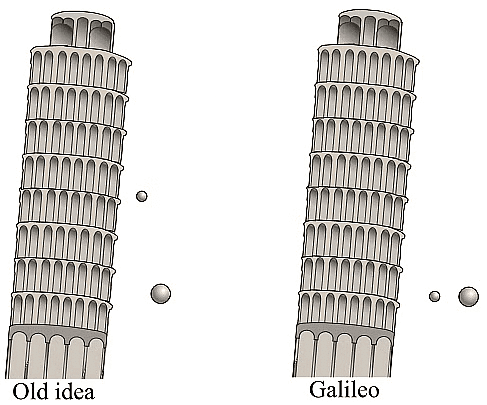 Galileo's experiment challenged Aristotle's gravity theory, proving that objects of different masses fall at the same acceleration.
Galileo's experiment challenged Aristotle's gravity theory, proving that objects of different masses fall at the same acceleration.
- Galileo attempted to decelerate the motion of a falling object with a ball rolling down an inclined plane. Since free-falling is basically equivalent to a completely vertical ramp, he assumed that a ball rolling down a ramp would speed up in the exact same way as a falling ball would.
- Using a water clock, Galileo measured the time it took for the rolling ball to reach a known distance down the inclined plane.
- After several trials, it was observed that the time it took for the ball to roll the entire length of the ramp was equal to double the amount of time it took for the same ball to only roll a quarter of the distance.
- In short, the distance traveled by the ball is proportional to the square of the time taken.Through this experiment, Galileo concluded that:
Galileo's Inclined Plane Experiment
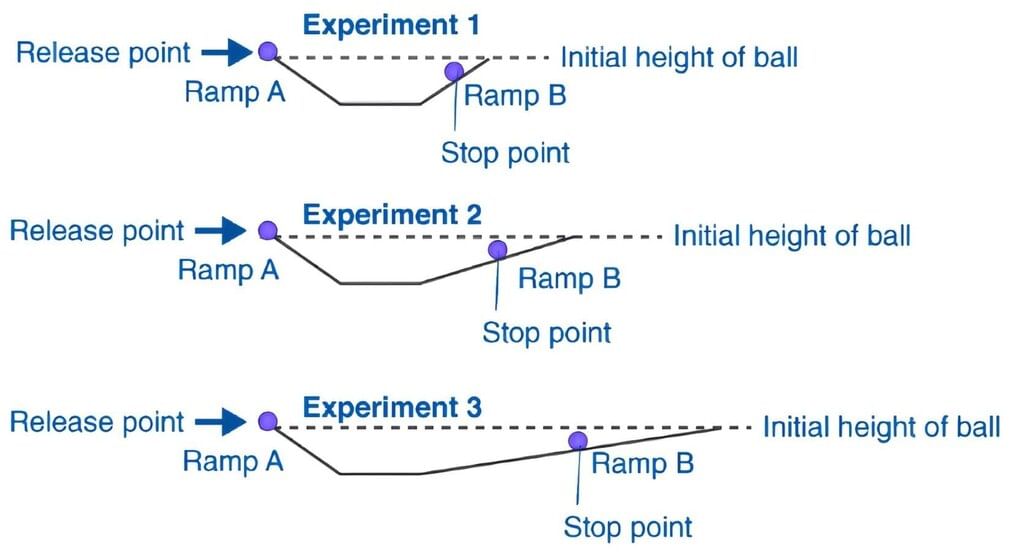 Galileo's Inclined Plane Experiment
Galileo's Inclined Plane Experiment
- He concluded that, if the planes are smooth, the final height achieved by the ball is nearly the same as the height through which it rolls from the first plane.
- In the second experiment, the slope of the second inclined plane was decreased and the ball was made to roll again.
- Here, the ball still reaches the same height, and in doing so, it travels a longer distance.
- According to the observation, when the slope of the second plane was decreased to zero, that is, the plane was made horizontal, and the ball was supposed to travel an infinite distance, that is the motion never ceases.
- However, due to friction, the object eventually comes to rest. after a finite distance but under ideal conditions, when there is no friction, the ball would continue to move with constant velocity on the horizontal plane.
- With this conclusion, the statements of Aristotle were proved wrong. He concluded that it was incorrect to assume that a net force was needed to keep a body in uniform motion and that the state of rest and state of uniform motion as equivalent.
Types of Inertia
Following are the three types of inertia: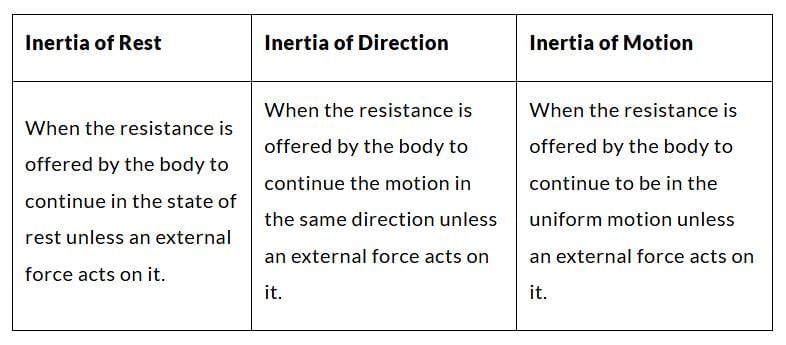
 Inertia of Rest
Inertia of Rest Inertia of Motion
Inertia of Motion
 Inertia of Direction
Inertia of Direction
Newton’s First Law of Motion
Newton’s first law states that
A body remains in the state of rest or uniform motion in a straight line unless and until an external force acts on it.
Putting Newton’s 1st law of motion in simple words, a body will not start moving until and unless an external force acts on it. Once it is set in motion, it will not stop or change its velocity until and unless some force acts upon it once more. The first law of motion is sometimes also known as the law of inertia.
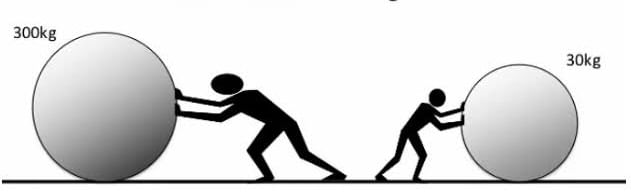 Inertia depends on mass
Inertia depends on mass
There are two conditions on which the 1st law of motion is dependent:
- Objects at rest: When an object is at rest velocity (v= 0) and acceleration (a = 0) are zero. Therefore, the object continues to be at rest.
- Objects in motion: When an object is in motion, velocity is not equal to zero (v ≠ 0) while acceleration (a = 0) is equal to zero. Therefore, the object will continue to be in motion with constant velocity and in the same direction.
What is an External Force?
An external force is a push or pull applied by something outside the object or system being studied.
These forces are caused by external agents. Examples of external forces are friction, normal force, and air resistance.
Illustration of the First Law of Motion
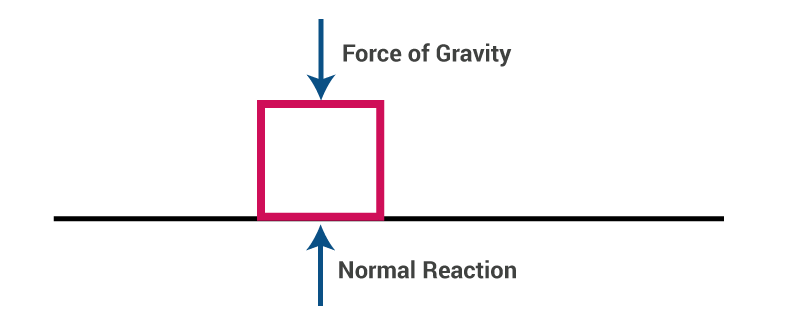
- Let us take a block on a smooth surface. By smooth, we mean that there is no friction acting on the surface.
- The block is at rest, that is, it is not moving. Now, let us examine the forces acting on the block.
- The only forces acting on the block are the force of gravity and the normal reaction by the surface. There is no force acting on it in the horizontal direction.
- Since the forces in the vertical direction are equal to each other in magnitude, they cancel each other out, and hence there is no external force on the block.
- Since this block is at rest, we can say that it confirms Newton’s first law of Motion.
Now, if we apply a constant force F on the block in a horizontal direction, it will start moving with some constant acceleration, in the direction of the applied force.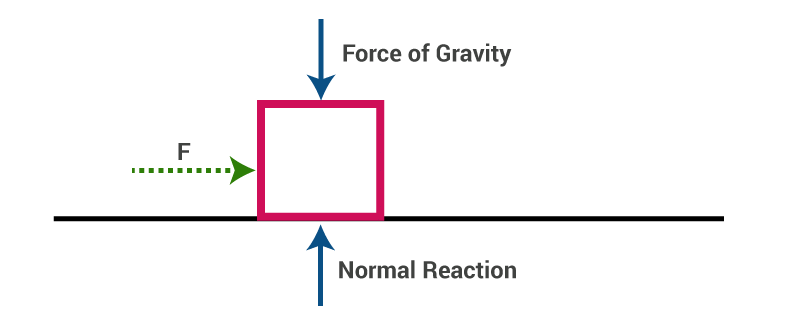
Thus, the first law of motion is confirmed again.
Note: Newton’s laws are valid only in inertial frames of reference.
Applications of Inertia
- When a bus or a train starts suddenly, the passenger standing inside it falls backward: It happens because the feet of the passenger being in contact with the floor of the bus come in motion along with the bus but the upper part of the body remains at rest due to inertia of rest. Hence the passenger falls backward.
- When a tree is vigorously shaken, some of the leaves fall from the tree: When the branch of a tree is vigorously shaken, the branch comes in motion as the force is applied to the branch. But the leaves want to remain at rest due to the inertia of rest and fall down.
- The carpet is beaten with a stick to remove the dust particles: When a carpet is beaten with a stick, the carpet comes in motion but the dust particles remain at rest due to inertia of rest.
Solved Questions
Q.1. What are the major concepts involved in the topic?
Ans: The major concepts involve the Frame of reference, Newton’s First law of motion (Law of Inertia), Newton’s Second law of motion, Newton’s Third law of motion (For every action there is an equal and opposite reaction), and constraint equations.
Q.2. What do we understand by a free body diagram?
Ans: A free body diagram represents all the forces acting on the body. For example,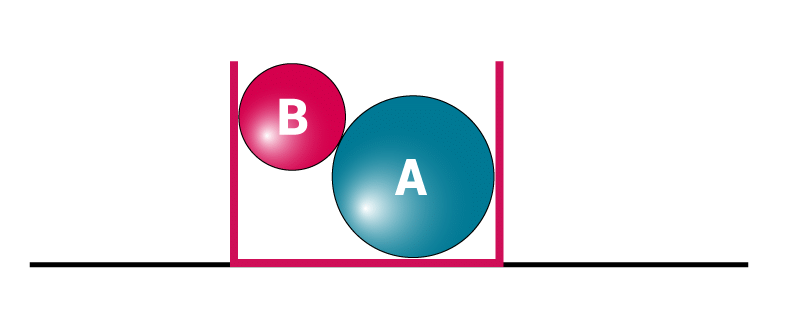
The Free Body Diagram (FBD) for sphere B is shown below.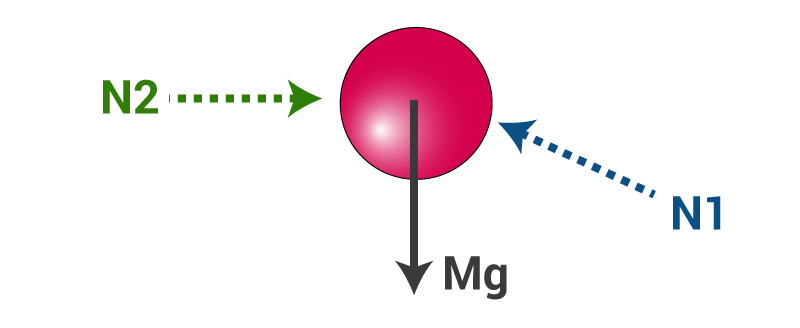
Q.3. What are the steps to solve a problem on Newton’s laws of motion?
Ans: Let us take the following example,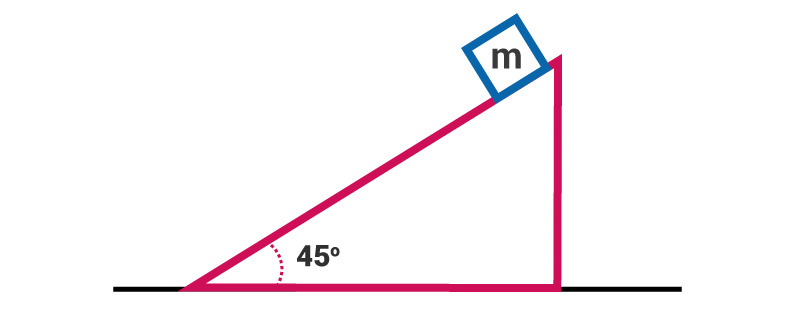
The wedge is fixed, and we need to find the acceleration of the block of mass m along the incline.
Step 1: Draw the F.B.D of the block,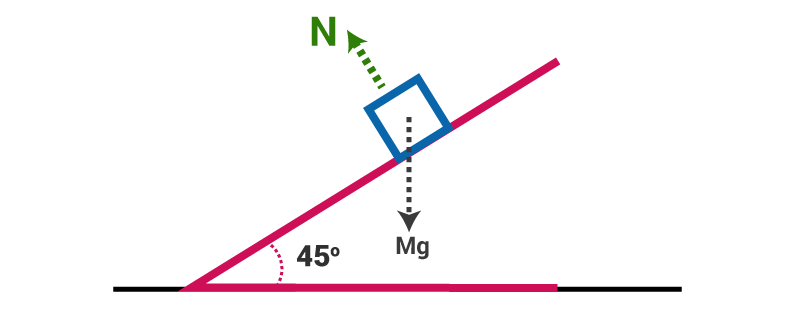
Step 2: Writing the force equation, taking our own axis, in this case, we take two axes, one along the plane and the other perpendicular to it.
Fincline = mg sin45∘
VFNormal = N – mg cos45∘
Step 3: Calculating acceleration using the second law of motion mg sin45∘ = ma
a = g sin 45∘
Q.4. What is the constraint equation?
Ans: When the motion of one body is governed by another or in other words when the motion of two or more bodies is interlinked. The equation governing such motion is known as the constraint equation. For example: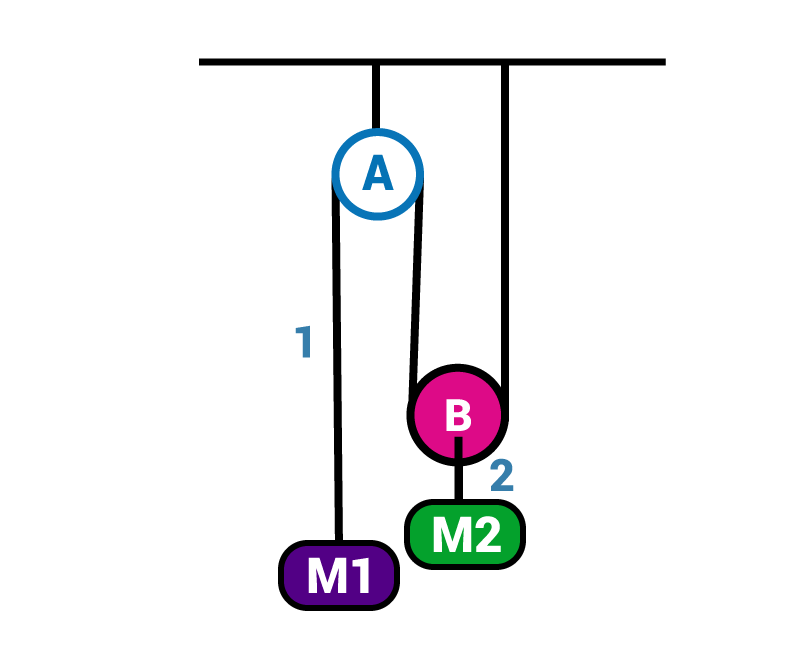
If we draw the FBD and write equations we will get,
M1.g – T = M1.a1
2T – M2.g = M2.a2
We can see there are two equations and three unknowns: a1, a2 and T. So, we need one more equation and that will be the constraint equation.
What is Newton’s Second Law of Motion?
Force is equal to the rate of change of momentum. For a constant mass, force equals mass times acceleration.
Newton’s second law of motion, unlike the first law of motion pertains to the behavior of objects for which all existing forces are unbalanced. The second law of motion is more quantitative and is used extensively to calculate what happens in situations involving a force.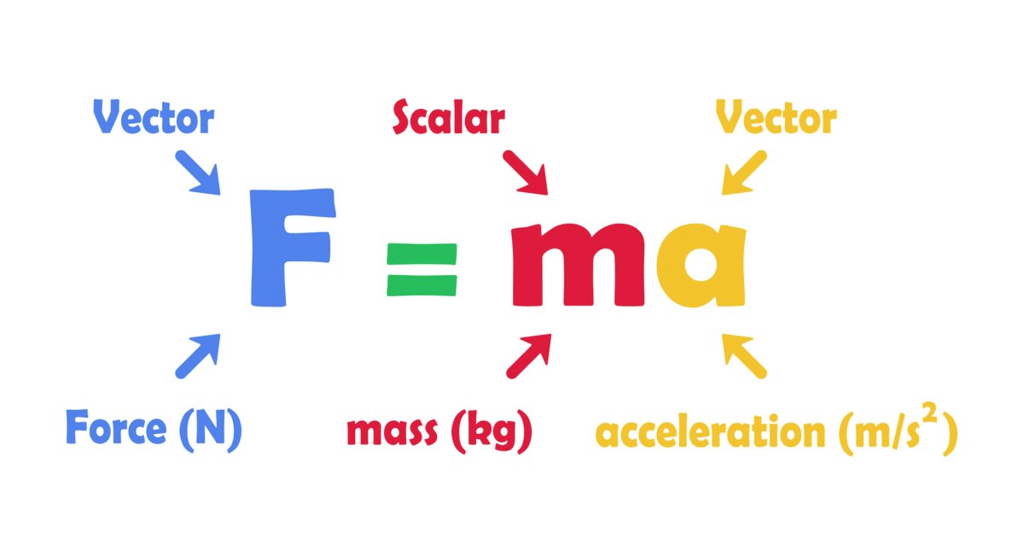 Representation of Second Law of Motion
Representation of Second Law of Motion
Defining Newton’s Second Law of Motion
- Newton’s second law states that the acceleration of an object depends upon two variables – the net force acting on the object and the mass of the object.
- The acceleration of the body is directly proportional to the net force acting on the body and inversely proportional to the mass of the body.
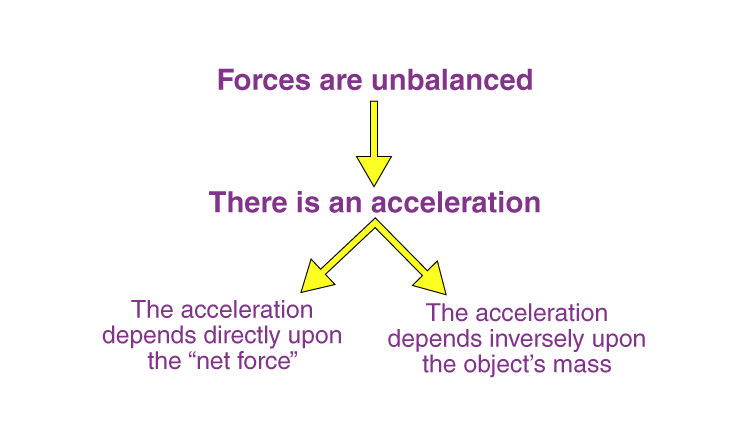
- This means that as the force acting upon an object is increased, the acceleration of the object is increased. Likewise, as the mass of an object is increased, the acceleration of the object is decreased.
Newton’s second law can be formally stated as:
The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.
This statement is expressed in equation form as:
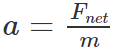
The above equation can be rearranged to a familiar form as:
F = ma
Since force is a vector, Newton’s second law can be written as: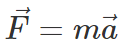
The equation shows that the direction of the total acceleration vector points in the same direction as the net force vector.
Deriving Newton’s Second Law
1. For Changing Mass
- Let us assume that we have a car at a point (0) defined by location X0 and time t0. The car has a mass m0 and travels with a velocity v0.
- After being subjected to a force F, the car moves to point 1 which is defined by location X1 and time t1. The mass and velocity of the car change during the travel to values m1 and v1.
- Newton’s second law helps us determine the new values of m1 and v1 if we know the value of the acting force.
- Taking the difference between point 1 and point 0, we get an equation for the force acting on the car as follows:
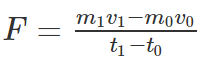
In everyday scenarios like cars, mass is usually constant, since fuel burned over short time intervals doesn’t significantly change the total mass.
For rockets (like bottle rockets), mass changes due to expelled fuel, so we must use momentum-based analysis (i.e., variable mass systems).
2. For Constant Mass
- For a constant mass, Newton’s second law can be equated as follows:
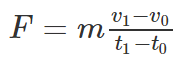
- We know that acceleration is defined as the change in velocity divided by the change in time. The second law then reduces to a more familiar form as follows: F = ma
- The above equation tells us that an object will accelerate if it is subjected to an external force and the amount of force is directly proportional to the acceleration and inversely proportional to the mass of the object.
What is a Net Force?
- A net force Σ F is the sum of all forces acting on a body. More precisely, it is the vector sum of all forces acting on a body.
 Force on a Body
Force on a Body - Consider two forces of magnitude 30 N and 20 N that are exerted to the right and left, respectively, on the horse shown in the picture.
- If we assume the rightward direction as positive, then the net force on the horse can be calculated as follows:
∑F = 30N − 20N = 10N
∑F = 10 N to the right
Application of the Second Law
The application of the second law of motion can be seen in identifying the amount of force needed to make an object move or to make it stop.
The following are a few examples that we have listed to help you understand this point:
- Kicking a ball
When we kick a ball, we exert force in a specific direction, which is the direction in which it will travel. In addition, the stronger the ball is kicked, the stronger the force we put on it and the further away it will travel. - Pushing a cart
It is easier to push an empty cart in a supermarket than it is to push a loaded one. More mass requires more force to accelerate. - Two people walking
Among the two people walking, if one is heavier than the other, then the one weighing heavier will walk slower because the acceleration of the person weighing lighter is greater.
Impulse
- Sometimes, we see situations where a really strong push happens quickly and changes an object's movement.
- For instance, when a ball hits a wall and bounces back, the force from the wall acts only for a short time, but it's powerful enough to make the ball go in the opposite direction.
- Figuring out the force and time separately can be tricky, but we can measure their combined effect, which is called impulse.
Impulse is the product of force and the time interval for which it acts. It equals the change in momentum of the object. Impulse (J) = F × Δt = m × Δv.
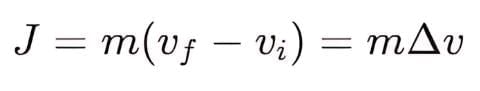 , where
, where
- Impulse-Momentum Theorem: J=FΔt, where
F: Average net force (N)
Δt: Time duration of force (s).
This states that impulse equals the change in momentum (J=Δp).
Derivation:
From Newton's Second Law (F=ma) and acceleration definition
- When a strong force acts for a short time to create a noticeable change in momentum, it's called an impulsive force. In science, impulsive forces used to be considered different from regular forces, but Newtonian mechanics doesn't make that distinction. Impulsive force is essentially like any other force, just stronger and quicker.
Newton’s Second Law Solved Examples
Example 1: If there is a block of mass 2kg, and a force of 20 N is acting on it in the positive x-direction, and a force of 30 N in the negative x-direction, then what would be its acceleration?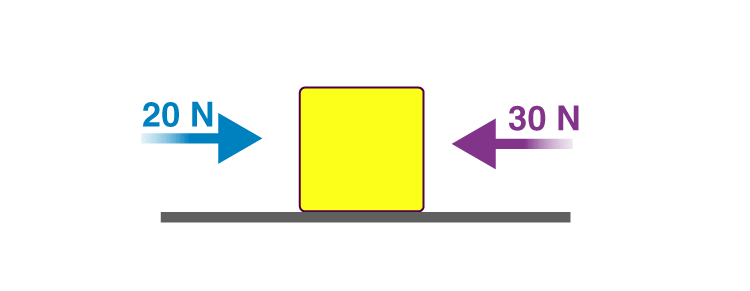 Solution: To calculate its acceleration, we first have to calculate the net force acting on it.
Solution: To calculate its acceleration, we first have to calculate the net force acting on it.
Fnet = 20 N – 30 N = -10 N
Mass = 2kg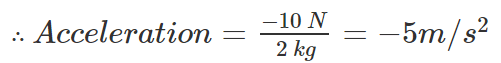
The negative acceleration indicates that the block is slowing and its acceleration vector is moving in an opposite direction directed opposite to the direction of motion.
Example 2: How much horizontal net force is required to accelerate a 1000 kg car at 4 m/s2?
Solution: Newton’s 2nd Law relates an object’s mass, the net force on it, and its acceleration. Therefore, we can find the force as follows:
Fnet = ma
Substituting the values, we get
1000 kg × 4 m/s2 = 4000 N
Therefore, the horizontal net force required to accelerate a 1000 kg car at 4 m/s2 is 4000 N.
Newton’s second law is applied in daily life to a great extent. For instance, in Formula One racing, the engineers try to keep the mass of cars as low as possible. Low mass will imply more acceleration, and the more the acceleration, the chances to win the race are higher.
What is Newton’s Third Law Of Motion?
When we press a spring, the spring is compressed by the force of our hand. In turn, the spring also exerts a force on our hand and we can feel it. Again, the earth pulls a stone downwards due to gravity. According to Newton, the stone exerts an equal and opposite force on the earth.
Newton’s third law states that “If one object exerts a force on another object, then the other object exerts an equal and opposite force on the first object”.
- An example of Newton’s third law is a book lying on a table, as shown in the image below. The book applies a force on the table, which is the book’s weight. In order to prevent deformation, the table exerts an equal and opposite force on the book. This force is the normal force.
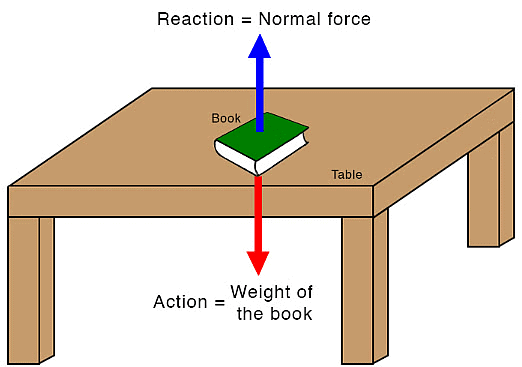 Newton's Third Law
Newton's Third Law
- Force is a push or pull acting on an object resulting in its interaction with another object. Force is a result of an interaction. Force can be classified into two categories: contact force such as frictional force and non-contact force such as gravitational force.
- Action Reaction Pairs: According to Newton, when two bodies interact, they exert force on each other, and these forces are known as action and reaction pairs, which is explained in Newton’s third law of motion.
- Newton’s third law of motion states that: “When one body exerts a force on the other body, the first body experiences a force which is equal in magnitude in the opposite direction of the force which is exerted”.
The above statement means that in every interaction, there is a pair of forces acting on the interacting objects. The magnitude of the forces are equal and the direction of the force on the first object is opposite to the direction of the force on the second object.
 Illustrations of Newton's third law of motion
Illustrations of Newton's third law of motion
Newton’s Third Law Equation
Suppose an object A exerts a force FAB on object B, and the latter exerts a force FBA on the former. Then, Newton’s third law can be written as,
FAB = – FBA
In other words, Action = – Reaction
Application in Aerodynamics: Rocket Propulsion
- The motion of a jet engine/rocket produces thrust hot exhaust gases flow out the back of the engine, and a thrusting force is produced in the opposite direction.
- Thrust is the power that propels an aircraft in the air, and it originates from the aircraft's propulsion system.
- Various propulsion systems create thrust using various methods, yet they all adhere to Newton's third law of motion, which states that for every action, there is an equal and opposite reaction.
- In any propulsion system, a working fluid gets accelerated by the system, and this acceleration leads to a force acting on the system. A fundamental derivation of the thrust equation illustrates that the thrust generated relies on both the mass flow passing through the engine and the velocity at which the gas exits the system.
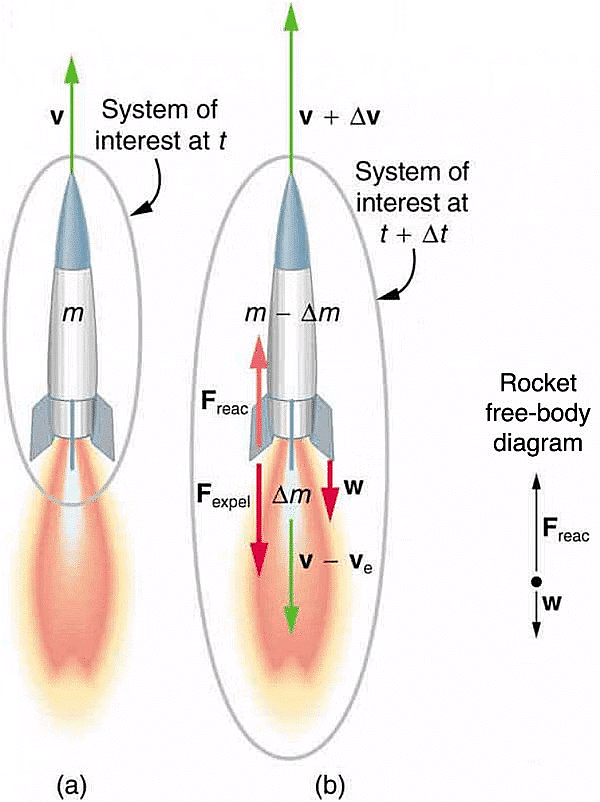 Illustration of Rocket Propulsion
Illustration of Rocket Propulsion
- Figure (a) shows the rocket has a mass of m and an upward velocity of v. The net external force on the system is −mg if air resistance is neglected.
- Figure (b) shows that a time Δt later the system has two main parts, the ejected gas and the remainder of the rocket. The reaction force on the rocket is what overcomes the gravitational force and accelerates it upward.
- Acceleration of a rocket is:
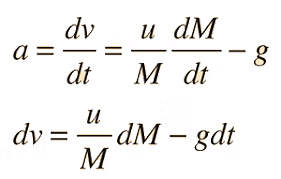 where a is the acceleration of the rocket, u is the exhaust velocity, M is the mass of the rocket, dM is the mass of the ejected gas, and dt is the time in which the gas is ejected.
where a is the acceleration of the rocket, u is the exhaust velocity, M is the mass of the rocket, dM is the mass of the ejected gas, and dt is the time in which the gas is ejected.
- The greater the exhaust velocity ve of the gases relative to the rocket, the greater the acceleration.
- The faster the rocket burns its fuel, the greater its acceleration.
- The smaller the rocket’s mass (all other factors being the same), the greater the acceleration.
Example 3: For rocket propulsion, the velocity of exhaust gases relative to the rocket is 2 km/s. If the mass of the rocket is 1000 kg. What is the rate of fuel consumption for a rocket to rise up with an acceleration of 4.9 m/s2?
Solution: Given:
- Velocity of exhaust gases, ve= 2 km/s = 2000 m/s
- Mass of rocket, m = 1000 kg
- Required acceleration, a = 4.9 m/s2
- Acceleration due to gravity, g = 9.8 m/s2
To find: Rate of fuel consumption (dm/dt)
The total thrust required is: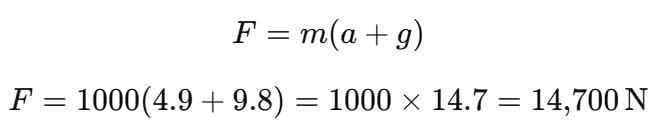
This thrust is provided by the exhaust gases:
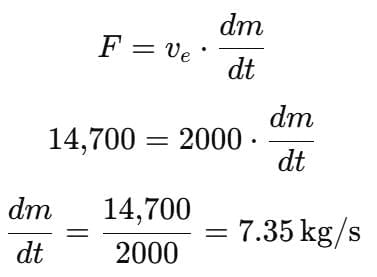
The rate of fuel consumption is 7.35 kg/s.
Example 4: Aswini and Deepa are standing on identical skateboards. Aswini and Deepa push off of each other and travel in opposite directions. If Aswini (M) and Deepa (m) have identical masses, who travels farther?
Solution: By the law of conservation of momentum, the total momentum before and after the push must be zero.
Let their velocities after the push be:
Aswini: vA
Deepa: vD
Since both have the same mass: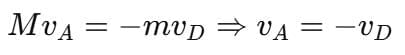
So, both have equal speed but in opposite directions.
If there is no friction, and they push off with equal and opposite forces (action–reaction), then they will move with equal speeds.
Hence, over the same amount of time, they will travel equal distances.
Examples of Interaction Force Pairs
A variety of action-reaction pairs are evident in nature. We have listed a few below, and they are as follows:
- Propulsion of Fish through Water: The propulsion of fish through water is an example of an action-reaction pair. A fish makes use of its fins to push water backward. This push serves to accelerate the fish forward. The size of the force on the water equals the size of the force on the fish; the direction of the force on the water (backward) is opposite the direction of the force on the fish (forward).
 Propulsion of Fish
Propulsion of Fish
- Flight of the Bird: The flight of the bird is an example of an action-reaction pair. The wings of the bird push the air downwards. The air pushes the bird upwards.
 Flight of the Bird
Flight of the Bird - Swimmer: A swimmer pushes against the water, while the water pushes back on the swimmer.
 Swimming
Swimming
Important Questions for Exam
Q1: While driving down the road, a firefly strikes the windshield of a bus and makes a quite obvious mess in front of the face of the driver. This is a clear case of Newton's third law of motion. The firefly hits the bus and the bus hits the firefly. Which of the two forces is greater: the force on the firefly or the force on the bus?
Answer: Each force is the same size. For every action, there is an equal reaction. The fact that the firefly splatters only means that with its smaller mass, it is less able to withstand the larger acceleration resulting from the interaction.
Q2: Many people are familiar with the fact that a rifle recoils when fired. This recoil is the result of action-reaction force pairs. A gunpowder explosion creates hot gases that expand outward allowing the rifle to push forward on the bullet. Consistent with Newton's third law of motion, the bullet pushes backward upon the rifle. The acceleration of the recoiling rifle is____________ (greater/ smaller/ same) as the acceleration of the bullet.
Answer: The force on the rifle equals the force on the bullet. Yet, acceleration depends on both force and mass. The bullet has a greater acceleration due to the fact that it has a smaller mass. Remember: acceleration and mass are inversely proportional.
Q3: The forces involved in Newton’s third law act ____
a) On the same object
b) On different objects
c) In same direction
d) On five bodies
Answer: b
Explanation: The two forces involved in Newton’s third law are the cause force and the reaction force. The cause force acts on the contact surface or the contact body by the parent body. Whereas the reaction force acts on the parent body by the contact body.
Q4: A batsman hits a ball with a force a 5 N. What force does the bat experience?
a) 5 N
b) 10 N
c) 15 N
d) 20 N
Answer: a
Explanation: From Newton’s third law we know that for every action, there is an equal and opposite reaction. From this we can say that the bat experiences a force of 5 N.
Q5: A truck with a mass of 2500 Kg travelling with an acceleration of 5 m/s2 hits a scooter. What force does the truck experience?
a) 12500 N
b) 500 N
c) 10000 N
d) 2500 N
Answer: a
Explanation: According to Newton’s third law, the ball exerts a force of 5 N on the bat, and the bat experiences an equal and opposite force of 5 N from the ball.
|
119 videos|491 docs|98 tests
|
FAQs on Newton's Laws of Motion - Physics Class 11 - NEET
| 1. What is the First Law of Motion? |  |
| 2. What is an External Force? |  |
| 3. What is Newton’s Second Law of Motion? |  |
| 4. What is a Net Force? |  |
| 5. What are Applications of Inertia? |  |