Laws of Motion & their Application | Science for Grade 8 PDF Download

Newton's Laws of Motion

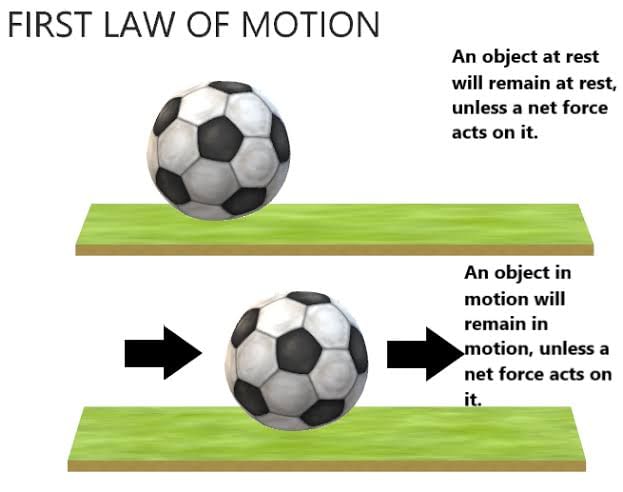
Newton’s First Law of Motion

A body at rest will remain at rest, and a body in motion will continue in motion in straight line with a uniform speed, unless it is compelled by an external force to change its state of rest or of uniform motion.

The tendency of a motionless body to remain at rest, or if moving, to continue moving in a straight line, is called inertia.

Key Point : Mass is measure of the inertia of a body. Heavier objects have more inertia and require more force to move as compared to the lighter objects.

The force required to stop a moving body is directly proportional to the mass and velocity of that body.

Example :

Key Note : Every moving body possesses momentum.

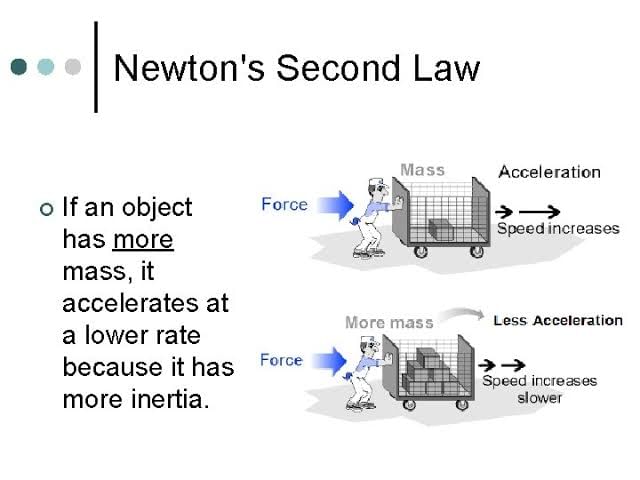
Newton's Second Law of Motion

According to Newton’s second law of motion, the rate of change of momentum of a body is directly proportional to the applied force, and takes place in the direction in which the force acts.

The force necessary to change the momentum of an object depends on the time taken at which the

momentum is changed.

Force ∝ Change in momentum/ Time taken

or F ∝ mv-mu/t

or F ∝ m(v-u)/t

      F ∝ ma

Thus the force acting on a body is directly proportional to the product of ‘mass’ of the body and the 'acceleration’ produced in the body by the action of the force, and it acts in the direction of acceleration.

F = k × m × a

In SI units, value of constant k is 1. So the equation becomes

F = ma

Putting m = 1 kg and a = 1 m/s², F becomes 1 Newton. 

Key Note : A Newton is that force which when acting on a body of mass 1 kg produces on acceleration of 1 m/s² in it, represented by 1N.

Applications of Newton’s second law :

• A cricket fielder moves his hands backwards on catching a fast running cricket ball, in order to increase the time taken to reduce the momentum of ball to zero.
• A high jumping athlete is provided either a cushion or a heap of sand on the ground to fall upon. This cushion or sand, being soft reduces the athlete’s momentum more gently.

Newton’s Third Law of Motion

Newton’s third law of motion describes the relationship between the forces that come into play when the two bodies interact with one another. According to this law,

Whenever one body exerts a force on another body, the second body exerts an equal and opposite force on the first body. It can also be written as ‘ To every action, there is an equal and opposite reaction.’

Key Note : Action and reaction are just forces acting on two different bodies, and they act simultaneously.

Application of third law :

• The box exerts ‘action’ ( force of its weight ) in downward direction on the ground. The ground is exerting an equal and opposite force, upward, on the box, which we called ‘reaction’.
• Same way, when a gun is fired, it exerts a forward force on the bullet. The bullet exerts an equal and opposite reaction force on the gun which makes the gun recoil back.
• In another case, as the sailor jumps from the boat in forward direction towards the shore, the boat moves backward in water.

All these examples prove the Newton's third law of motion. 

Conservation of momentum

According to the law of conservation of momentum, 

'when two (or more )bodies collide with one another, their total momentum remains constant (or conserved) provided no external forces are acting.’

It means that whenever one body gains momentum, then the other body must lose an equal amount of momentum so that total momentum of the two bodies remains same. Thus, the law states that 'Momentum is neither created nor destroyed.’ 

Suppose two bodies, a truck (of mass m₁ and speed u₁) and a car (of mass m₂ and speed u₂) are moving in the same direction. Then,

After collision, they again move in the same direction but with new velocities, m₁ with v₁  and m₂ with v₂ due to forces acting on each other.

Momentum after collision = m₁v₁ + m₂v₂

According to this law,

Total momentum before collision = Total momentum after collision

m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

Applications of the law of conservation of momentum 

• The chemicals inside the rocket burn and produce high velocity blast of hot gases passing through the tail nozzle of the rocket in the downward direction. The rocket moves up to balance the momentum of gases.

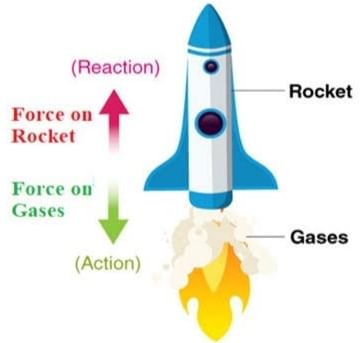
 Although the mass of gases emitted is comparatively small, but they have a very high velocity and hence a very large momentum. An equal momentum is imparted to the rocket in the opposite direction, so that, in spite of its large mass, the rocket goes up with a high velocity.