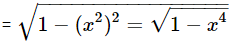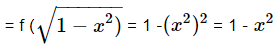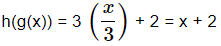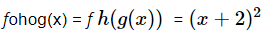Inverse Functions & Composition of Functions | Engineering Mathematics - Engineering Mathematics PDF Download

Introduction

A composite function is usually composed of other functions such that the output of one function is the input of the other function. In other words, when the value of a function is found from two other given functions by applying one function to an independent variable and the other to the result of the other function whose domain consists of those values of the independent variable for which the result yielded by the first function lies in the domain of the second.
Example: Two functions - 3y+5 and y² together forms a composite function which can be written as (3y+5)²

Explanation of Composition Functions

To form a composite function by a composition of two other functions we need to take two functions say g(x) = x² and f(x) = x+5. Now, we need to put one function inside the other function so here we can put f(x) into g(x) to form a new function, called their composition.
As mentioned above, to form composite functions we need to insert one function into another. Here f(x) can be plugged into g(x) to form a function g(f(x)). We know that f(x) = x + 5, thus we can substitute the function in. Therefore, g(f(x)) = g(x + 5). Knowing the fact that g(x) = x²
 we can insert the function and evaluate g(x + 5) = (x+5)². Therefore, g(f(x)) = g(x + 5) = (x+5)² .
For practice, download composition of functions examples with answers pdf. By downloading composition of functions examples with answers pdf, you will have enough composite functions questions for practising. 

Composite Functions Properties

There are four major properties of a composite function:

Property 1:  Composite functions are not commutative
gof is not equal to fog

Property 2: Composite functions are associative
(fog)oh = fo(goh)

Property 3:  A function f: A -B and g: B-C is one-one then gof: A-C is also one-one.

Property 4: A function f: A-B and g: B-C is onto then gof: A-C is also onto.

What is Inverse Function? 
An inverse function is a function, which can reverse into another function. In other words, if any function “f” takes p to q then, the inverse of “f” i.e. “f-1” will take q to p.  A function accepts a value followed by performing particular operations on these values to generate an output. If you consider functions, f and g are inverse, then f(g(x)) is equal to g(f(x)) which is equal to x. 

Given below are the detailed summary of the Composition and inverse relation with examples:
Composite and Inverse Functions

 Example 1: Let f(x) = x² and 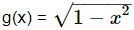 Find (gof)(x) and (fog)(x).

(gof)(x) = g(f(x)) = g(x²)
(fog) (x) = f(g(x))

Example 2:  If f(x) =x² , g(x) =x/3 and h(x) = 3x+2 . Find out fohog(x)

Therefore this is the required solution.