Introduction to Lines & Angles | The Complete SAT Course - Class 10 PDF Download
Line
A line does not have any endpoints. It has an infinite length.

Line Segment
A Line segment is a segment of a line, or in other words, we can say that a line segment is a line with two endpoints.
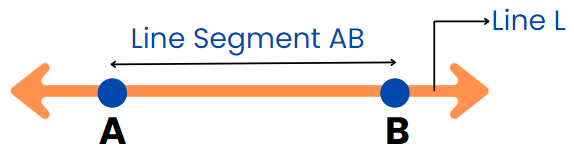
 The diagram shows a line L and one segment of this line is AB. In a plane, there can be many lines or line segments
The diagram shows a line L and one segment of this line is AB. In a plane, there can be many lines or line segments- These lines can be divided into a few types based on the relative positioning of a line with another line.
Intersecting Lines
Two lines are intersecting lines if they meet each other at a common point.
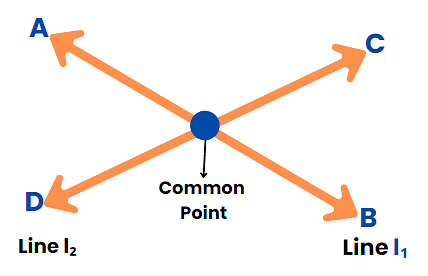
Example, l1 and l2 are intersecting lines in the diagram
Parallel Lines
A Pair of lines are Parallel if they never intersect.
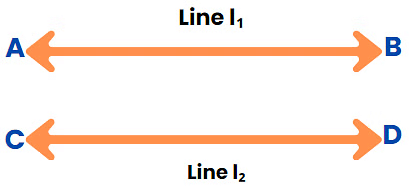
Example, L1, L2, and L3 are parallel lines in the diagram.
Transversal Line
A Transversal line cuts two or more lines at distinct points.
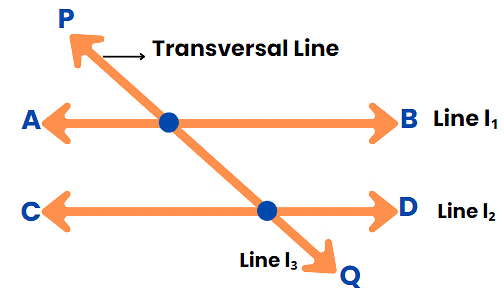
Example, Line L3 is the transversal line in the diagram.
Angle
An Angle is formed when two lines intersect each other. We represent an angle by the symbol ∠.
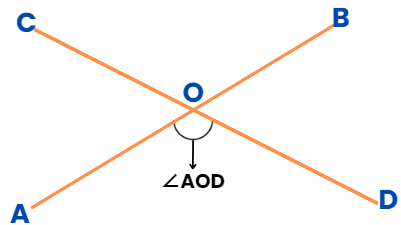
- An angle involves two legs and one common vertex at which two lines meet.
- For example, ∠AOD is formed when lines AB and CD intersect with each other.
- Also, ∠AOD is formed between the leg AO and OD, so we include A, O, and D while naming the angle.
Measurement of an Angle
The Angle is measured in degrees.
An angle can measure from zero (0) degrees to 360 degrees. 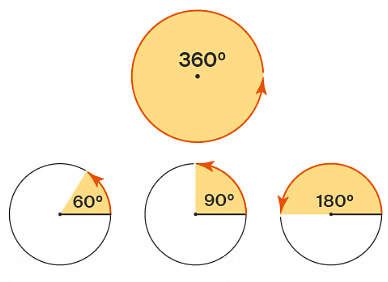 Based on the measurement of an angle, they are divided into four types:
Based on the measurement of an angle, they are divided into four types:
- Acute angle
- Right angle
- Obtuse angle
- Reflex angle
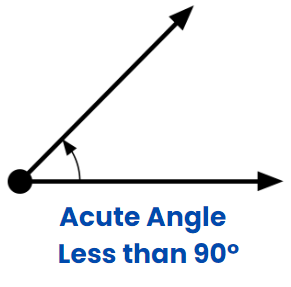
Acute Angle
When the measurement of the angle is between 0 degrees and 90 degrees.
Right Angle
When the measurement of the angle is exactly 90 degree.
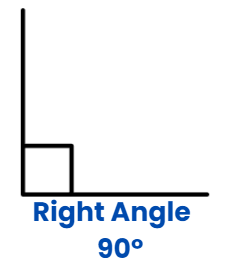
If there is a right angle between two lines, then the two lines are said to be perpendicular to each other.
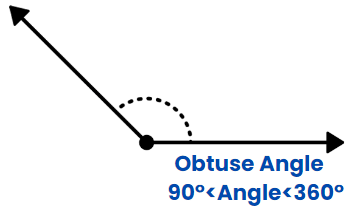
Obtuse Angle
When the measurement of the angle is between 90 degrees and 180 degrees.
Straight Angle
A straight line has an angle of 180 degrees.

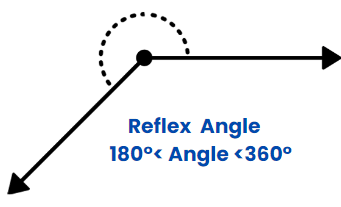
Reflex Angle
When the measurement of the angle is between 180 degrees and 360 degrees.
Angles formed between two intersecting lines
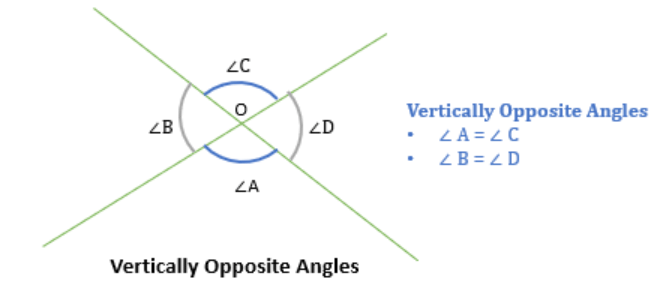
Vertically Opposite Angles
- When two lines intersect with each other, then 4 angles are formed.
- The angles that are opposite to each other at the intersection point are known as vertically opposite angles.
- Vertically opposite angles are always equal.
Let us now discuss the angles formed when two lines are intersected by a third line i.e. a transversal line.
Angles formed by a transversal line
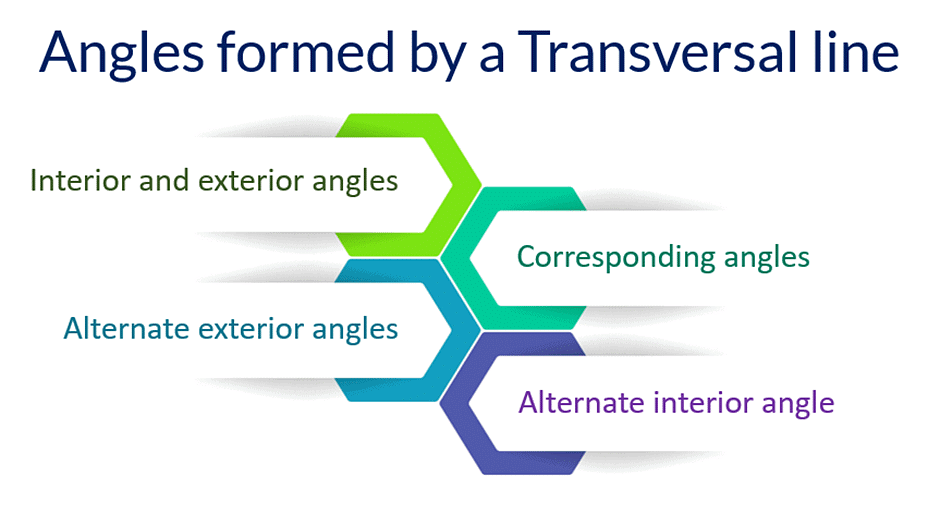
- When a transversal line intersects two lines, then eight angles are formed as shown.
- Now, there are several special pairs of angles that are obtained from this diagram.
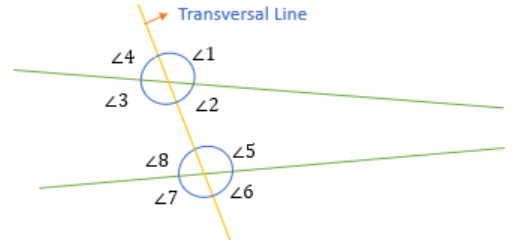
- For Example: If you notice (∠1, ∠3), (∠2, ∠4), (∠5, ∠7), and (∠6, ∠8) are all vertically opposite angles.
- Similarly, we get several other types of angles. Let us discuss them.
Other types of Angles
Interior and Exterior Angles
- Interior angles are the ones that are present inside the region between two lines.
Exterior angles are the ones that are not present inside this region.
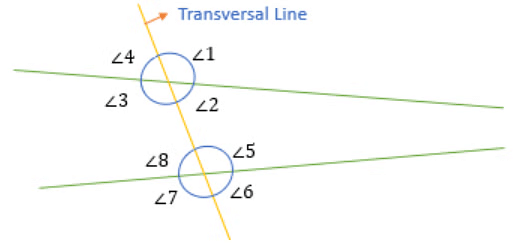
For example:
- ∠2, ∠3, ∠5, and ∠8 are Interior angles.
- And, ∠1, ∠4, ∠6, and ∠7 are Exterior angles.
Corresponding Angles
Two angles are said to be corresponding angles if they lie on the same side of the transversal line such that:
- One angle is an interior angle,
- Another is an exterior angle
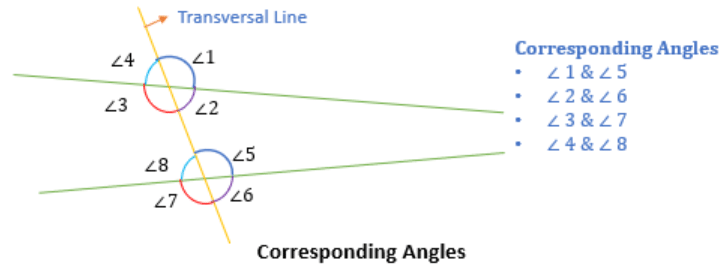
For Example:
(∠4, ∠8), (∠3, ∠7), (∠1, ∠5), and (∠2, ∠6) are 4 pairs of corresponding angles
Alternate interior angles
Two interior angles, present on the opposite side of a transversal line, are called alternate interior angles.
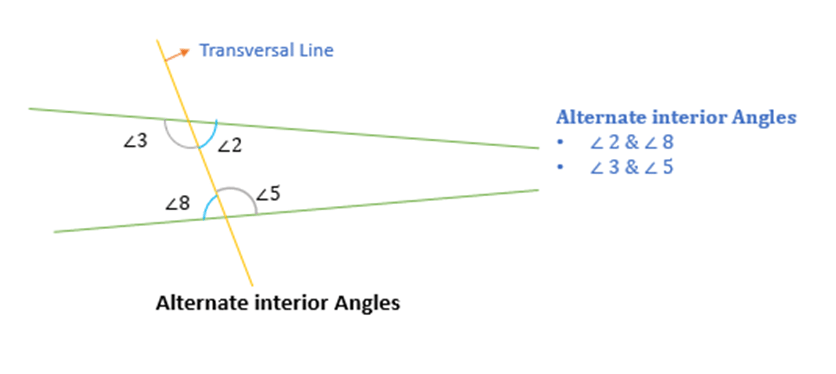 For example:
For example:
(∠2, ∠8) and (∠3, ∠5) are alternate interior angles.
Alternate exterior angles
Two exterior angles that are present on the opposite side of the transversal line are called alternate exterior angles.
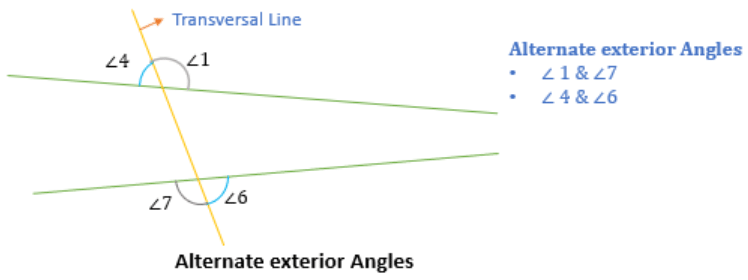
For example:
(∠1, ∠7) and (∠4, ∠6) are alternate exterior angles.
Note: If a transversal line intersects two parallel lines, then the corresponding angles, alternate interior angles, and alternate exterior angles are equal.
Properties of Angles
Sum of angles on one side of a straight line
The sum of all the angles on one side of a straight line is always 180 degrees.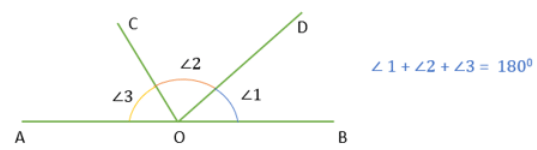
For Example, The sum of ∠1, ∠2, and ∠3 is 180 degrees.
Sum of angles around a point
The sum of all the angles around a point is always 360 degrees.
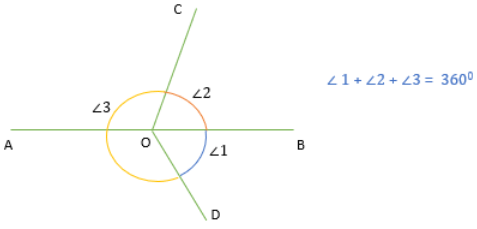
For example, Sum of angles (∠1, ∠2, and ∠3) around point O is 360 degrees.
|
433 videos|220 docs|166 tests
|
FAQs on Introduction to Lines & Angles - The Complete SAT Course - Class 10
| 1. What is a line in geometry? |  |
| 2. How are lines and angles related in geometry? |  |
| 3. What are the different types of angles formed by intersecting lines? |  |
| 4. What is the significance of parallel and perpendicular lines in angles? |  |
| 5. How can I calculate the measure of an angle formed by two intersecting lines? |  |
















