Introduction & Solving Quadratic Equations | Mathematics (Maths) Class 10 PDF Download
Quadratic Equations appear in many aspects of our daily lives. For instance, even designing a playground can be expressed as a quadratic equation. Because many situations lead to quadratic equations, there is a real interest in finding their solutions. A quadratic equation in the variable x takes the form ax² bx c = 0, where a, b, and c are real numbers, and a ≠ 0. The solutions to a quadratic equation are the points where the equation holds true, meaning Q(x) = 0. These solutions are also referred to as the roots or zeros of the quadratic equation. Various real-life applications of quadratic equations will be explored. Below are some methods for solving quadratic equations.
Quadratic Equation
A quadratic equation is a second-degree polynomial. Its general form is given by,
ax2 + bx + c = 0
a, b and c are real numbers while a ≠ 0. Its shape is a parabola that opens upwards or downwards depending upon the value of “a”.
Its solution is the point where the equation is satisfied. There are several methods of finding out a solution to the quadratic equation given as follows:
- Factoring
- Quadratic Formula
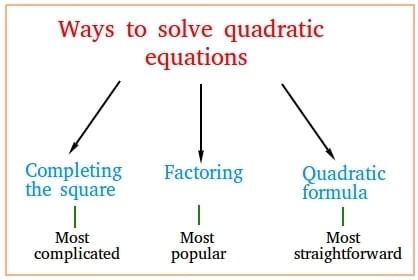 Methods to solve quadratic equations
Methods to solve quadratic equations
Factoring
We try to factor out the equation such that we get the equation in form of the product of two terms. Then on equating these two terms to zero, we get the roots.
To find the roots using factorisation, follow these steps:
- All the terms must be on one side of the equation, either LHS or RHS leaving zero on the other side.
- Factorize the equation
- Set the factors equal to zero to find the roots one by one.
Let’s look at this method in more detail using the examples below:
Question 1: Factorize the following equation and find its roots: 2x2 – x – 1 = 0
Solution:
2x2 – x – 1 = 0
⇒ 2x2 -2x + x – 1 = 0
⇒ 2x(x – 1) + 1(x – 1) = 0
⇒ (2x + 1) (x – 1) = 0
For this equation two be zero, either one of these or both of these terms should be zero.
So, we can find out roots by equating these terms with zero.
2x + 1 = 0
x = -1/2
x – 1 = 0
⇒ x = 1
So, we get two roots in the equation.
x = 1 and -1/2
Question 2: Factorize the following equation and find its roots: x2 + x – 12 = 0
Solution:
x2 + x – 12 = 0
⇒ x2 + 4x – 3x – 12 = 0
⇒ x(x + 4) -3(x + 4) = 0
⇒ (x – 3) (x + 4) = 0
Equating both of these terms with zero.
x – 3 = 0 and x – 4 = 0
x = 3 and 4
Quadratic Formula
All the quadratic equations can be solved using the quadratic formula.
For an equation of the form,
ax2 + bx + c = 0,
Where a, b and c are real numbers and a ≠ 0.
The roots of this equation are given by,
x = 
Given that b2 – 4ac is greater than or equal to zero.
Question 1: Find out the roots of the equation using Quadratic Formula,
Solution:
4x2 + 10x + 3 = 0
Using Quadratic Formula to solve this,
a = 4, b = 10 and c = 3
Before plugging in the values, we need to check for the discriminator
b2 – 4ac
⇒ 102 – 4(4)(3)
⇒ 100 – 48
⇒ 52
This is greater than zero, So now we can apply the quadratic formula.
Plugging the values into quadratic equation,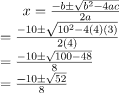
Question 2: Find out the roots of the equation using Quadratic formula,
5x2 + 9x + 4 = 0
Solution:
5x2 + 9x + 4 = 0
Using Quadratic Formula,
a = 5, b = 9 and c = 4.
Before plugging in the values, we need to check for the discriminator
b2 – 4ac
⇒ 92 – 4(5)(4)
⇒ 81 – 80
⇒ 1
This is greater than zero, So the quadratic formula can be applied. Plugging in the values in the formula,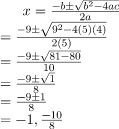
|
127 videos|655 docs|84 tests
|
FAQs on Introduction & Solving Quadratic Equations - Mathematics (Maths) Class 10
| 1. What is a quadratic equation and how is it defined? |  |
| 2. How can I solve a quadratic equation using the quadratic formula? |  |
| 3. What are the different methods to solve quadratic equations? |  |
| 4. What does the discriminant of a quadratic equation indicate? |  |
| 5. Can all quadratic equations be solved by factoring? |  |






















