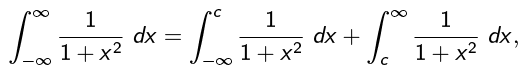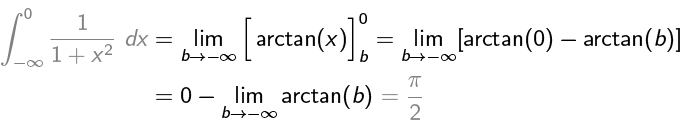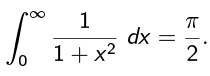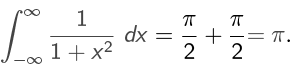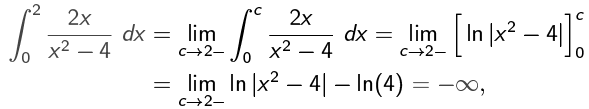Improper Integrals | Engineering Mathematics - Engineering Mathematics PDF Download
Definite integrals 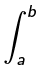 f (x) dx were required to have
f (x) dx were required to have
- finite domain of integration [a, b]
- finite integrand f (x ) < ±∞
Improper integrals
- Infinite limits of integration
- Integrals with vertical asymptotes i.e. with infinite discontinuity
Improper integrals are said to be
- convergent if the limit is finite and that limit is the value of the improper integral.
- divergent if the limit does not exist.
Each integral on the previous page is defined as a limit.
If the limit is finite we say the integral converges, while if the limit is infinite or does not exist, we say the integral diverges.
Convergence is good (means we can do the integral); divergence is bad (means we can’t do the integral).
Example 1: Find 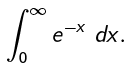
(if it even converges)
So the integral converges and equals 1.
Example 2: Find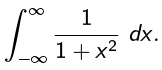
(if it even converges)
By definition,
where we get to pick whatever c we want. Let’s pick c = 0.
Similarly,
Therefore,
Example 3: the p-test
The integral
Converges if p > 1;
Diverges if p ≤ 1.
For example: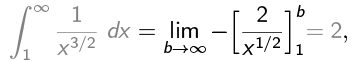
while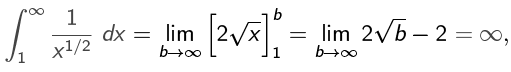
and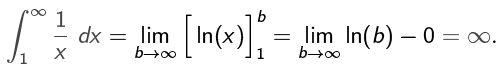
Convergence vs. Divergence
- In each case, if the limit exists (or if both limits exist, in case 3!), we say the improper integral converges.
- If the limit fails to exist or is infinite, the integral diverges. In case 3, if either limit fails to exist or is infinite, the integral diverges.
Example 4: Find 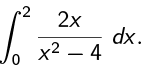
(if it converges)
The denominator of 2x/x2 - 4 is 0 when x = 2, so the function is not even defined when x = 2. So
so the integral diverges.
Example 5: Find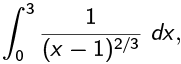 if it converges.
if it converges.
We might think just to do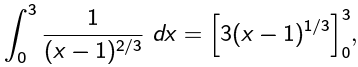
but this is not okay: The function 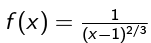 is undefined when x = 1, so we need to split the problem into two integrals.
is undefined when x = 1, so we need to split the problem into two integrals.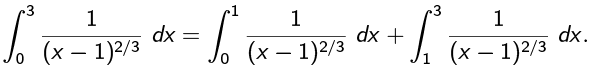
The two integrals on the right hand side both converge and add up to 3[1 + 21/3],
so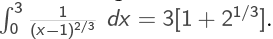
|
65 videos|133 docs|94 tests
|