Open App

Class 8 Exam > Class 8 Notes > Mathematics (Maths) Class 8 > Important Questions: Mensuration

Important Questions for Class 8 Maths - Mensuration

Table of contents
Match the column
Fill in the blanks
True & False
Answer the following questions

Match the column

Q1:

Ans:
(p) → (iv)
(q) → (i)
(r) → (ii)
(s) → (iii)

Sol : Important Questions for Class 8 Maths - Mensuration

Q2:

Ans:

(p) → (ii)

(q) → (iii)

(r) → (i)

Sol:

Fill in the blanks

(i) Curved surface area of a cylinder of radius 2b and height 2a is _______.
(ii) Volume of a cylinder with radius p and height q is __________.
(iii) 6.55m²= ______cm²
(iv)The volume of a cylinder becomes __________ the original volume if its radius becomes doubles of the original radius and height becomes half of its original values
Ans:

(i) $S = 2 π r H = 2 π 2 b 2 a = 8 π a b$

$S = 2 π r H = 2 π 2 b 2 a = 8 π a b$
$S = 2 π r H = 2 π 2 b 2 a = 8 π a b$
$S = 2 π r H = 2 π 2 b 2 a = 8 π a b$

(ii) $V = π r^{2} H = π p^{2} q$

$V = π r^{2} H = π p^{2} q$
$V = π r^{2} H = π p^{2} q$
$V = π r^{2} H = π p^{2} q$
$V = π r^{2} H = π p^{2} q$

(iii) 65,500cm²
$V = π r^{2} H = π p^{2} q$ $V = π r^{2} H = π p^{2} q$
6.55m²= 6.55×10,000cm²= 65,500cm²

(iv)double
$V = π r^{2} H = π p^{2} q$ $V_{1} = π r^{2} H$ ,
$V_{2} = π (2 r)^{2} (1 / 2) H = 2 p i r^{2} H$
$V_{2} = π (2 r)^{2} (1 / 2) H = 2 p i r^{2} H$ ,
So it becomes double

True & False

(i) Amount of region occupied by a solid is called its surface area
(ii)The areas of any two faces of a cube are equal.
(iii)The areas of two oppossite faces of a cuboid are equal.
(iv) 2.5 litres is equal to 0.025 cubic meters
(v) Total surface area of cuboid is 2h (l + b).
Ans:
(i)False
Sol: The amount of region occupied by a solid is called its volume, not surface area.
(ii)True
Sol: All six faces of a cube are squares and have equal areas.
(iii) True
Sol: Opposite faces of a cuboid are identical in dimensions, hence their areas are equal.
(iv) False
Sol: 1litre = 0.001m³, so

2.5 \, \text{litres} = 2.5 \times 0.001 = 0.0025 \, \text{m}^3

2.5litres = 2.5 × 0.001 = 0.0025m³. (This makes it True, correcting the prior explanation.)
(v) False
Sol: Total surface area of cuboid = 2(lb + bh + hl), not 2h (l + b).

Answer the following questions

Q1: The parallel sides of a trapezium are 20 cm and 10 cm. Its nonparallel sides are both equal, each being 13 cm. Find the area of the trapezium.
Sol:Let ABCD is the trapezium with AB and CD are the parallel sides.
Now
AB=10 cm, CD=20 cm, BC=13 cm
Now draw line BE || AD and draw a perpendicular from B on EC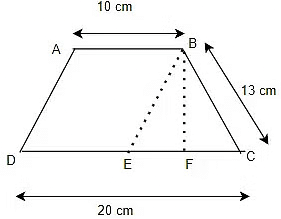
Important Questions for Class 8 Maths - Mensuration Now ABED is a parallelogram, then BE=13 cm
In triangle BEC, BE =BC, So Isoceles triangle,So perpendicular will bisect the EC
Hence EF = FC
Now EC= DC -DE = 20 -10 =10 cm
Therefore EF = FC = EC/2 = 5 cm
Now in Triangle BEF, it is right angle at F,So by pythagorous theorem
$B E^{2} = B F^{2} + E F^{2}$
$169 = B F^{2} + 25$
$B F = 12 c m$
This is also the perpendicular distance between the parallel sides. So now coming back to Area of trapezium
$A = \frac{1}{2} [a + b] \times h$
Here a = 10 cm , b = 20 cm, h = 12 cm., A =?
Therefore
$A = \frac{1}{2} [10 + 20] \times 12$
$A = 180 c m^{2}$

Q2: The area of a rhombus is 300 cm², and one of the diagonals is 20 cm. Find the other diagonal.

$A = 180 c m^{2}$
Important Questions for Class 8 Maths - Mensuration Q3: A circular garden has a radius of 14 m. Find the cost of fencing the garden along its circumference at the rate of ₹12 per meter.
Sol:
$h = 38$
$h = 38$ $h = 38$
$h = 38$
$h = 38$
$h = 38$
$h = 38$
$h = 38$

$h = 38$
$h = 38$
$h = 38$
$h = 38$
$h = 38$
$h = 38$
$h = 38$
$h = 38$

$h = 38$
$h = 38$
Important Questions for Class 8 Maths - Mensuration $h = 38$
Sol:
Area of trapezium=Half the product of the sum of the lengths of parallel sides and the perpendicular distance between them gives the
$A = \frac{1}{2} [a + b] \times h$
Here a = 2x cm , b = 6x, h = 12 cm., A = 384 cm²
Therefore
$384 = \frac{1}{2} [2 x + 6 x] \times 12$
$x = 8$ cm
So parallel sides are 16 cm and 48 cm

Q8: A cylindrical road roller makes 750 complete revolutions to level a road. The diameter of the roller is 84 cm, and its length is 1 m. Calculate the total area leveled by the road roller.
Sol:
Important Questions for Class 8 Maths - Mensuration
Q9: A rectangular piece of cardboard measuring 18 cm × 7 cm is folded without overlapping to make a cylinder of height 7 cm. Find the volume of the cylinder.

Sol:

Q10: A storage room is in the shape of a cuboid with dimensions 50 m × 30 m × 20 m. How many smaller cuboidal containers of volume 1.2 m³ can be stored in it?

Sol:
Important Questions for Class 8 Maths - Mensuration

The document Important Questions for Class 8 Maths - Mensuration is a part of the Class 8 Course Mathematics (Maths) Class 8.

All you need of Class 8 at this link: Class 8

	Mathematics (Maths) Class 8 81 videos\|452 docs\|31 tests

Mathematics (Maths) Class 8

81 videos|452 docs|31 tests

Join Course for Free

FAQs on Important Questions for Class 8 Maths - Mensuration

1. What is mensuration in mathematics?

Ans.Mensuration is a branch of mathematics that deals with the measurement of geometric figures and their parameters, such as length, area, and volume. It involves calculations related to two-dimensional and three-dimensional shapes, helping to determine sizes and capacities.

2. How do you calculate the area of a rectangle?

Ans.To calculate the area of a rectangle, you multiply its length by its width. The formula is: Area = Length × Width. For example, if the length is 5 units and the width is 3 units, the area would be 5 × 3 = 15 square units.

3. What is the formula for finding the volume of a cylinder?

Ans.The volume of a cylinder can be calculated using the formula: Volume = π × r² × h, where "r" is the radius of the base and "h" is the height of the cylinder. For instance, if the radius is 2 units and the height is 5 units, the volume would be π × (2)² × 5 = 20π cubic units.

4. What is the difference between perimeter and area?

Ans.Perimeter refers to the total distance around a two-dimensional shape, while area measures the extent of the space contained within that shape. For example, a rectangle has a perimeter calculated by adding up all its sides, while the area is found by multiplying its length and width.

5. How can I find the surface area of a cube?

Ans.The surface area of a cube can be found using the formula: Surface Area = 6 × a², where "a" is the length of one side of the cube. For example, if each side measures 4 units, the surface area would be 6 × (4)² = 96 square units.

About this Document

4.9K Views

4.91/5 Rating

Sep 11, 2025 Last updated

Related Exams

Class 8 CTET & State TET JSS 2 Grade 8 EMRS Bihar PGT/TGT/PRT Jharkhand (JSSC) PRT/TGT KVS PGT/TGT/PRT NVS TGT/PGT CG TET

Document Description: Important Questions: Mensuration for Class 8 2025 is part of Mathematics (Maths) Class 8 preparation. The notes and questions for Important Questions: Mensuration have been prepared according to the Class 8 exam syllabus. Information about Important Questions: Mensuration covers topics like Match the column, Fill in the blanks, True & False, Answer the following questions  and Important Questions: Mensuration Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Questions: Mensuration.

Introduction of Important Questions: Mensuration in English is available as part of our Mathematics (Maths) Class 8 for Class 8 & Important Questions: Mensuration in Hindi for Mathematics (Maths) Class 8 course. Download more important topics related with notes, lectures and mock test series for Class 8 Exam by signing up for free. Class 8: Important Questions for Class 8 Maths - Mensuration

Description

Full syllabus notes, lecture & questions for Important Questions for Class 8 Maths - Mensuration - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 8 | Best notes, free PDF download

Information about Important Questions: Mensuration

In this doc you can find the meaning of Important Questions: Mensuration defined & explained in the simplest way possible. Besides explaining types of Important Questions: Mensuration theory, EduRev gives you an ample number of questions to practice Important Questions: Mensuration tests, examples and also practice Class 8 tests

	Mathematics (Maths) Class 8 81 videos\|452 docs\|31 tests

Mathematics (Maths) Class 8

81 videos|452 docs|31 tests

Join Course for Free

Download as PDF

Explore Courses for Class 8 exam

MCQs

practice quizzes

Previous Year Questions with Solutions

shortcuts and tricks

Important Questions for Class 8 Maths - Mensuration

study material

Important questions

Free

Viva Questions

Extra Questions

mock tests for examination

Summary

Objective type Questions

ppt

Important Questions for Class 8 Maths - Mensuration

Exam

Semester Notes

past year papers

Sample Paper

video lectures

pdf

;

Additional Information about Important Questions: Mensuration for Class 8 Preparation

Important Questions: Mensuration Free PDF Download

The Important Questions: Mensuration is an invaluable resource that delves deep into the core of the Class 8 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Important Questions: Mensuration now and kickstart your journey towards success in the Class 8 exam.

Importance of Important Questions: Mensuration

The importance of Important Questions: Mensuration cannot be overstated, especially for Class 8 aspirants. This document holds the key to success in the Class 8 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Important Questions: Mensuration Notes

Important Questions: Mensuration Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Important Questions: Mensuration. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Important Questions: Mensuration Notes on EduRev are your ultimate resource for success.

Important Questions: Mensuration Class 8

The "Important Questions: Mensuration Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Important Questions: Mensuration on the App

Students of Class 8 can study Important Questions: Mensuration alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Important Questions: Mensuration, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Important Questions: Mensuration is prepared as per the latest Class 8 syllabus.

Education Revolution

Signup to see your scores go up
within 7 days!

Continue with Google

Takes less than 10 seconds to signup