Class 8 Exam > Class 8 Notes > Mathematics Class 8- New NCERT (Ganita Prakash) > Important Formula: Proportional Reasoning-1
Important Formula: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
| Table of contents |
|
| Proportional Change |
|
| Ratios |
|
| Proportion |
|
| Rule of Three (Trairasika) |
|
| Sharing in a Given Ratio |
|
| Unit Conversions |
|
Proportional Change
If width factor = height factor, shape remains similar.
If width factor ≠ height factor, shape becomes distorted.
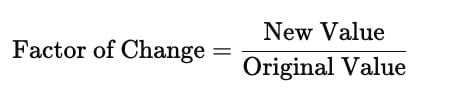
Ratios
- General form:
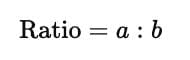
- Simplest form of ratio:
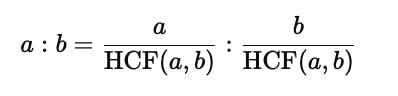
Proportion
Two ratios are proportional if:
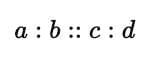
Condition:
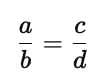or
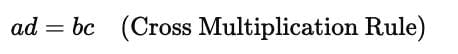
Rule of Three (Trairasika)
If three quantities are known and the fourth is to be found:
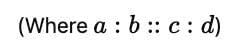
Sharing in a Given Ratio
To divide a quantity x in the ratio m:n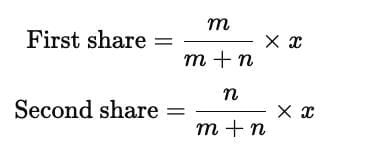
Unit Conversions
Length
1 metre = 3.281 feet
Area
1 square metre = 10.764 square feet
1 acre = 43,560 square feet
1 hectare = 10,000 square metres = 2.471 acres
Volume
1 millilitre = 1 cubic centimetre
1 litre = 1000 millilitres = 1000 cubic centimetres
Temperature
Fahrenheit = (9/5 × Celsius) + 32
Celsius = (5/9) × (Fahrenheit – 32)
The document Important Formula: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash) is a part of the Class 8 Course Mathematics Class 8- New NCERT (Ganita Prakash).
All you need of Class 8 at this link: Class 8
|
20 videos|139 docs|11 tests
|
FAQs on Important Formula: Proportional Reasoning-1 - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is proportional change, and how can it be calculated? |  |
Ans.Proportional change refers to the change in a quantity relative to its original value, often expressed as a percentage. To calculate proportional change, you can use the formula: Proportional Change = (New Value - Original Value) / Original Value × 100%. This gives you the percentage increase or decrease from the original value.
| 2. How do ratios work, and what are their practical applications? | |
Ans.Ratios are a way to compare two quantities by division, indicating how many times one value contains or is contained within the other. They are expressed in the form of a:b or a/b. Ratios are commonly used in various fields, including cooking (to mix ingredients), finance (to analyze investments), and statistics (to understand data relationships).
| 3. What is a proportion, and how is it different from a ratio? | |
Ans.A proportion is an equation that states that two ratios are equal. For example, if a/b = c/d, then a, b, c, and d are in proportion. The key difference is that a ratio compares two quantities, while a proportion asserts the equality of two ratios. Proportions are useful in solving problems involving scaling and comparisons.
| 4. What is the Rule of Three (Trairasika), and when is it used? | |
Ans.The Rule of Three, or Trairasika, is a mathematical principle used to find a fourth value when three values are known, and they are in proportion. It is commonly applied in problems involving direct or inverse variation. For example, if a/b = c/d, you can find d by rearranging the equation to d = (b × c) / a.
| 5. How do you share a quantity in a given ratio? | |
Ans.To share a quantity in a given ratio, first, determine the total number of parts in the ratio. Then, divide the total quantity by the total parts to find the value of one part. Finally, multiply the value of one part by each part of the ratio to allocate the quantities accordingly. For example, for a ratio of 2:3 sharing a total of 50 units, each part is 10 units, resulting in 20 units for the first and 30 units for the second.
About this Document
4.68/5
Rating
Sep 11, 2025
Last updated
Related Exams
Document Description: Important Formula: Proportional Reasoning-1 for Class 8 2025 is part of Mathematics Class 8- New NCERT (Ganita Prakash) preparation.
The notes and questions for Important Formula: Proportional Reasoning-1 have been prepared according to the Class 8 exam syllabus. Information about Important Formula: Proportional Reasoning-1 covers topics
like Proportional Change, Ratios, Proportion, Rule of Three (Trairasika), Sharing in a Given Ratio, Unit Conversions and Important Formula: Proportional Reasoning-1 Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Formula: Proportional Reasoning-1.
Introduction of Important Formula: Proportional Reasoning-1 in English is available as part of our Mathematics Class 8- New NCERT (Ganita Prakash)
for Class 8 & Important Formula: Proportional Reasoning-1 in Hindi for Mathematics Class 8- New NCERT (Ganita Prakash) course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Important Formula: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash)
Description
Full syllabus notes, lecture & questions for Important Formula: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash) - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 8- New NCERT (Ganita Prakash) | Best notes, free PDF download
Information about Important Formula: Proportional Reasoning-1
In this doc you can find the meaning of Important Formula: Proportional Reasoning-1 defined & explained in the simplest way possible. Besides explaining types of
Important Formula: Proportional Reasoning-1 theory, EduRev gives you an ample number of questions to practice Important Formula: Proportional Reasoning-1 tests, examples and also practice Class 8
tests
Related Searches
Summary
,shortcuts and tricks
,Important questions
,Free
,Extra Questions
,Important Formula: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash)
,Objective type Questions
,Important Formula: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash)
,past year papers
,practice quizzes
,video lectures
,Previous Year Questions with Solutions
,mock tests for examination
,study material
,Sample Paper
,Exam
,Important Formula: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash)
,Semester Notes
,Viva Questions
,MCQs
,ppt
;
Additional Information about Important Formula: Proportional Reasoning-1 for Class 8 Preparation
Important Formula: Proportional Reasoning-1 Free PDF Download
The Important Formula: Proportional Reasoning-1 is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Important Formula: Proportional Reasoning-1 now and kickstart your journey towards success in the Class 8 exam.
Importance of Important Formula: Proportional Reasoning-1
The importance of Important Formula: Proportional Reasoning-1 cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Important Formula: Proportional Reasoning-1 Notes
Important Formula: Proportional Reasoning-1 Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Important Formula: Proportional Reasoning-1.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Important Formula: Proportional Reasoning-1 Notes on EduRev are your ultimate resource for success.
Important Formula: Proportional Reasoning-1 Class 8 Questions
The "Important Formula: Proportional Reasoning-1 Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Important Formula: Proportional Reasoning-1 on the App
Students of Class 8 can study Important Formula: Proportional Reasoning-1 alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Important Formula: Proportional Reasoning-1,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Important Formula: Proportional Reasoning-1 is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup