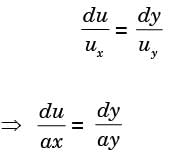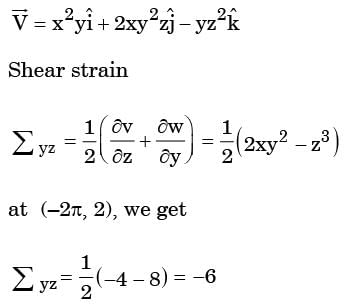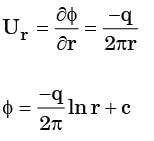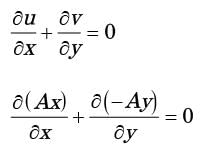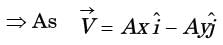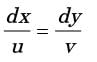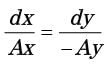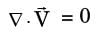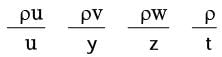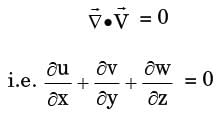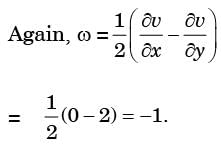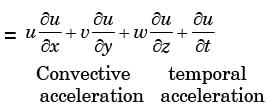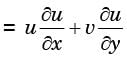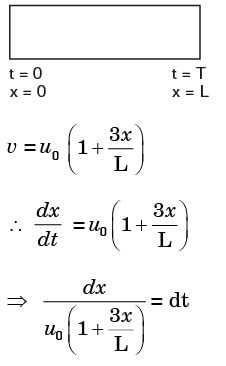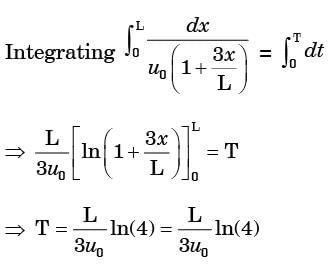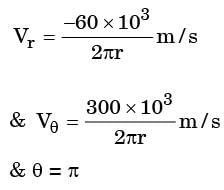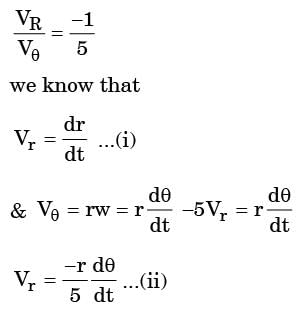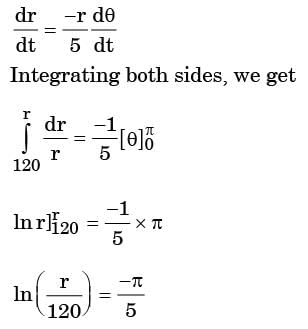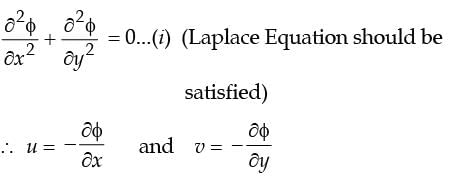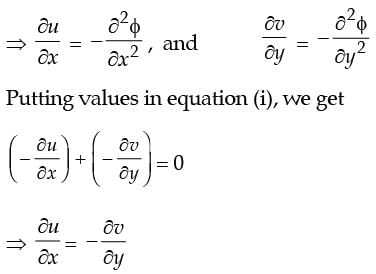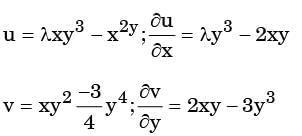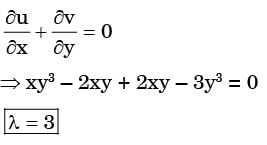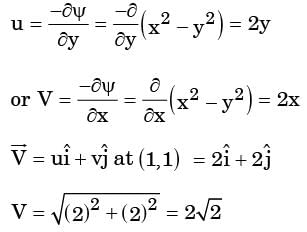GATE Past Year Questions: Fluid Kinematics | Fluid Mechanics for Mechanical Engineering PDF Download
Q1: The velocity field of a two-dimensional, incompressible flow is given by
 where
where  and
and 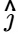 denote the unit vectors in x and y directions, respectively. If v (x, 0) = cos x, then v (0, -1) is [GATE ME 2024]
denote the unit vectors in x and y directions, respectively. If v (x, 0) = cos x, then v (0, -1) is [GATE ME 2024]
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c)
For an incompressible flow, ∇⋅ 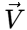 = 0
= 0
Given; the velocity field of a two-dimensional, incompressible flow,
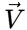 2 sinh
2 sinh 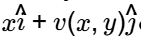 & v (x, 0) = cosh x
& v (x, 0) = cosh x
Now, ∇. 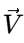 = 0 (for an incompressible flow)
= 0 (for an incompressible flow)
i. e. ∂v/∂x + ∂v/∂y = 0
2 cosh x + ∂v/∂y = 0
⇒ ∂v = -2 cos h . ∂y
Integrate both sides,
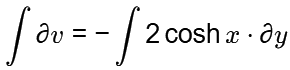
v = -2y cosh x + C.... (1)
Given; v (x, 0) = cosh x
⇒ C = cosh x
Now, from equation (1)
v (x, y)=−2y cosh x + cosh x
= (1−2y) cosh x
At (0,−1)
v (0,−1) = [1−2(−1)] cosh (0) = 3
Q1: Consider a unidirectional fluid flow with the velocity field given by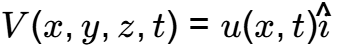
where u ( 0 , t ) = 1. If the spatially homogeneous density field varies with time t as
ρ (t)=1 + 0.2e −t the value of u (2 , 1) is _______. (Rounded off to two decimal places)
Assume all quantities to be dimensionless. [GATE ME 2023]
Ans: (1.1 to 1.2)
Continuity equation for unsteady flow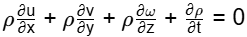 Here V (x, y, z, t)=u (x, t)
Here V (x, y, z, t)=u (x, t) 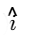
So v = 0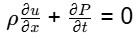
Given ρ(t)=1 + 0.2 e−t
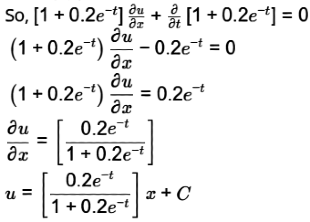
Since
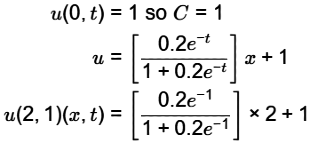
u (2, 1) = 1.137 m/s ≈ 1.14 m/sec
Q2: The velocity field of a certain two-dimensional flow is given by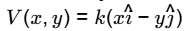
where k = 2s− 1 . The coordinates x and y are in meters. Assume gravitational effects to be negligible. If the density of the fluid is 1000 kg / m3 and the pressure at the origin is 100 kPa, the pressure at the location (2 m, 2 m) is _____________ kPa. (Answer in integer) [GATE ME 2023]
Ans: (83.999 to 84.001
To find the pressure at location (2m,2m) we apply Bernoulli's equation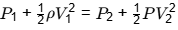
We will apply this equation between two points Origin(0, 0) and location (2 m, 2 m)
At Origin (0, 0)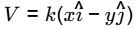
V1 =2 (0 − 0) = 0
P1 =100kPa
At Iocation (2, 2)
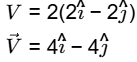
magnitude of velocity
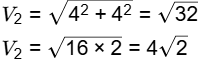
Applying Bernoulli's theorem
100,000 + 1/2 × 1000 × 0 = P2 + 1/2 × 1000 ×32
So P2 + 16,000 = 100,000
P2 = 100,000 −16,000
P2 = 84 , 000 Pa = 84 k Pa
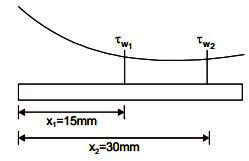
Q3: Air (density = 1.2kg/m3 , kinematic viscosity = 1. 5 × 1 0 − 5 m2/ s ) flows over a flat plate with a free-stream velocity of 2 m/s . The wall shear stress at a location 15mm from the leading edge is τ w . What is the wall shear stress at a location 30mm from the leading edge? [GATE ME 2023]
(a) Tw/2
(b) 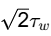
(c) 2/Tw
(d) 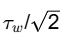
Ans: (d)
Step-1: First check type of flow by Reynold No
Re ∝ u ∞ L/v
Re = 2 x 0.03/1.5 x 10-5 = 4000
As Reynold no. is less than 5 × 1 05 , it is laminar flow
Step-2: Wall shear stress in laminar flow -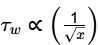
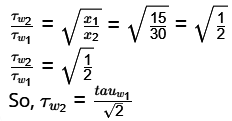
Q1: The steady velocity field in an inviscid fluid of density 1.5 is given to be 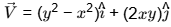 Neglecting body forces, the pressure gradient at (x = 1, y = 1) is [GATE ME 2022, SET-2]
Neglecting body forces, the pressure gradient at (x = 1, y = 1) is [GATE ME 2022, SET-2]
(a) 
(b) 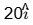
(c) 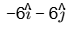
(d) 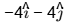
Ans: (c)
By Euler's equation of motion,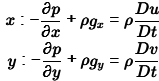
Neglecting body forces (i.e. g x = g y = 0 )
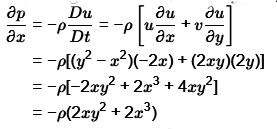
= - 1.5 x (2 x 1 x 12 + 2 x 13)
= - 6 pa/m
Similarly,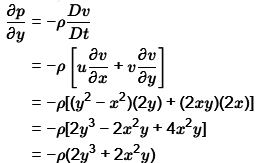
= - 1.5 x (2 x 1 x 12 + 2 x 13)
= - 6 pa/m
The pressure gradient vector is given by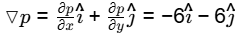
Q2:The velocity field in a fluid is given to be
Which of the following statement(s) is/are correct? [GATE ME 2022 SET-2]
(a) The velocity field is one-dimensional.
(b) The flow is incompressible
(c) The flow is irrotational
(d) The acceleration experienced by a fluid particle is zero at (x = 0, y = 0).
Ans: (b, c, d)
For given flow,
u = 4 xy, v = 2 (x2 − y2)
As velocity field is function of two space variables, flow is two dimensional.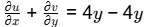
Therefore, flow is incompressible.
ω z = 1/2 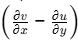 = 1/2 (4x - 4x) = 0
= 1/2 (4x - 4x) = 0
Therefore, flow is irrotational.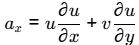
= 4 xy (4y) + 2 (x2 − y2) (4x)
= 16 xy2 + 8x 3 - 8xy2
= 16 x 0 x 02 + 8 x 03 - 8 x 0 x 02
= 0 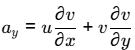
= 4 xy (4x) + 2 (x2 − y2) ( - 4y)
= 16 x2y - 8x 2 + 8xy3
= 16 x 0 x 02 x 8 x 02 x 0 + 8 x 03
= 0
 0
0
Q3: A steady two-dimensional flow field is specified by the stream function
ψ = kx3y
where x and y are in meter and the constant k = 1 m− 2 s− 1. The magnitude of acceleration at a point ( x , y ) = ( 1 m , 1 m ) is ________ m/s2 (round off to 2 decimal places). [GATE ME 2022, SET- 1]
Ans: (4.2 to 4.28)
Given,
Stream function,
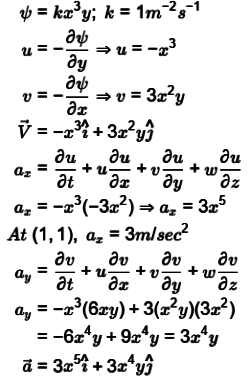
At (1, 1)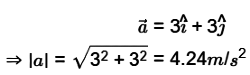
Q1: A two dimensional flow has velocities in x x and y y directions given by u = 2xyt and v = − y 2t , where t denotes time. The equation for streamline passing through x = 1 , y = 1 is [GATE ME 2021, SET-2]
(a) x2y = 1
(b) xy2 = 1
(c) x2y2 = 1
(d) x/y2 = 1
Ans: (b)
u = 2xyt
v = -y2t
dx/u = dy/v = dz/w
-ydx = 2xdy
In xy2= c
xy2 = 1
Q2: For a two-dimensional, incompressible flow having velocity components u and v in the x and y directions, respectively, the expression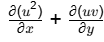
can be simplified to [GATE ME 2021, SET-2]
(a) u 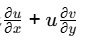
(b) 2u 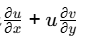
(c) 2u 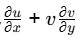
(d) u 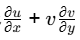
Ans: (d) 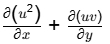
By differentiating: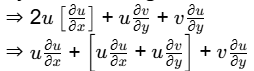
According to Continuity eq. : 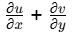 = 0
= 0
So, u 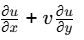
Q1: Consider a flow through a nozzle, as shown in the figure below: [GATE ME 2020, SET-2]
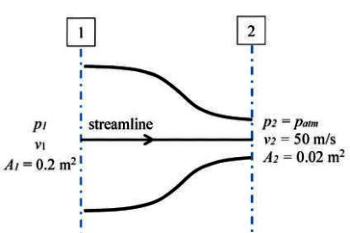 Ans: (1.5 to 1.55)
Ans: (1.5 to 1.55)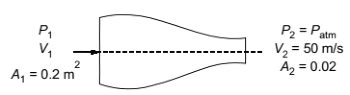
A1 V1 = A2 V2
0.2 x V1 = 0.02 x 50
V1 = 1/10 x 50 = 5m/s
Applying BE
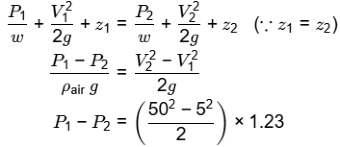
= 1522.125Pa = 1.52kPa
Q2: The velocity field of an incompressible flow in a Cartesian system is represented by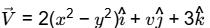
Which one of the following expressions for v is valid? [GATE ME 2020, SET-1]
(a) - 4 xz + 6xy
(b) - 4 xy + 6xz
(c) 4 xz + 6xy
(d) 4 xy + 6xz
Ans: (b) 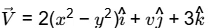
For Incompressible flow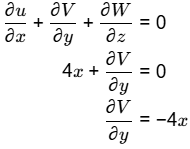
v = -4xy + f (x, z)
f (x, z) is an arbitary function of x and z
Hence the most suitable answer is option (B)
[2016, Set-3]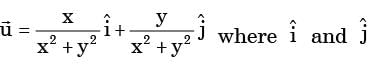 are the basis vectors in the x – y Cartesian coordinate system. Identify the CORRECT statements from below.
are the basis vectors in the x – y Cartesian coordinate system. Identify the CORRECT statements from below.
1. The flow is incompressible
2. The flow is unsteady
3. y-component of acceleration,
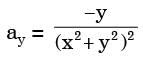
4. x-component of acceleration,
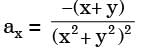
[2019, Set -2]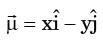 . If ρ is the density of the fluid, the expression for pressure gradient vector at any point in the flow field is given as
. If ρ is the density of the fluid, the expression for pressure gradient vector at any point in the flow field is given as
[2017 Set-1]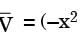
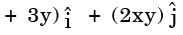 . The magnitude of the acceleration of a particle at (1, - 1) is
. The magnitude of the acceleration of a particle at (1, - 1) is
[2016,Set-3]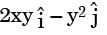 . The streamlines for this flow are given by the family of curves
. The streamlines for this flow are given by the family of curves
[2014 Set-4]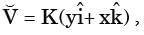 where K is a constant. The vorticity, Ω Z, is
where K is a constant. The vorticity, Ω Z, is
[2011]
[2006]
[2004]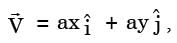 , where a is a constant. The equation of stream line passing through a point (1, 2) is
, where a is a constant. The equation of stream line passing through a point (1, 2) is
[1994]
[1988]

The rate shear deformation ∈yz at the point x = -2, y = -1 and z = 2 for the given flow is
[1987]
[1987]
[2018, Set-1]
[2018, Set-1]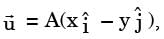 , where A > 0, which one of the following statements is FALSE?
, where A > 0, which one of the following statements is FALSE?
A. It satisfies continuity equation B. It is unidirectional when x → 0 and y → ∞.
C. Its streamlines are given by x = y.
D. It is irrotational
[2015: Set-1]

[2014, Set-2]
[2008]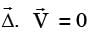 to be valid, where
to be valid, where 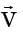 is the velocity vector,which one of the following is a necessary condition?
is the velocity vector,which one of the following is a necessary condition?
[2007]
P : Shear stress is zero at all points in the flow.
Q : Vorticity is zero at all points in the flow.
R : Velocity is directly proportional to the radius from the centre of the vortex.
S : Total mechanical energy per unit mass is constant in the entire flow field.
Select the correct answer using the codes given below:
[2001]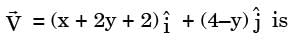
[1994]
[1994]
[1994]
Which one of the following conditions needs to be satisfied for the flow to be incompressible? [2017: Set-1]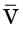 = (5 + a1x + +b1y)
= (5 + a1x + +b1y) 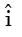 + (4 + a2x + b2y)
+ (4 + a2x + b2y) 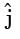 , where a1, b1, a2 and b2 are constants.
, where a1, b1, a2 and b2 are constants.
[2014 Set-4]
[2006]
[2007]
[2005]
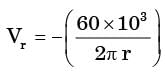 m/s and
m/s and 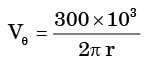 m/s, where r (in meters) is thedistance from the centre of the whirlpool. What will be the distance of the leaf from the centre when it has moved through half a revolution?
m/s, where r (in meters) is thedistance from the centre of the whirlpool. What will be the distance of the leaf from the centre when it has moved through half a revolution?
[2005]
[1995]
[1989]
|
56 videos|154 docs|75 tests
|
FAQs on GATE Past Year Questions: Fluid Kinematics - Fluid Mechanics for Mechanical Engineering
| 1. What are the key concepts in Fluid Kinematics relevant for GATE Civil Engineering? |  |
| 2. How is the continuity equation applied in Fluid Kinematics? |  |
| 3. What is the difference between laminar and turbulent flow? |  |
| 4. How can streamlines be used to analyze fluid flow? |  |
| 5. What role does velocity potential play in Fluid Kinematics? |  |

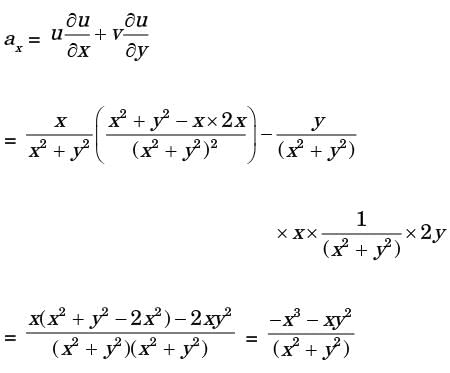
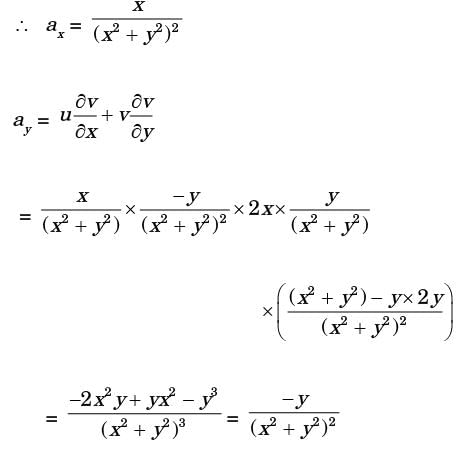
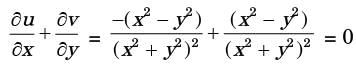
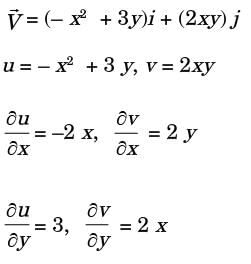


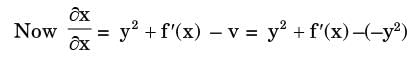 = y1 + f'(x)
= y1 + f'(x)
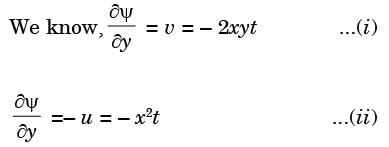 Integrating equation (i), we get
Integrating equation (i), we get