Discrete Fourier Transform (DFT) | Network Theory (Electric Circuits) - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Introduction to Discrete Fourier Transform (DFT) |

|
| Properties of DFT |

|
| Applications of DFT |

|
| Practical Considerations |

|
| Conclusion |

|
Introduction to Discrete Fourier Transform (DFT)
The Discrete Fourier Transform (DFT) is a powerful mathematical tool used to analyze the frequency content of a discrete signal. It is widely used in many fields like signal processing, image processing, and audio engineering. It transforms a sequence of complex numbers, which are sampled from a continuous-time signal, into another sequence that represents the same signal in the frequency domain.
Definition of DFT:
Given a sequence of complex numbers, the DFT of the sequence is defined as:
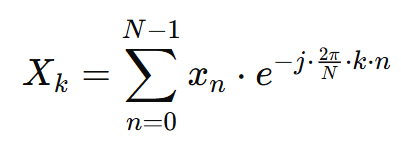
Where:
is the frequency-domain representation.
is the time-domain sequence.
is the number of samples in the sequence.
is the imaginary unit.
is the frequency index.
Inverse DFT (IDFT):
The Inverse DFT is used to convert a signal back from the frequency domain to the time domain. The IDFT is given by:
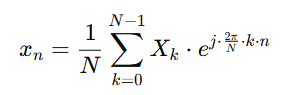
Properties of DFT
- Linearity: The DFT is a linear operation. That means, for two sequences x1[n]and x2[n], and constants a and b, the DFT of their linear combination is:
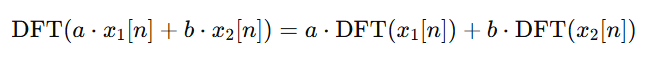
- Periodicity:
The DFT is periodic with a period . That is: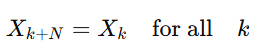
- Symmetry:
If is a real-valued sequence, the DFT of exhibits conjugate symmetry. This means: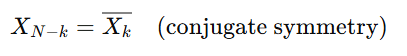
- Time and Frequency Shifting:
Time Shifting: If the sequence is shifted by units in time, the DFT of results in a phase shift in the frequency domain.
Frequency Shifting: A shift in the frequency domain corresponds to a time shift in the time domain.
Convolution Theorem:
The DFT of the convolution of two sequences is the pointwise product of their individual DFTs. Mathematically: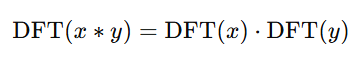
Applications of DFT
Signal Processing:
DFT is widely used in signal processing for analyzing the frequency components of signals. It is used in applications like filtering, modulation, and noise reduction.Image Processing:
In image processing, DFT is applied to analyze the frequency content of images, enabling operations like compression, noise removal, and edge detection.Audio Processing:
DFT is used in audio applications like MP3 compression, where it helps in transforming audio signals into a frequency domain to remove unnecessary components and reduce file sizes.Speech Recognition:
DFT is used to extract the spectral features of speech signals for automatic speech recognition systems.Data Compression:
DFT plays a key role in data compression techniques, such as JPEG for images and MP3 for audio, by removing the frequency components that are less perceptible to humans.
Fast Fourier Transform (FFT):
The FFT is an optimized algorithm used to compute the DFT with a reduced computational cost. While the DFT has a complexity of , the FFT reduces it to O(NlogN), making it more efficient for real-time applications.
Windowing in DFT:
In practical applications, signals are often finite and not periodic. To mitigate the issues arising from discontinuities at the boundaries (known as spectral leakage), windowing functions (like Hamming, Hanning, and Blackman-Harris) are applied to the signal before computing the DFT. These windows smooth the signal, reducing spectral leakage.
Frequency Resolution and Trade-offs:
The frequency resolution of the DFT depends on the length of the input sequence and the sampling rate. A longer sequence provides better resolution, but it comes with a trade-off in terms of increased computational cost and time. This trade-off is important in real-time signal processing.
Practical Considerations
Aliasing and Sampling Theorem:
The Nyquist-Shannon sampling theorem dictates that for an accurate DFT analysis, the sampling rate must be at least twice the highest frequency present in the signal. This is known as the Nyquist rate. If the signal is sampled below the Nyquist rate, aliasing occurs, leading to distortion in the frequency domain representation.Zero Padding:
Zero-padding is the process of adding zeros to the end of a signal to increase the length of the sequence before performing the DFT. This doesn’t increase the actual resolution but helps in making the result appear smoother, and can be useful in visualizing frequency components more clearly.
Conclusion
The Discrete Fourier Transform (DFT) is a fundamental tool in digital signal processing and various fields like communication, image processing, and audio analysis. It provides a way to analyze the frequency content of discrete-time signals and is essential for many real-time applications. The DFT, along with techniques like the Fast Fourier Transform (FFT), makes it possible to handle large-scale data efficiently.
Incorporating techniques such as windowing, zero-padding, and understanding the sampling theorem are crucial for obtaining accurate and practical results when working with DFT in real-world applications.
|
76 videos|152 docs|62 tests
|




















