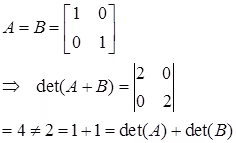Determinants | Engineering Mathematics - Engineering Mathematics PDF Download
| Table of contents |

|
| Determinant |

|
| Properties of Determinant |

|
| Efficient method to compute determinant |

|
| Inverse of Matrix |

|
Determinant
A square matrix is a matrix where the number of rows and columns are equal, that is a matrix of size n by n or n×n. The number associated with each square matrix is called the determinant of the matrix and tells us whether the matrix is invertible or not. Generally in this chapter, a matrix will mean a square matrix.
Determinant and Inverse of a 2 by 2 Matrix:
We first find the determinant of a 2 × 2 matrix and then expand to 3 × 3, .., n × n size matrices.
Example 1: Consider the general 2 × 2 matrix 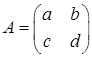 and the matrix
and the matrix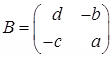 . Evaluate AB.
. Evaluate AB.
Solution: 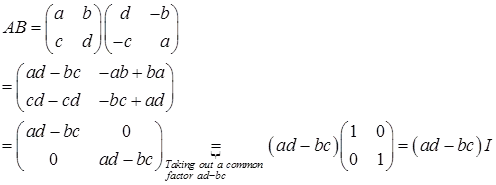
The matrix multiplication AB gives a multiple ad-bc of the identity matrix, I. This multiple (ad-bc) is called the determinant of matrix 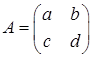 .
.
The determinant of a matrix A is normally denoted by det(A) or |A| and is a scalar not a matrix.
Hence the determinant of the general 2×2 matrix 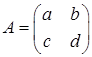 is defined as (2.1) det(A) = ad - bc
is defined as (2.1) det(A) = ad - bc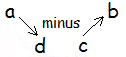
The determinant of a 2 × 2 matrix is the result of multiplying the entries of the leading diagonal and subtracting the product of the other diagonal. Remember the leading diagonal are the entries of the matrix which slope downwards to the right.
Example 2: Again consider the 2 × 2 matrices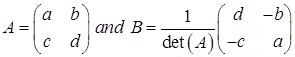
Evaluate the matrix multiplication AB provided det(A) ≠ 0.
Solution: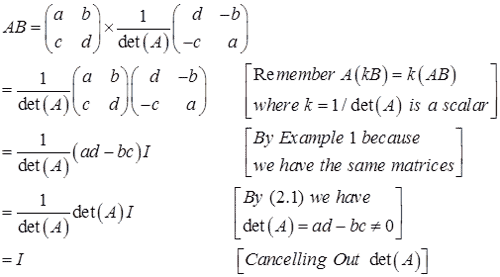
Note that the matrix multiplication AB gives the identity matrix 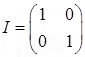 .
.
Since AB = I, what conclusions can we draw about the matrices A and B?
The given matrix 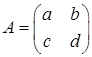 has an inverse matrix
has an inverse matrix  because
because
we have AB = I which means B is the inverse of matrix A, that is B = A-1.
Hence the inverse of the general 2 × 2 matrix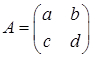 is given by
is given by
(2.2) 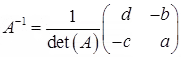 provided det(A) ≠ 0
provided det(A) ≠ 0
Q. What does this formula mean?
Ans: The inverse of a 2 × 2 matrix is determined by interchanging entries along the leading diagonal and placing a negative sign in the other and then multiplying this matrix by 1/det(A).
Q. What can we say if the determinant is zero, that is det(A) = 0?
Ans: If det(A) = 0 then the matrix A is non-invertible (singular), it has no inverse.
Example 3: Find the inverses of the following matrices:
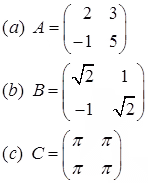
Solution:
(a) Before we can find the inverse we need to evaluate the determinant. Why?
Because if the determinant is 0 then the matrix does not have an inverse. Therefore by
(2.1) 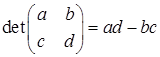

we have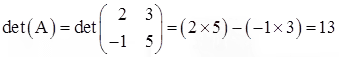
The inverse matrix A-1 is given by the above formula (2.2) with det(A) = 13: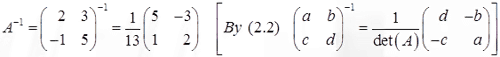
(b) We adopt the same procedure as part (a) to find B-1. By
(2.1) 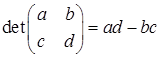
we have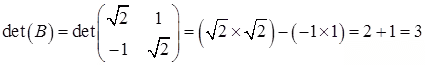
By substituting (B)=3 into the inverse formula (2.2) we have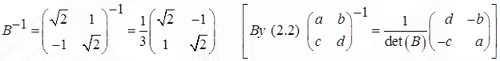
(c) Similarly applying (2.1) det(C) = ad-bc we have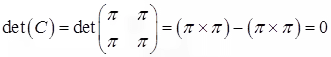
Q. What can we conclude about the matrix C?
Ans: Since det(C) = 0 therefore the matrix C is non-invertible (singular). This means it does not have an inverse.
Properties of Determinant
Let A be a n × n matrix.
- det(A) = det(AT)
- If two rows (or columns) of A are equal, then det(A) = 0.
- If a row (or column) of A consists entirely of 0, then det(A) = 0
Example:
Let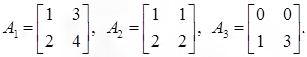 .
.
Then,
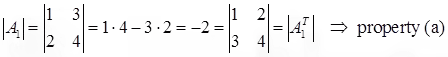
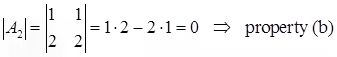
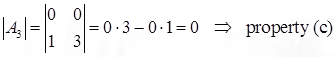
(d) If B result from the matrix A by interchanging two rows (or columns) of A, then det(B) = -det(A).
(e) If B results from A by multiplying a row (or column) of A by a real number c, rowi(B)-c *rowi(A) (or coli(B) = c *coli(A)), for some i, then det(B) = c *det(A).
(f) If B results from A by adding c*rows(A) (or c*cols(A)) to rowr(A) (or colr(A)), i.e., rowr(B) = rowr(A) + c*rows(A) (or colr(B) = colr(A) + c*cols(A)), then det(B) = det(A)
Example:
Let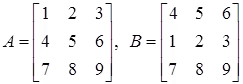
Since B results from A by interchanging the first two rows of A,
|A| = -|B| ⇒ property (d)
Example:
Let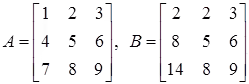
|B|= 2|A| ⇒ property (e),
Since col1(B) = 2 * col1(A)
Example:
Let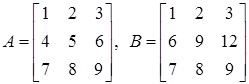
|A| = |B| ⇒ property (f),
Since row2(B) = row2(A) + 2 * row1(A)
(g) If a matrix 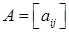 is upper triangular (or lower triangular), then
is upper triangular (or lower triangular), then
det(A) = a11a22… ann.
(h) det(AB) = det(A) det(B)
If A is nonsingular, then 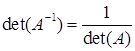
(i) det(cA) = cn det(A)
Example:
Let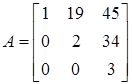
⇒ det(A) = 1∙2∙3 = 6 property(g)
Example:
Let
Then,
property (g)
Example:
Let
⇒ det(A) = 1∙4 - 3∙2 = -2, det(B) = 0
Thus,
det(AB) = det(A)det(B) = -2∙0 = 0 property(h)
and
Example:
Let
⇒ det(100A) = 1002 det(A) = 10000(-2) = -20000
property (i)
Example: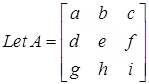
if det(A) = -7, then
Compute: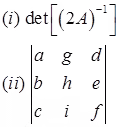
Solution: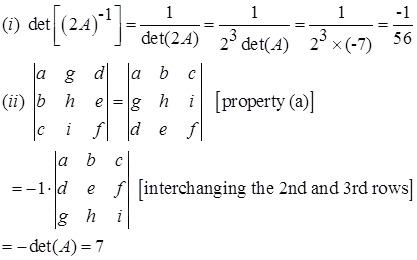
(j) For n × n square matrices P, Q, and X,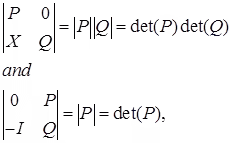
where I is an identity matrix.
Example:
Let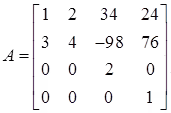
Then,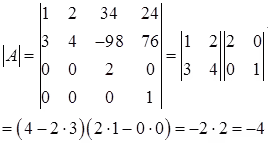
property (j)
Efficient method to compute determinant
To calculate the determinant of a complex matrix A, a more efficient method is to transform the matrix into a upper triangular matrix or a lower triangular matrix via elementary row operations. Then, the determinant of A is the product of the diagonal elements of the upper triangular matrix.
To calculate the determinant of a complex matrix A, a more efficient method is to transform the matrix into a upper triangular matrix or a lower triangular matrix via elementary row operations. Then, the determinant of A is the product of the diagonal elements of the upper triangular matrix.
Example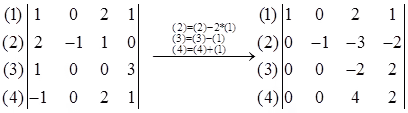
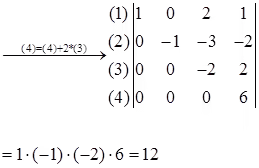
Note: det(A+B) is not necessarily equal to det(A) + det(B). For example,
Inverse of Matrix
The inverse (or reciprocal) of a square matrix is denoted by the A-1, and is defined by
A × A-1=I
For example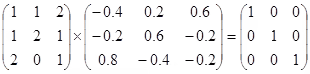
The 2 matrices as shown are inverses of each other, whose product is the identity matrix. Not all matrices have an inverse, and those which don’t are called singular matrices.
After the previous slightly complex definitions, the calculation of the inverse matrix is relatively simple.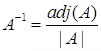
Clearly, if the determinant of A is zero, the inverse cannot be calculated and the matrix is said to be singular.
Inversion of 3 × 3 Matrix:
To find inverse of 3 × 3 matrix, First need to calculate determinant
Corresponding to each aij is a co-factor Cij.
9 elements in 3 × 3 ⇒ 9 co-factors.
Co-factor Cij = determinant of 2 x 2 matrix obtained by deleting row i and column j of A, prefixed by + or – according to following pattern.
Example:
C23 is co-factor associated with a23, in row 2 and column 3.
So delete row 2 and column 3 to give a 2 x 2 matrix
Co-factor C23 is – determinant of 2X2 matrix (negative sign in position a23)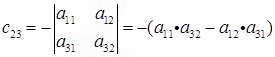
Example: Find all co-factors of matrix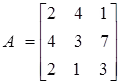
C11 = (delete row 1 column 1, compute determinant of remaining 2X2 matrix, position a11 associated with +)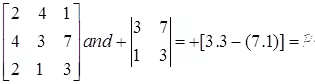
C12 = (delete row 1 column 2, compute determinant of remaining 2X2 matrix, position a21 associated with -)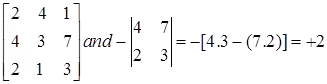
Other co-factors compute as follows: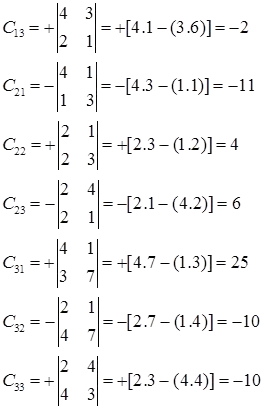
Co-factor Matrix 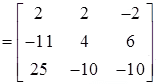
Now we can find the determinant,
Multiply elements in any one row or any one column by corresponding co-factors, and sum…..
Select row 1:
|A| = a11.C11 + a12.C12 + a13.C13
or equivalently select column 2
|A| = a12.C12 + a22.C22 + a32.C32
so the determinant of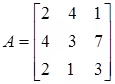
|A| = a21.C21 + a22.C22 + a23.C23
= (4.-11) + (3.4) + (7.6) = 10
Now we can find the Inverse……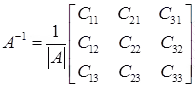
Step 1: write matrix of co-factors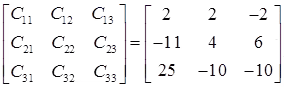
Step 2: transpose that matrix (replace rows by columns), so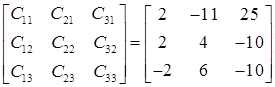
Step 3: multiply each element by 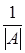
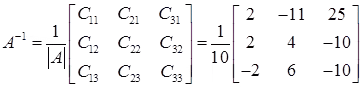
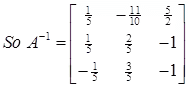
|
65 videos|133 docs|94 tests
|
FAQs on Determinants - Engineering Mathematics - Engineering Mathematics
| 1. What is the determinant of a matrix? |  |
| 2. What are some properties of determinants? |  |
| 3. What is an efficient method to compute the determinant of a matrix? |  |
| 4. How can determinants be used to find the inverse of a matrix? |  |
| 5. What are some common applications of determinants in mathematics? |  |