Cheatsheet: Linear Inequalities | Quantitative Aptitude for CA Foundation PDF Download
What is a Linear Inequality?
A linear inequality is similar to a linear equation, but instead of an equals sign (=), it uses inequality signs, such as <, >, <=, or >=. It represents a region of solutions rather than exact points.
Examples of Linear Inequalities
- One variable: x > 0, x ≤ 5
- Two variables: 3x + y ≤ 6, x - y ≥ -2
Graphing a Linear Inequality
- Replace the inequality with an equality and draw the line.
- Use a solid line for ≤ or ≥, and dashed line for < or >.
- Test a point (usually the origin) to determine which side to shade.
- The shaded area represents the solution space.
Convert to equality: y = 6 - 3x
Plot (0,6) and (2,0); then shade below the line since y < 6 - 3x
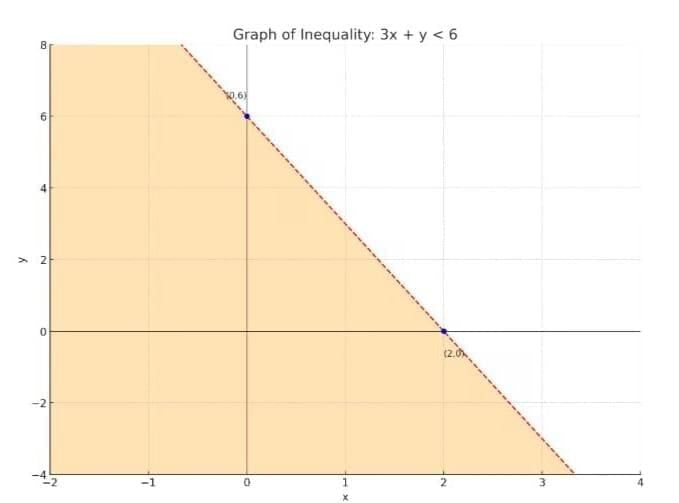
Step 1: Convert to equality → 3x + y = 6 → y = 6 - 3x
Step 2: Plot points (0,6) and (2,0) to draw the dashed boundary line
Step 3: Since it’s ‘<’, shade below the line (strict inequality)
Note: Dashed line indicates the boundary is not included
System of Inequalities
A system of inequalities includes two or more inequalities. The solution set is the region where all shaded areas overlap.
3x + y ≤ 6
x - y ≤ -2
x ≥ 0, y ≥ 0
Plot all four, and find the overlapping shaded region (feasible region).
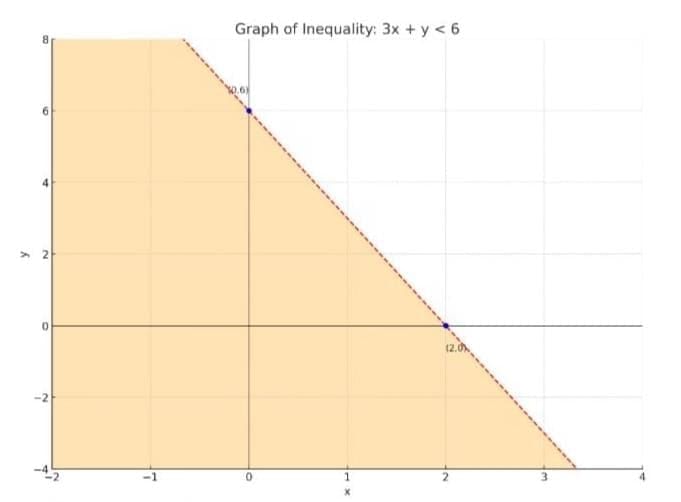
Step 1: Start with the inequality: 3x + y < 6
Step 2: Convert it to equality to find the boundary line:
3x + y = 6 → y = 6 - 3x
Step 3: Find two points on the line:
When x = 0, y = 6 → (0, 6)
When x = 2, y = 0 → (2, 0)
Step 4: Plot these points and draw a dashed line through them
(dashed because the inequality is ‘<’, not ‘≤’)
Step 5: Shade the region below the line since the inequality is y < 6 - 3x
Final: The shaded area represents all solutions to the inequality.
Feasible Region & Optimal Solution
- The region satisfying all constraints is the feasible region.
- It is bounded if enclosed, and unbounded if open-ended.
- Extreme points (corners) of this region help find max/min of an objective function.
- To maximise Z = ax + by, evaluate Z at all corner points.
Objective Function & Matrix Method
Let matrix E contain corner points, and C be the coefficient vector of the objective function.
Multiply: EC to get function values. The max/Min value of EC gives the optimal point.
C = [1, 2]
E = [[0,0], [6,0], [5,7], [0,7]]
Z-values = 0, 6, 19, 14 → Max = 19 at (5,7)
Solution:
Goal: Maximize Z = x + 2y
Coefficient Vector: C = [1, 2]
Corner Points Matrix E:
E = [[0, 0],
[6, 0],
[5, 7],
[0, 7]]
Step 1: Multiply E and C to get Z values:
Z = E × C = [0, 6, 19, 14]
Step 2: Identify the optimal value:
Maximum Z = 19 at point (5, 7)
Optimal Solution: Max Z = 19 at (5, 7)
Word Problems to Inequalities
- Translate constraints into inequalities.
- Identify objective (maximise profit, minimise cost).
- Examples: resource limits, time restrictions, production mix.
Maximise profit Z = 5x + 2y subject to:
2x + 6y ≤ 24
6x + 2y ≤ 24
x ≥ 0, y ≥ 0
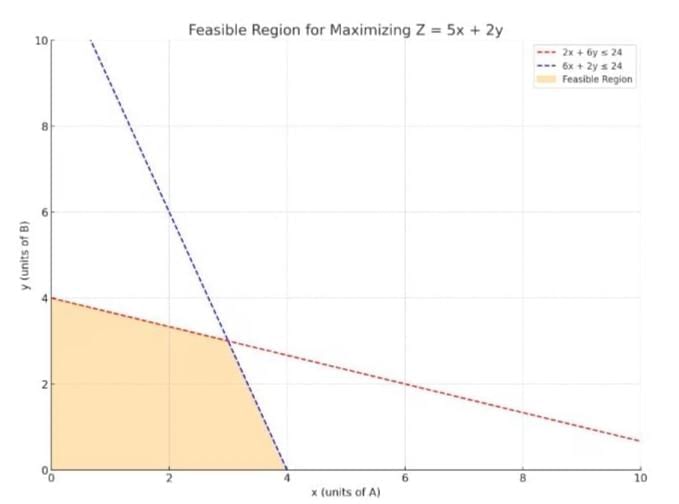
Step 1: Define variables:
Let x = units of A, y = units of B
Step 2: Write constraints from time usage:
Machine M1: 2x + 6y ≤ 24
Machine M2: 6x + 2y ≤ 24
Also: x ≥ 0, y ≥ 0 (non-negativity)
Step 3: Objective Function:
Maximize Z = 5x + 2y (profit)
Step 4: Graph the inequalities and identify feasible region
(Area that satisfies all constraints)
|
101 videos|267 docs|89 tests
|
FAQs on Cheatsheet: Linear Inequalities - Quantitative Aptitude for CA Foundation
| 1. What is a linear inequality? |  |
| 2. How do you graph a linear inequality? |  |
| 3. What is a system of inequalities? |  |
| 4. What is a feasible region in the context of linear inequalities? |  |
| 5. What is an objective function in linear programming? |  |
















