Class 8 Exam > Class 8 Notes > Mathematics Class 8 ICSE > Chapter notes: Rational Numbers
Chapter notes: Rational Numbers | Mathematics Class 8 ICSE PDF Download
Introduction
Rational numbers are important numbers used in real life. This chapter introduces rational numbers, their properties, and operations like addition, subtraction, multiplication, and division. It also covers how to represent rational numbers on a number line and find the rational numbers between two given numbers. These notes provide a clear, step-by-step explanation of each concept to help you thoroughly understand rational numbers.
What are Rational Numbers
- Natural numbers are counting numbers: 1, 2, 3, 4, 5, and so on.
- Whole numbers include zero along with natural numbers: 0, 1, 2, 3, 4, 5, etc.
- Integers consist of negative natural numbers, zero, and positive natural numbers: ..., -3, -2, -1, 0, 1, 2, 3, ... .
- This chapter explores rational numbers and their operations in detail.
Rational Number
- A rational number is expressed as p/q, where p and q are integers and q != 0.
- Examples:
- -3/7 is a rational number because -3 and 7 are integers, and 7 is not zero.
- 15/22 is a rational number because 15 and 22 are integers, and 22 is not zero.
- Zero (0) is a rational number because it can be written as 0/1, 0/2, 0/-10, etc., where the denominator is not zero.
- All natural numbers, whole numbers, integers, and fractions are rational numbers.
- In a rational number p/q, p is the numerator, and q is the denominator.
- Example: In -8/15, numerator = -8, denominator = 15.
- Example: If the numerator = 5 and the denominator = -2, the rational number is 5/-2.
- A rational number is positive if both the numerator and the denominator have the same sign (both positive or both negative).
- Examples: 5/8, -5/-8 are positive.
- A rational number is negative if the numerator and denominator have opposite signs.
- Examples: -5/8, 5/-8 are negative.
- If m is a non-zero integer and p/q is a rational number, then:
- p/q = p*m/q*m.
- p/q = p÷m/q÷m.
- Both p*m/q*m and p÷m/q÷m are rational numbers equivalent to p/q.
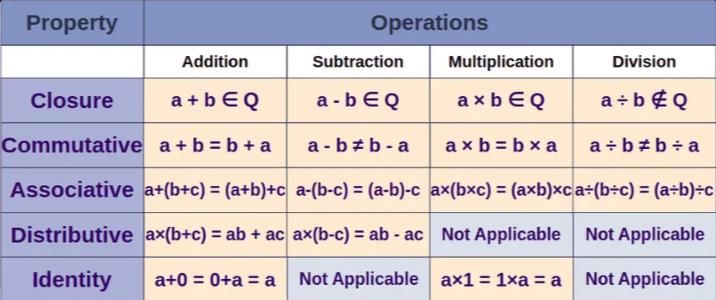
Properties of Addition of Rational Numbers
- Closure Property:
- Adding two rational numbers always results in a rational number.
- Example 1:3/4 + 5/6
- Find the LCM of denominators 4 and 6: LCM = 12.
- Rewrite: 3*3/4*3 + 5*2/6*2 = 9/12 + 10/12.
- Add: (9 + 10)/12 = 19/12, a rational number.
- Example 2:-3/8 + 5/12
- LCM of 8 and 12: LCM = 24.
- Rewrite: -3*3/8*3 + 5*2/12*2 = -9/24 + 10/24.
- Add: (-9 + 10)/24 = 1/24, a rational number.
- Commutative Property:
- Addition of rational numbers is commutative: a/b + c/d = c/d + a/b.
- Example:For -7/12 + 5/8:
- LCM of 12 and 8: LCM = 24.
- Left side: -7*2/12*2 + 5*3/8*3 = -14/24 + 15/24 = (-14 + 15)/24 = 1/24.
- Right side: 5*3/8*3 + -7*2/12*2 = 15/24 + -14/24 = (15 - 14)/24 = 1/24.
- Since 1/24 = 1/24, the property holds.
- Associative Property:
- Addition is associative: a/b + (c/d + e/f) = (a/b + c/d) + e/f.
- Example:For 2/3, -5/6, 7/12:
- Left side: 2/3 + (-5/6 + 7/12)
- Inside: LCM of 6 and 12 = 12.
- -5*2/6*2 + 7/12 = -10/12 + 7/12 = -3/12.
- Then: 2/3 + -3/12 = 8/12 + -3/12 = 5/12.
- Right side: (2/3 + -5/6) + 7/12
- Inside: LCM of 3 and 6 = 6.
- 2*2/3*2 + -5/6 = 4/6 + -5/6 = -1/6.
- Then: -1/6 + 7/12 = -2/12 + 7/12 = 5/12.
- Since 5/12 = 5/12, the property holds.
- Left side: 2/3 + (-5/6 + 7/12)
- Additive Identity:
- Zero (0) is the additive identity: a/b + 0 = 0 + a/b = a/b.
- Examples:
- 0 + -3/5 = -3/5 + 0 = -3/5.
- 0 + 7/8 = 7/8 + 0 = 7/8.
- Additive Inverse:
- The additive inverse of a/b is -a/b, and their sum is 0.
- Examples:
- Additive inverse of 3/5 is -3/5, and 3/5 + (-3/5) = 0.
- Additive inverse of -5/8 is 5/8, and -5/8 + 5/8 = 0.
Solved Examples
- (i) 7/15 + 3/5:
- LCM of 15 and 5 = 15.
- Rewrite: 7/15 + 3*3/5*3 = 7/15 + 9/15.
- Add: (7 + 9)/15 = 16/15, a rational number.
- (ii) 2/5 + 2:
- Write 2 as 2/1.
- LCM of 5 and 1 = 5.
- Rewrite: 2/5 + 2*5/1*5 = 2/5 + 10/5.
- Add: (2 + 10)/5 = 12/5, a rational number.
Subtraction of Rational Numbers
- Example 1: 5/6 - 3/4:
- LCM of 6 and 4 = 12.
- Rewrite: 5*2/6*2 - 3*3/4*3 = 10/12 - 9/12.
- Subtract: (10 - 9)/12 = 1/12.
- Example 2: -7/12 - (-5/8):
- Rewrite: -7/12 + 5/8.
- LCM of 12 and 8 = 24.
- Rewrite: -7*2/12*2 + 5*3/8*3 = -14/24 + 15/24.
- Add: (-14 + 15)/24 = 1/24.
Properties of Subtraction of Rational Numbers
- Closure Property:
- Subtracting two rational numbers results in a rational number.
- Example 1: 3/5 - 5/10 = 6/10 - 5/10 = 1/10, a rational number.
- Example 2: 7/12 - 5/18 = 21/36 - 10/36 = 11/36, a rational number.
- Commutative Property:
- Subtraction is not commutative: a/b - c/d != c/d - a/b.
- Example: -7/12 - 5/8 = -14/24 - 15/24 = -29/24.
- But 5/8 - -7/12 = 15/24 + 14/24 = 29/24.
- Since -29/24 != 29/24, subtraction is not commutative.
- Associative Property:
- Subtraction is not associative: a/b - (c/d - e/f) != (a/b - c/d) - e/f.
- Example:For 2/3, -5/6, 7/12:
- Left side: 2/3 - (-5/6 - 7/12) = 2/3 - (-10/12 - 7/12) = 2/3 + 17/12 = 25/12.
- Right side: (2/3 - -5/6) - 7/12 = (4/6 + 5/6) - 7/12 = 9/6 - 7/12 = 11/12.
- Since 25/12 != 11/12, subtraction is not associative.
- Identity:
- Only right identity exists: a/b - 0 = a/b, but 0 - a/b != a/b.
- Thus, subtraction has no identity.
- Inverse:
- Inverse for subtraction does not exist.
Multiplication of Rational Numbers
- Multiply numerators and denominators: a/b * c/d = a*c/b*d.
- Examples:
- 2/5 * 3/4 = 2*3/5*4 = 6/20 = 3/10.
- -3/5 * 4/7 = -3*4/5*7 = -12/35.
- -15/8 * -4/5 = (-15)*(-4)/8*5 = 60/40 = 3/2.
Properties of Multiplication of Rational Numbers
- Closure Property:
- Multiplying two rational numbers results in a rational number.
- Examples:
- 3/4 * 5/6 = 15/24 = 5/8, a rational number.
- -3/8 * 5/12 = -15/96 = -5/32, a rational number.
- Commutative Property:
- Multiplication is commutative: a/b * c/d = c/d * a/b.
- Example: -7/12 * 5/8 = -35/96, and 5/8 * -7/12 = -35/96.
- Associative Property:
- Multiplication is associative: a/b * (c/d * e/f) = (a/b * c/d) * e/f.
- Example:For 2/3, -5/6, 7/12:
- Left side: 2/3 * (-5/6 * 7/12) = 2/3 * -35/72 = -35/108.
- Right side: (2/3 * -5/6) * 7/12 = -5/9 * 7/12 = -35/108.
- Multiplicative Identity:
- One (1) is the multiplicative identity: a/b * 1 = 1 * a/b = a/b.
- Examples:
- 5/7 * 1 = 5/7.
- -20/47 * 1 = -20/47.
- Multiplicative Inverse:
- The multiplicative inverse of a/b is b/a, and their product is 1.
- Zero has no multiplicative inverse.
- Examples:
- Inverse of 3/5 is 5/3, and 3/5 * 5/3 = 1.
- Inverse of -5/8 is 8/-5, and -5/8 * 8/-5 = 1.
- 1 and -1 are their own multiplicative inverses.
- Distributive Property:
- Multiplication is distributive over addition: a/b * (c/d + e/f) = a/b * c/d + a/b * e/f.
- Example:3/4 * (-4/5 + 5/6):
- Left side: (-4*6 + 5*5)/30 = (-24 + 25)/30 = 1/30, so 3/4 * 1/30 = 1/40.
- Right side: 3/4 * -4/5 + 3/4 * 5/6 = -12/20 + 15/24 = -3/5 + 5/8 = 1/40.
Division of Rational Numbers
- Divide by multiplying by the reciprocal: a/b ÷ c/d = a/b * d/c, where c/d != 0.
- Division by zero is not defined.
- Examples:
- 3/4 ÷ 5/12 = 3/4 * 12/5 = 9/5.
- -6/7 ÷ 4/21 = -6/7 * 21/4 = -9/2.
- -16/27 ÷ -8/9 = -16/27 * 9/-8 = 2/3.
Properties of Division of Rational Numbers
- Closure Property:
- Dividing a rational number by a non-zero rational number results in a rational number.
- Examples:
- 3/4 ÷ 5/8 = 3/4 * 8/5 = 6/5, a rational number.
- 0 ÷ 5/2 = 0 * 2/5 = 0, a rational number.
- 4 ÷ 2/3 = 4 * 3/2 = 6, a rational number.
- Commutative Property:
- Division is not commutative: a/b ÷ c/d != c/d ÷ a/b.
- Associative Property:
- Division is not associative: a/b ÷ (c/d ÷ e/f) != (a/b ÷ c/d) ÷ e/f.
- Identity and Inverse:
- No identity or inverse exists for division.
Example: Product of Two Rational Numbers
- Product = 8/9, one number = -5/6, find the other.
- Other number = 8/9 ÷ -5/6 = 8/9 * -6/5 = -16/15.
Representation of Rational Numbers on the Number Line
- Draw a line and mark a point O for zero.
- Mark equal intervals on both sides of O.
- Right side points (A, B, C, ...) represent 1, 2, 3, ...
- Left side points (A', B', C', ...) represent -1, -2, -3, ...
- Example: Represent 1/2 and -3/2:
- Divide OA into 2 equal parts, mark P at 1/2.
- Move 3 halves left of O to mark Q at -3/2.
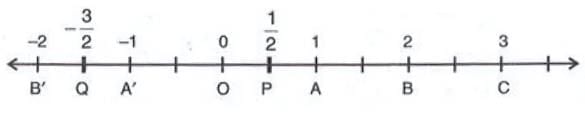
- Example: Represent -5/3 and 4/3:
- Divide OA and OA' into 3 equal parts.
- Move 5 parts left for -5/3, 4 parts right for 4/3.
Inserting Rational Numbers Between Two Given Rational Numbers
- First Method:
- Use the average: (a + b)/2, which lies between a and b.
- Example: One number between 2 and 3:
- (2 + 3)/2 = 5/2.
- Example: Two numbers between 7 and 8:
- First number: (7 + 8)/2 = 7.5.
- Second number: (7 + 7.5)/2 = 7.25 or (7.5 + 8)/2 = 7.75.
- Example: Three numbers between 3 and 4:
- First: (3 + 4)/2 = 3.5.
- Second: (3 + 3.5)/2 = 3.25.
- Third: (3.5 + 4)/2 = 3.75.
- Second Method:
- Use (a + c)/(b + d) for rational numbers a/b and c/d.
- Example: Three numbers between 3/5 and 4/7:
- First: (3 + 4)/(5 + 7) = 7/12.
- 3/5, 7/12, 4/7
- Again, using (a + c)/(b + d) for the second number between 3/5 and 7/12
- Second: (3 + 7)/(5 + 12) = 10/17.
- Third: (7 + 4)/(12 + 7) = 11/19.
- 3/5, 11/19, 10/17, 7/12, 4/7
The document Chapter notes: Rational Numbers | Mathematics Class 8 ICSE is a part of the Class 8 Course Mathematics Class 8 ICSE.
All you need of Class 8 at this link: Class 8
|
23 videos|123 docs|14 tests
|
FAQs on Chapter notes: Rational Numbers - Mathematics Class 8 ICSE
| 1. What are rational numbers and how are they defined? |  |
Ans. Rational numbers are numbers that can be expressed as the quotient or fraction of two integers, where the numerator is an integer and the denominator is a non-zero integer. In simpler terms, a rational number can be written in the form a/b, where 'a' and 'b' are integers and b ≠ 0.
| 2. What are the properties of addition of rational numbers? | |
Ans. The properties of addition of rational numbers include:
1. Commutative Property: a/b + c/d = c/d + a/b.
2. Associative Property: (a/b + c/d) + e/f = a/b + (c/d + e/f).
3. Identity Property: a/b + 0 = a/b.
4. Inverse Property: a/b + (-a/b) = 0.
| 3. How do you subtract rational numbers? | |
Ans. To subtract rational numbers, you need to find a common denominator if they have different denominators. Once you have the common denominator, you subtract the numerators while keeping the denominator the same. For example, to subtract 2/3 from 1/2, convert both fractions to have a common denominator (which is 6), giving you 1/2 = 3/6 and 2/3 = 4/6. Then, subtract: 3/6 - 4/6 = -1/6.
| 4. What are the properties of multiplication of rational numbers? | |
Ans. The properties of multiplication of rational numbers include:
1. Commutative Property: a/b × c/d = c/d × a/b.
2. Associative Property: (a/b × c/d) × e/f = a/b × (c/d × e/f).
3. Identity Property: a/b × 1 = a/b.
4. Zero Property: a/b × 0 = 0.
| 5. How is division of rational numbers performed? | |
Ans. To divide rational numbers, you multiply the first rational number by the reciprocal of the second rational number. For example, to divide 2/3 by 4/5, you would multiply 2/3 by the reciprocal of 4/5, which is 5/4. Thus, 2/3 ÷ 4/5 = 2/3 × 5/4 = 10/12, which simplifies to 5/6.
About this Document
4.64/5
Rating
Sep 11, 2025
Last updated
Related Exams
Document Description: Chapter notes: Rational Numbers for Class 8 2025 is part of Mathematics Class 8 ICSE preparation.
The notes and questions for Chapter notes: Rational Numbers have been prepared according to the Class 8 exam syllabus. Information about Chapter notes: Rational Numbers covers topics
like Introduction, What are Rational Numbers, Rational Number, Properties of Addition of Rational Numbers, Subtraction of Rational Numbers, Properties of Subtraction of Rational Numbers, Multiplication of Rational Numbers, Properties of Multiplication of Rational Numbers, Division of Rational Numbers, Properties of Division of Rational Numbers, Representation of Rational Numbers on the Number Line, Inserting Rational Numbers Between Two Given Rational Numbers and Chapter notes: Rational Numbers Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter notes: Rational Numbers.
Introduction of Chapter notes: Rational Numbers in English is available as part of our Mathematics Class 8 ICSE
for Class 8 & Chapter notes: Rational Numbers in Hindi for Mathematics Class 8 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Chapter notes: Rational Numbers | Mathematics Class 8 ICSE
Description
Full syllabus notes, lecture & questions for Chapter notes: Rational Numbers | Mathematics Class 8 ICSE - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 8 ICSE | Best notes, free PDF download
Information about Chapter notes: Rational Numbers
In this doc you can find the meaning of Chapter notes: Rational Numbers defined & explained in the simplest way possible. Besides explaining types of
Chapter notes: Rational Numbers theory, EduRev gives you an ample number of questions to practice Chapter notes: Rational Numbers tests, examples and also practice Class 8
tests
Related Searches
study material
,Free
,mock tests for examination
,practice quizzes
,Viva Questions
,Exam
,Sample Paper
,Important questions
,Summary
,Chapter notes: Rational Numbers | Mathematics Class 8 ICSE
,ppt
,Objective type Questions
,Extra Questions
,Semester Notes
,shortcuts and tricks
,past year papers
,Previous Year Questions with Solutions
,Chapter notes: Rational Numbers | Mathematics Class 8 ICSE
,MCQs
,video lectures
,Chapter notes: Rational Numbers | Mathematics Class 8 ICSE
;
Additional Information about Chapter notes: Rational Numbers for Class 8 Preparation
Chapter notes: Rational Numbers Free PDF Download
The Chapter notes: Rational Numbers is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter notes: Rational Numbers now and kickstart your journey towards success in the Class 8 exam.
Importance of Chapter notes: Rational Numbers
The importance of Chapter notes: Rational Numbers cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter notes: Rational Numbers
Chapter notes: Rational Numbers Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter notes: Rational Numbers.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter notes: Rational Numbers Notes on EduRev are your ultimate resource for success.
Chapter notes: Rational Numbers Class 8 Questions
The "Chapter notes: Rational Numbers Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter notes: Rational Numbers on the App
Students of Class 8 can study Chapter notes: Rational Numbers alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter notes: Rational Numbers,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter notes: Rational Numbers is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily