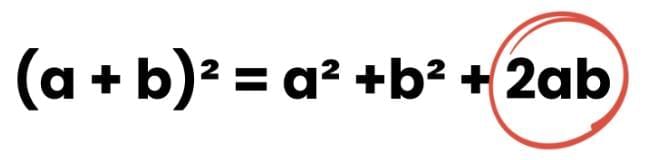We Distribute, Yet Things Multiply Chapter Notes | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Introduction
Algebra uses letter symbols to express patterns and relationships in a simple and compact way. It not only helps in writing general statements but also in proving properties and solving different kinds of problems.
One important property that connects multiplication and addition is distributivity. In this chapter, we will explore various multiplication patterns and learn how they can be expressed clearly in the language of algebra using the distributive property.
Some Properties of Multiplication
Increments in Products
When we multiply two numbers and change one or both of them, the product also changes. We can study how much the product increases when:
One number is increased by 1
Both numbers are increased by 1
To understand this, we make use of the distributive property of multiplication over addition.
Using Distributivity
Distributive Property of Multiplication over Addition
The distributive property states:
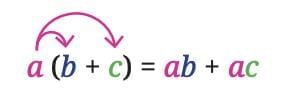
This means that when a number is multiplied by a sum, we can multiply it with each term and then add the results.
This property can be visualised nicely using a diagram: 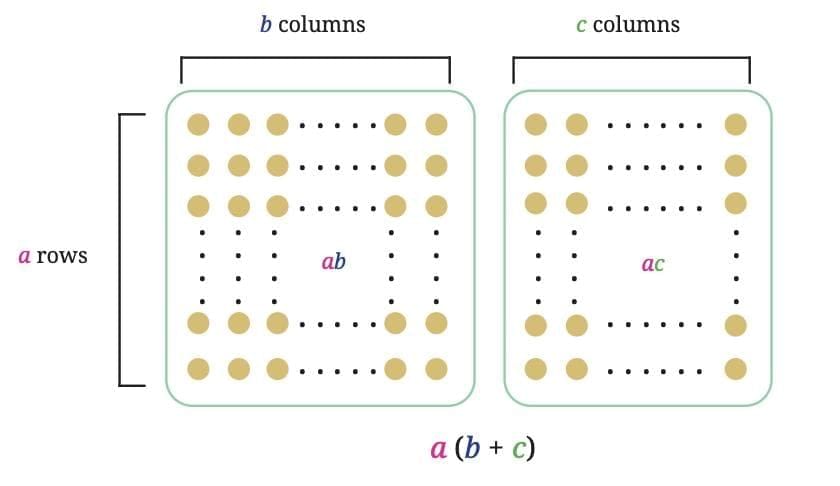
For example, let a = 23, b = 27, c = 1:
23 (27 + 1) = 23 × 27 + 23 × 1
= (original product) + 23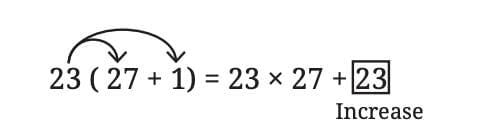
This shows that if one number (27) is increased by 1, the product increases by the other number (23).
Note: Distributivity in Action: Expanding (a + b)c
We can also expand an expression like (a + b)c using distributivity and commutativity:
(a + b) c = c (a + b) (commutativity of multiplication)
= ca + cb (distributivity)
= ac + bc (commutativity again)
This shows that multiplication can be broken down and rearranged easily.
General Cases of increase
If one number is increased by 1
a(b + 1) = ab + a
→ The product increases by a.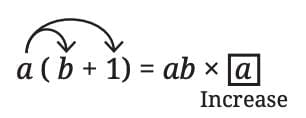
If both numbers are increased by 1
(a + 1)(b + 1) = ab + a + b + 1
→ The product increases by a + b + 1.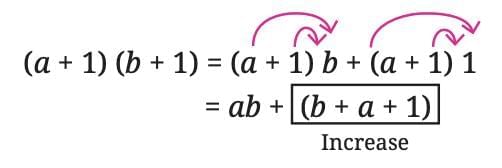 For example: If a = 23, and, b = 27, we get
For example: If a = 23, and, b = 27, we get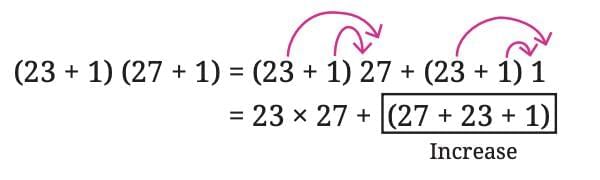
If one number increases by 1 and the other decreases by 1
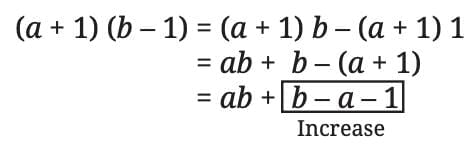 → Here, the product may increase or decrease, depending on the values of a and b.
→ Here, the product may increase or decrease, depending on the values of a and b.
For example: If a = 23, and, b = 27, we get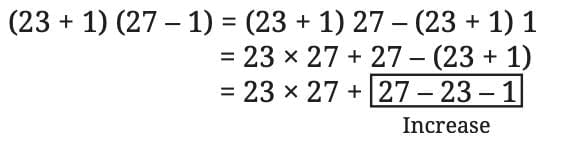
Lets Explore:
The distributive property holds true for all integers (positive, negative, or zero).
This means even if a and b are negative numbers, the same rules apply.
For example: If a = –5, b = 8 and c = 1, check if it holds true for a(b + c) = ab + ac.
–5 (8 + 1) = (-5 × 8) + (-5 × 1) = (-40) + (-5) = (-45)
we still get the same results using a(b + c) = ab + ac.So, the increase in products rule works for negative integers as well.
Algebraic Identities
When two algebraic expressions are equal for all values of their letters, they are called identities.
Examples:
a(b + 8) = ab + 8a
(a + 1)(b – 1) = ab + b – a – 1
These are true no matter what values a and b take.
General Case: Increase by m and n
If the first number increases by m and the second by n, then it becomes (a + m)(b + n)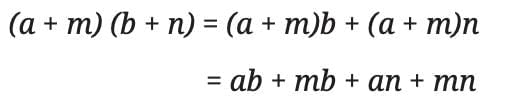
So, the increase in the product is:
an + bm + mn
The product is simply the sum of the products of each term in (a + m) multiplied by each term in (b + n).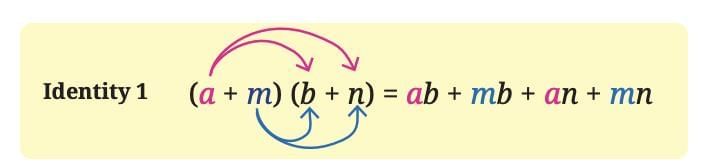 This shows that the distributive property allows us to break down and calculate changes in products systematically. This identity can be visualised as follows–
This shows that the distributive property allows us to break down and calculate changes in products systematically. This identity can be visualised as follows–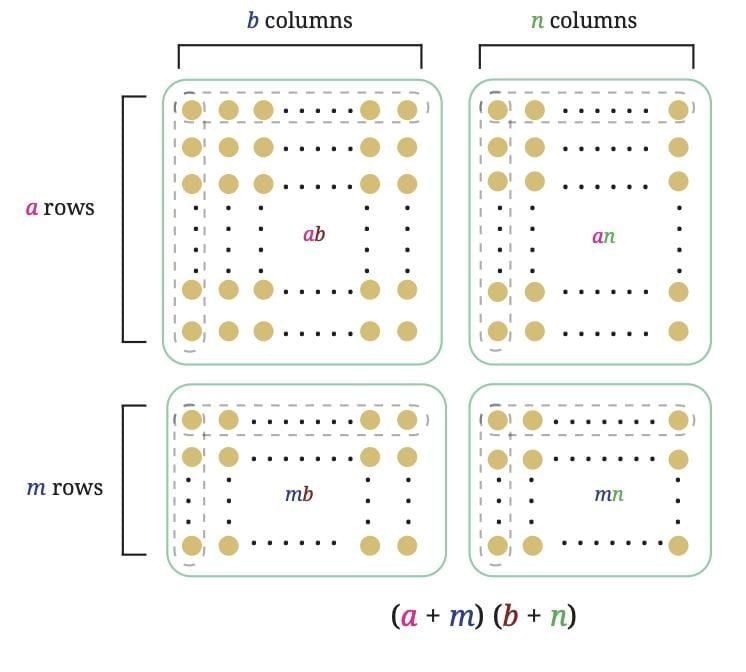
Lets Explore: One Number Increases by 1, the Other Decreases by 1
We can still use the same identity. A decrease means we take m or n as negative.
Write the product as:
(a + 1)(b – 1)
Here, m = 1 and n = –1.
Using the identity:= ab + (1)b + a(–1) + (1)(–1)
= ab + b – a – 1This matches the earlier result.
General Formula for Increase and Decrease
We can derive a general formula using algebra for cases where one number increases by u and the other decreases by v:
(a + u) (b – v)
Expanding using distributivity:
= (a + u)b – (a + u)v
= ab + ub – av – uv
So,
(a + u)(b – v) = ab + ub – av – uv
Key Observations
Taking m = u and n = –v in Identity 1 gives the same result.
Just like before, we multiply each term of (a + u) with each term of (b – v).
The signs of terms depend on integer multiplication rules (positive × negative = negative, etc.).

A Pinch of History
The distributive property (multiplying each term inside brackets and then adding the results) is not a modern discovery.
Long ago, mathematicians in Egypt, Mesopotamia, Greece, China, and India were already using it, even if they didn’t write it the way we do today.
Examples from History
Euclid (Greece): Used it in geometry by breaking shapes into smaller parts.
Āryabhaṭa (India): Used it in algebra for his scientific work.
First Clear Statement
Brahmagupta (7th century India):
First person to write the distributive property clearly in his book Brahmasphuṭasiddhānta.
He called it khaṇḍa-guṇanam, meaning multiplication by parts.
His method:
Break the multiplier into parts → multiply each part → then add the results.
In today’s algebra, this is the same as:
(a + b)c = ac + bc
In the very next verse, he also explained how this rule can be used for faster multiplication.
Fast Multiplications Using the Distributive Property
The distributive property can make multiplication with certain numbers (like 11, 101, 1001, etc.) much faster.
Example: Let’s take 3874 × 11.
We can write it as:
3874 × 11 = 3874 × (10 + 1)
= 3874 × 10 + 3874 × 1
= 38740 + 3874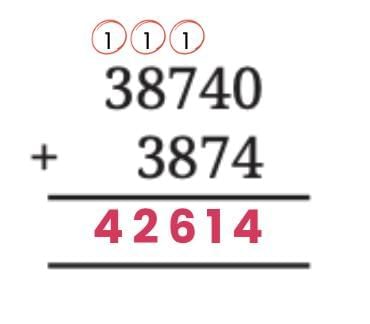
This is just splitting 11 into 10 + 1, multiplying separately, and then adding.
Notice how digits are adding up when we multiply by 11.
For a 4-digit number dcba (where d = thousands, c = hundreds, b = tens, a = ones):
dcba × 11 = dcba × (10 + 1)
= (dcba × 10) + (dcba)
When you write this out and add, the middle digits are the sum of the adjacent digits of the original number.
This becomes:
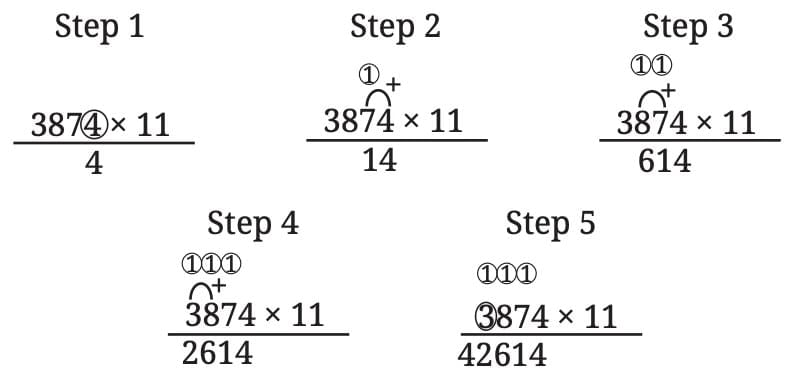
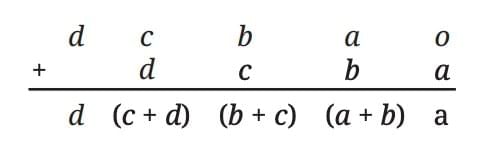 Continuing with our example, the above can be used to obtain the product in one line.
Continuing with our example, the above can be used to obtain the product in one line.
Special Cases of the Distributive Property
Square of the Sum/Difference of Two Numbers
This can be understood with the help of an example:
Area Representation of 65²
A square of side 65 can be understood by splitting the side into 60 + 5. This divides the big square into four regions: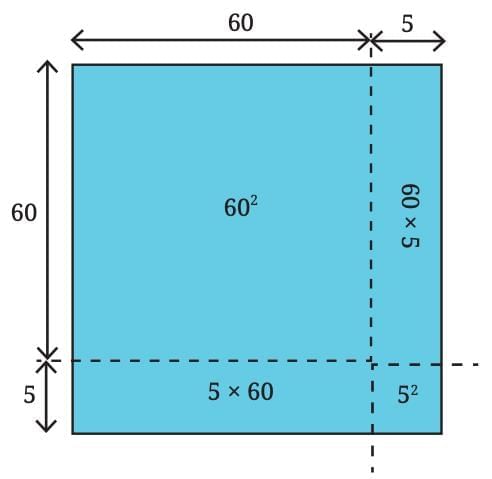
A square of side 60 → area = 60² = 3600
A square of side 5 → area = 5² = 25
Two rectangles, each 60 × 5 → total area = 2 × (60 × 5) = 600
Adding all the parts gives the total area:
65² = 60² + 5² + 2 × (60 × 5)
= 3600 + 25 + 600
= 4225
We can also use Distributive Expansion
Using distributivity:
(60 + 5)(60 + 5)
= (60 × 60) + (5 × 60) + (60 × 5) + (5 × 5)
= 60² + 2 × (60 × 5) + 5²This matches the area representation. The cross-terms (5 × 60 and 60 × 5) combine to give 2 × (60 × 5).
Let us device the general expression for the square of sum of two numbers, (a + b)2
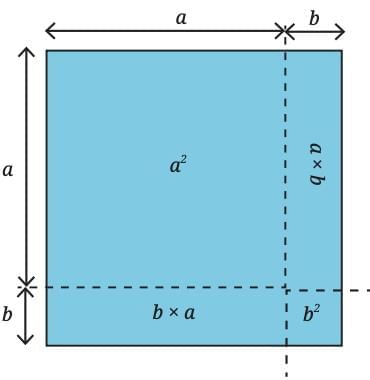
Using the distributive property, (a+b)2 can be expanded as
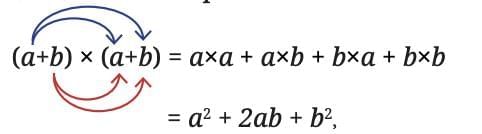
This creates the general algebraic identity: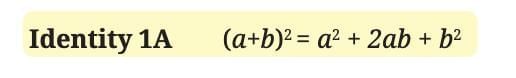
Lets Explore:
Comparing (a + b)² and a² + b²
From the identity:
(a + b)² = a² + 2ab + b²
The extra term compared to a² + b² is 2ab
Example: Expand (6x + 5)2

Square of a Difference
This can be understood with the help of an example:
To understand the expansion of (a – b)², we can take the example of finding (60 – 5)², which is the same as 55².
Instead of calculating directly, we use geometry to visualize and simplify the expression.
Draw a big square of side 60.
Inside it, draw a smaller square of side 55.
The difference in side lengths is 5.
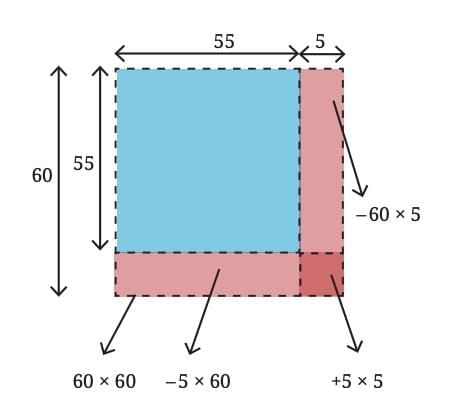
The area of the large square is 60². If we remove two rectangles each of size 60 × 5, we cut away more than required because the small corner square of side 5 has been subtracted twice. To correct this, we add back the area of the 5 × 5 square once.
Thus,
(60 – 5)² = 60² – (60 × 5) – (5 × 60) + 5²
Simplifying,
= 3600 – 300 – 300 + 25
= 3025
So, the area of the square with side 55 is 3025 square units.
This reasoning works in general. For any two numbers a and b:
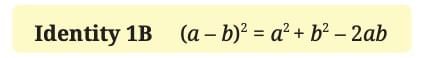
This identity shows that the square of a difference is obtained by squaring the first term, subtracting twice the product of the two terms, and adding the square of the second term.
Investigating Patterns
Pattern 1
Let’s look at these examples: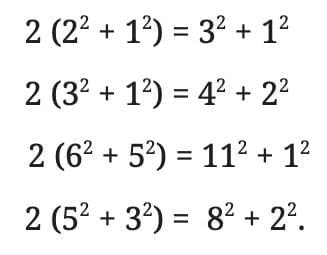
We are given a set of equations, where each is of the form a pattern.
Now, we test whether this pattern can be explained using algebraic identities.
We look at the following identity:
(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²
If we add these two identities together, we get:
(a + b)² + (a – b)²
= (a² + 2ab + b²) + (a² – 2ab + b²)
= 2a² + 2b²
This simplifies to:
2(a² + b²)
Thus, this proves the pattern, as it shows that:
2 × (a² + b²) = (a + b)² + (a – b)²
Example: 2 × (2² + 1²) = 3² + 1²
Left side: 2 × (4 + 1) = 2 × 5 = 10
Right side: 9 + 1 = 10
Identity check: Let a = 2, b = 1.
(2 + 1)² + (2 - 1)² = 3² + 1² = 9 + 1 = 10
2 × (2² + 1²) = 2 × (4 + 1) = 10
The identity holds, and the pattern matches.
Pattern 2
Let’s look at these examples:
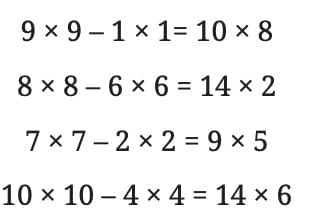
The observed pattern here is:
a² – b² = (a + b) × (a – b)
We need to check if this pattern always holds true using algebraic identities.
Verifying the Pattern Using Algebra
Let’s break down the identity using the distributive property:
(a + b) × (a – b) = a² – ab + ba – b²
Since ab + (–ab) = 0, we are left with:
a² – b²
This confirms that the identity is true, as we get the same result on both sides of the equation.
The Identity:
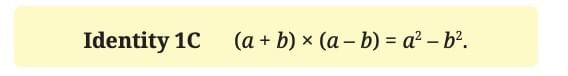
For example,
We can write 31² in the form of the identity above:
Let a = 31, b = 1
(31 + 1)(31 – 1) + 1²
= 32 × 30 + 1
= 960 + 1
= 961
Your Turn!
Question: Use this identity to quickly calculate the product.
1. 98 × 102 = ?
Hint: Write them as (100 – 2)(100 + 2)
Now apply the identity a² – b² = (a + b)(a – b).
 View Answer
View Answer 
Solution: Notice–
98 = 100 – 2
102 = 100 + 2
So, this is of the form: (a – b)(a + b) = a² – b²
Here, a = 100 and b = 2
Now apply the identity:
= 100² – 2²
= 10,000 – 4
= 9,996
2. 45 × 55 = ?
 View Answer
View Answer 
Solution: Here:
45 = 50 – 5
55 = 50 + 5
This is again of the form: (a – b)(a + b)
a = 50, b = 5
(50-5)(50+5)
Apply the identity:
= 50² – 5²
= 2,500 – 25
= 2,475
Geometric Interpretation
We can also geometrically show that: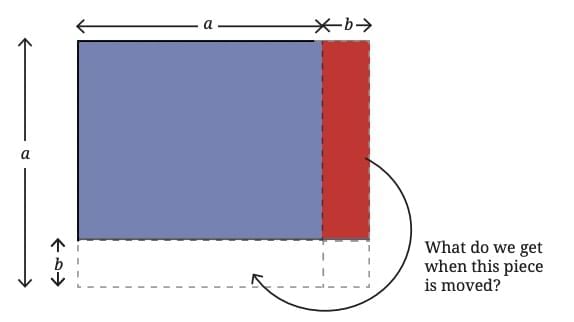
(a + b) × (a – b) = a² – b²
By using a geometric approach, such as representing the expressions as areas of squares or rectangles, we can visualize the subtraction of areas, leading to the same result.
Mind the Mistake, Mend the Mistake
We have expanded and simplified a few algebraic expressions to their simplest form.
Review each simplification carefully to check for any errors.
If you spot a mistake, try to understand and explain what went wrong.
After that, rewrite the expression correctly.

Think It Through – Then Check Your Answer
 View Answer
View Answer 
Algebraic Expression Corrections
1. Correct
Given: –3p(–5p + 2q)
= –3p × –5p + –3p × 2q
= 15p² – 6pq
Correct Answer: 15p² – 6pq
Mistake: Final simplification was written as p – 2q (wrong).
2. Incorrect
Given: 2(x – 1) + 3(x + 4)
= 2x – 2 + 3x + 12 = 5x + 10
Correct Answer: 5x + 10
Mistake: They wrote 5x + 3 (wrong).
3. Incorrect
Given: y + 2(y + 2)
= y + 2y + 4 = 3y + 4
Correct Answer: 3y + 4
Mistake: They expanded it like a square: (y + 2)² = y² + 4y + 4 (misinterpretation).
4. Incorrect
Given: (5m + 6n)²
Using identity: (a + b)² = a² + 2ab + b²
= 25m² + 60mn + 36n²
Correct Answer: 25m² + 60mn + 36n²
Mistake: Likely used a wrong expansion.
5. Incorrect
Given: (–q + 2)² = (2 – q)²
= 4 – 4q + q² = q² – 4q + 4
Correct Answer: q² – 4q + 4
Mistake: Steps or signs in simplification were incorrect.
6. Incorrect
Given: 3a(2b × 3c)
= 3a × 6bc = 18abc
Correct Answer: 18abc
Mistake: They wrote 54a²bc (wrong multiplication).
7. Incorrect (partially)
Given: ½(10s – 6) + 3
= 5s – 3 + 3 = 5s
Correct Answer: 5s
Mistake: Skipped proper simplification steps (even though final answer is correct).
8. Incorrect
Given: 5w² + 6w
Correct Answer: 5w² + 6w (cannot combine terms)
Mistake: They wrote 11w² (incorrectly added unlike terms).
9. Incorrect
Given: 2a³ + 3a³ + 6a²b + 6ab²
= 5a³ + 6a²b + 6ab²
Correct Answer: 5a³ + 6a²b + 6ab²
Mistake: They wrote 5a³ + 12a²b² (wrong combination).
10. Correct
Given: (x + 2)(x + 5)
= x² + 7x + 10
Correct Answer: x² + 7x + 10
11. Incorrect
Given: (a + 2)(b + 4)
= ab + 4a + 2b + 8
Correct Answer: ab + 4a + 2b + 8
Mistake: They wrote only ab + 8 (missed middle terms).
12. Incorrect
Given: ab + a²b + a²b²
= ab(1 + a + ab)
Correct Answer: ab(1 + a + ab)
Mistake: They factored as ab(a + b + ab) – which is incorrect.
This Way or That Way, All Ways Lead to the Bay
Look at the pattern shown in the figure.
We are looking at a sequence of figures that follow a specific pattern. Each figure in the sequence predictably adds more circles. There are multiple ways to approach this pattern: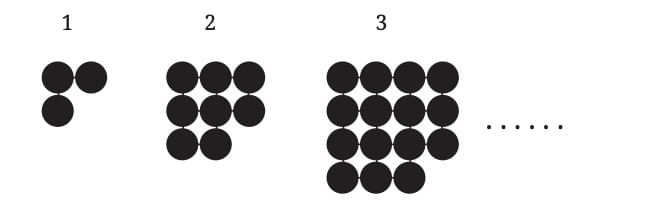
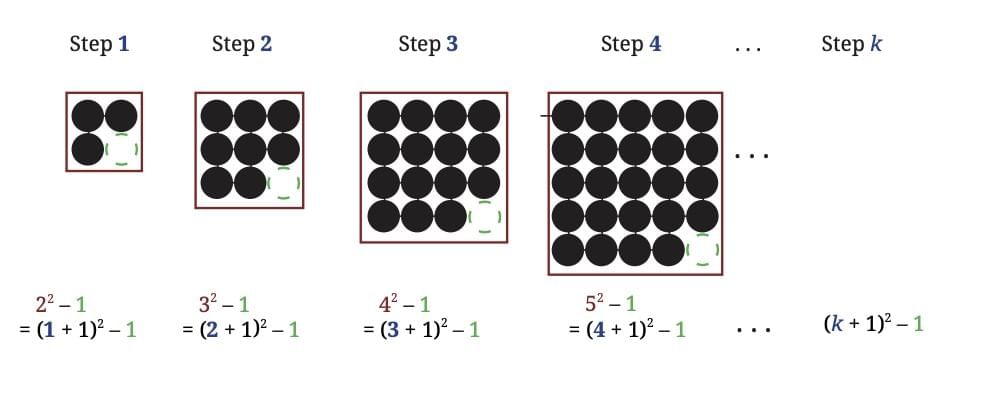
Method 1
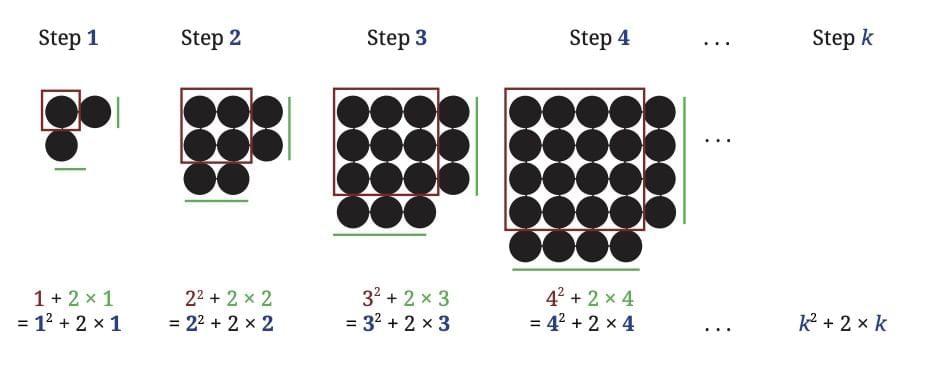
Method 2
Method 3
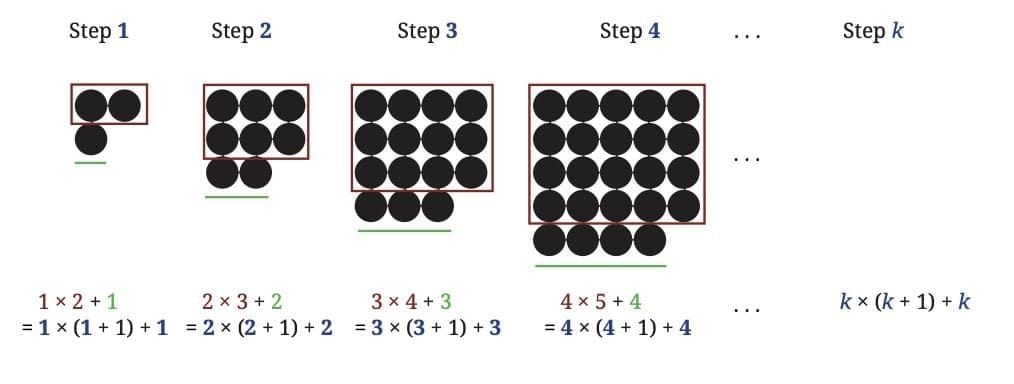 Method 4
Method 4
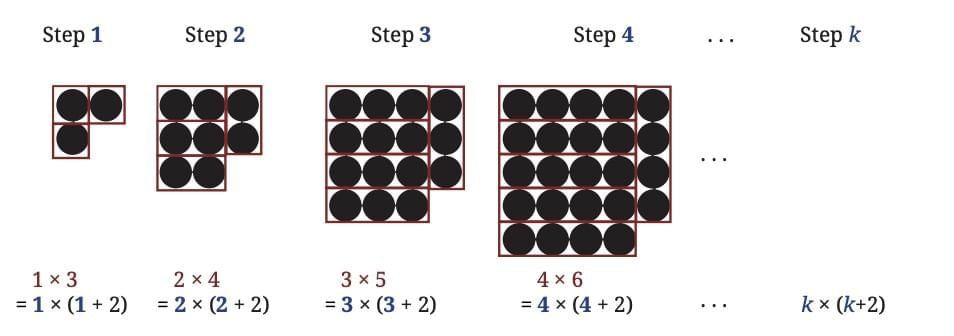
You may have used a method that matches one of the expressions shown, or perhaps a different approach altogether. While these expressions may appear different at first, they all describe the same pattern.
That means they should be mathematically equivalent. Let's simplify each expression to verify if they are indeed the same.

When carried out correctly, all methods lead to the same answer; k2 + 2k. The expression k2 + 2k gives the number of circles at Step k of this pattern

Note: Mathematics allows for multiple perspectives
- There isn't always just one right way to recognize or solve a problem.
- Different approaches can lead to the same result, and discovering them often involves thinking creatively and exploring new ideas.
- Some methods might feel more natural or easier than others, but trying out various strategies can help us see patterns more clearly and make learning more interesting.
|
13 videos|105 docs
|
FAQs on We Distribute, Yet Things Multiply Chapter Notes - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are the basic properties of multiplication that students should understand? |  |
| 2. How does the distributive property help in simplifying mathematical expressions? |  |
| 3. Can you provide an example of how to apply the commutative property of multiplication in a real-world scenario? |  |
| 4. Why is it important for students to learn the properties of multiplication? |  |
| 5. How can the associative property of multiplication be demonstrated using numbers? |  |