Transformations (Term 4) Chapter Notes | Mathematics for Grade 6 PDF Download
| Table of contents |

|
| Making Larger Copies of Figures |

|
| Enlargements and Reductions |

|
| Increasing the Lengths of Two Sides Only |

|
| Points to Remember |

|
| Difficult Words |

|
| Summary |

|
Making Larger Copies of Figures
This section teaches students how to enlarge shapes using scale factors while preserving their shape.
Understanding Enlargements
Enlargement: Creating a larger copy of a shape where all side lengths are multiplied by a scale factor, keeping the shape identical.
Example: Figures A, B, and C (each a combination of two quadrilaterals):
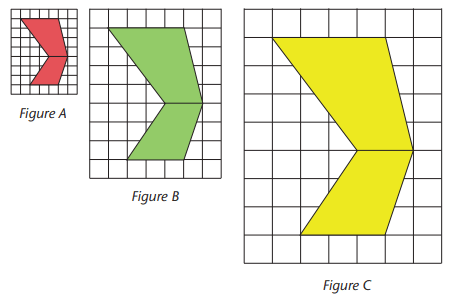
- Figure B is 2 times as large as Figure A (scale factor = 2).
- Figure C is 3 times as large as Figure A (scale factor = 3).
- Figure C is 1.5 times as large as Figure B (scale factor = 1.5, since 3 ÷ 2 = 1.5).
Key similarity: All figures have the same shape (proportions), but differ in size.
Key difference: Side lengths increase with the scale factor.
Enlarging on Grids
Use grid paper to enlarge shapes accurately:
Example: A kite on a 0.5 cm grid:
- Enlarge by scale factor 3: Draw on a 1.5 cm grid (0.5 × 3 = 1.5 cm).
- Enlarge by scale factor 2: Draw on a 1 cm grid (0.5 × 2 = 1 cm).
Method: Multiply each side length by the scale factor and draw on the appropriately scaled grid.
Scale Factor Application
To enlarge a shape:
- Scale factor 2: Double all side lengths (e.g., 1 cm becomes 2 cm).
- Scale factor 4: Quadruple all side lengths (e.g., 1 cm becomes 4 cm).
Shapes not proportionally scaled (e.g., different shapes) are not enlargements.
Enlargements and Reductions
This section expands on enlargements and introduces reductions, emphasizing proportional scaling.Enlargements vs. Non-Enlargements
Enlargement: All side lengths multiplied by the same scale factor, preserving shape.
Example: Rectangle C (12 cm × 9 cm) is an enlargement of Rectangle A (8 cm × 6 cm) by scale factor 1.5 (12 ÷ 8 = 9 ÷ 6 = 1.5).
Non-enlargement: Adding a fixed length to sides changes the shape.
- Example: Adding 16 units to all sides alters proportions, not an enlargement.
- Rebecca’s view: Correct—multiply side lengths by a scale factor (e.g., 3) to keep shape.
- Nkhangweleni’s view: Incorrect—adding fixed lengths changes shape.
Reduction: A smaller copy of a shape (scale factor < 1).
Example: Figure A is a reduction of Figure C by factor 1/3 (since C is 3 times A).
Reductions on Grids
Example: Yellow rhombus on a 1.5 cm grid:
- Reduction to 1.25 cm grid (scale factor = 1.25 ÷ 1.5 = 5/6).
- Reduction to 0.5 cm grid (scale factor = 0.5 ÷ 1.5 = 1/3).
Grid comparisons for quadrilaterals:
- Reduction by factor 5 from 1.25 cm grid: 1.25 ÷ 5 = 0.25 cm grid.
- 3/4 size of 1 cm grid: 1 × 3/4 = 0.75 cm grid.
- 3/5 size of 1.25 cm grid: 1.25 × 3/5 = 0.75 cm grid.
- 5/4 size of 1 cm grid: 1 × 5/4 = 1.25 cm grid.
- 4/3 size of 0.75 cm grid: 0.75 × 4/3 = 1 cm grid.
Scale Factor Relationships
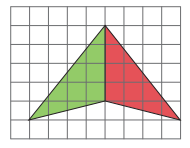
Example: Figures A, B, C (page 350):
- B is 2 times A (scale factor 2).
- B is not 3 times A or 2/3 of C (check proportions).
Enlargements/reductions of a quadrilateral:
- Scale factor 1.5: All sides × 1.5.
- Scale factor 2/3: All sides × 2/3.
- Scale factor 1 2/3: All sides × 5/3.
Side lengths and diagonals scale by the same factor as the figure.
Rectangles and Diagonals
Rectangle A: 8 cm × 6 cm.
Enlargements:
- B: 12 cm × 9 cm (scale factor 1.5).
- C: 16 cm × 12 cm (scale factor 2).
- D: 20 cm × 15 cm (scale factor 2.5).
- E: 24 cm × 18 cm (scale factor 3).
Diagonal: Line from a vertex to the opposite vertex, dividing a rectangle into two triangles.
Diagonals scale with the same factor (e.g., diagonal of B is 1.5 times A’s diagonal).
Check enlargements:
- 9 cm × 12 cm: Scale factor 1.5 (12 ÷ 8 = 1.5, 9 ÷ 6 = 1.5) → Enlargement.
- 12 cm × 16 cm: Scale factor 2 (16 ÷ 8 = 2, 12 ÷ 6 = 2) → Enlargement.
- 9 cm × 11 cm, 14 cm × 16 cm: Not enlargements (inconsistent scale factors).
Relationships:
- D is 2.5 times A.
- B is 1/3 of E (9 ÷ 18 = 12 ÷ 24 = 1/3).
- C is 0.5 times E (12 ÷ 24 = 16 ÷ 24 = 0.5).
Increasing the Lengths of Two Sides Only
This section explores scaling only two opposite sides of a rectangle, altering its shape.
Partial Scaling
Standard enlargement/reduction: Multiply all four sides by the same scale factor to preserve shape.
Partial scaling: Multiply only two opposite sides by a scale factor, changing the shape.
Example: Rectangle with sides 8 cm × 6 cm:
- Scale only lengths (8 cm) by 2: New rectangle 16 cm × 6 cm.
- Scale only widths (6 cm) by 2: New rectangle 8 cm × 12 cm.
Result: The shape is no longer proportional to the original (not an enlargement).
Effect on Shape
- Scaling two sides creates a new rectangle with different proportions.
- Example: Original 8 cm × 6 cm (ratio 4:3), scaling length to 16 cm gives 16 cm × 6 cm (ratio 8:3).
- This transformation is distinct from true enlargements/reductions.
Points to Remember
- Enlargement: Larger copy of a shape with all sides multiplied by a scale factor (e.g., 2, 3).
- Reduction: Smaller copy of a shape (scale factor < 1, e.g., 1/3).
- Scale factor: Number by which side lengths are multiplied (e.g., 1.5 for 12 cm ÷ 8 cm).
- Grid scaling: Use grids to enlarge/reduce (e.g., 0.5 cm to 1.5 cm for scale factor 3).
- Diagonal: Line dividing a rectangle into two triangles, scales with the same factor.
- Proportional scaling: Multiply all sides to keep shape (not adding fixed lengths).
- Partial scaling: Scaling only two sides changes the shape.
Difficult Words
- Transformation: Changing a shape’s size or position (e.g., enlargement).
- Enlargement: Making a shape larger by a scale factor.
- Reduction: Making a shape smaller by a scale factor.
- Scale factor: Number used to multiply side lengths (e.g., 2, 1/3).
- Quadrilateral: 2-D shape with four sides (e.g., rectangle, rhombus).
- Rhombus: Quadrilateral with all sides equal.
- Diagonal: Line from a vertex to the opposite vertex in a polygon.
Summary
This chapter equips Grade 6 students with skills to perform transformations by creating enlargements (e.g., scale factor 2 for 8 cm × 6 cm to 16 cm × 12 cm) and reductions (e.g., scale factor 1/3) of shapes like rectangles and rhombuses, using grids (e.g., 0.5 cm to 1.5 cm). Students learn that proportional scaling preserves shape, while scaling only two sides alters it, fostering an understanding of geometric similarity and measurement.FAQs on Transformations (Term 4) Chapter Notes - Mathematics for Grade 6
| 1. What are transformations in mathematics? |  |
| 2. How do you perform a translation on a graph? |  |
| 3. What is the difference between rotation and reflection? |  |
| 4. Can you give an example of a dilation? |  |
| 5. Why are transformations important in geometry? |  |



















