Three Dimensional Shapes Chapter Notes | Mathematics Class 6 (Maharashtra Board) PDF Download
| Table of contents |

|
| Introduction |

|
| Reflection and Symmetry |

|
| Section |

|
| Planes of Symmetry |

|
| Rotational Symmetry |

|
| No Rotational Symmetry |

|
| Nets |

|
Introduction
- Have you ever folded a paper heart perfectly in half and noticed both sides looked the same?
- Or spun a wheel and saw how it looks the same at different points as it turns?
- That’s the magic of symmetry!
- Symmetry is when an object or shape looks the same even after you flip, turn, or divide it in special ways.
Reflection and Symmetry
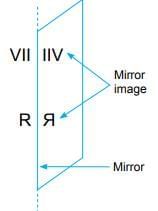
- Look at the mirror kept vertically.
- The figure in front of the mirror has a reflection image in the mirror.
- See the images of VII and R.
- The mirror image and the given original object are exactly symmetrical, the mirror line is the line of symmetry.
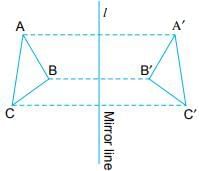
- No difference in length or breadth between the object and its image in the mirror.
- In the figure, ΔA'B'C' is the mirror image of ΔABC.
- The distances of A', B', C' from the mirror are the same as the distances of A, B, and C from the mirror.
- The farther the point from the mirror line, the farther will be its mirror image.
(ii) Also the length of 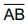 = length of
= length of 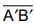 Also length of
Also length of 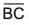 = length of
= length of 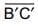 Also length of
Also length of 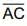 = length of
= length of 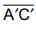 and ∠BAC = ∠B'A'C', ∠ABC = ∠A'B'C', ∠BCA = ∠B'C′A'.
and ∠BAC = ∠B'A'C', ∠ABC = ∠A'B'C', ∠BCA = ∠B'C′A'.
(iii) AA', BB' and CC' are perpendicular to the mirror line and are bisected by the mirror line.
- Mirrors are used in kaleidoscopes to produce images of the small pieces of bangles kept inside.
- A number of images are produced due to the number of mirrors used.
- This gives rise to different symmetrical designs in the kaleidoscope.
To Draw A Mirro Image of a Given Figure
Let ABCDE be a figure given to us whose mirror image is to be drawn.
We draw perpendiculars from the vertices of the given figure to the mirror line. AP, E4, DR, CS and BT are drawn perpendicular to the mirror line.
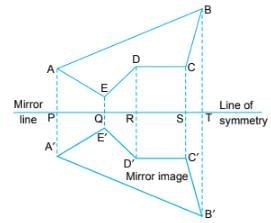
- Produce AP to A', E4 to E', DR to D', CS to C', BT to B' such that PA' = PA, QE' = QE, RD' = RD, SC' = SC and TB' = TB. Join A' – B' – C' – D' – E' in sequence to get the mirror image A'B'C'D'E' of the given figure ABCDE.
- The mirror line is the line of symmetry between these two figures.
To Complete a Figure With Two Lines of Symmetry
Let ABCDE be the given part of the figure and p, and q be the two lines of symmetry.
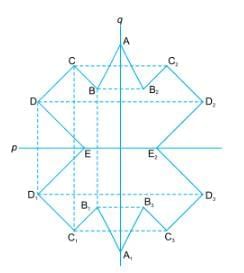
- By drawing perpendiculars from the corner points to lines p and q, we get the image points of the corner points of the given part of the figure.
- Joining them in sequence, we complete the figure which will have p and q as two lines of symmetry.
Section
- Imagine slicing directly through the centre of a cube, as illustrated in the image.
- The surface created by this cut, which is shaded in the image, is known as a section of the cube.
- In this example, the section forms a square.
.
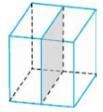
When we make a straight cut through a solid, we say that the solid is cut by a plane, i.e., the section is flat.
Planes of Symmetry
- A plane of symmetry divides a 3D shape into two congruent shapes.
- One shape must be a mirror image of the other shape.
- A shaded plane is a plane of symmetry of the cube.
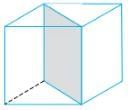
Imagine that a cuboid is cut into two pieces by a plane as shown below.
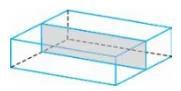
Now take one of the pieces and put the cut face against a mirror.
- Does the piece, together with its reflection, look like a complete solid?
- If it does, as happens in this case, then the cut has been made in a plane of symmetry.
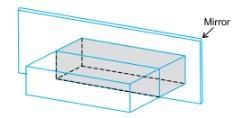
- Not all planes which cut a solid in half are planes of symmetry.
- The solid below has not been cut in a plane of symmetry.
- If one half is placed against a mirror, we do not see the complete solid.

Rotational Symmetry
- Observe the familiar figures of a line segment, equilateral triangle, square, etc.
- These figures have linear symmetry.
- They also possess another type of symmetry called rotational symmetry.
Example 1: Draw a line segment AB having a fixed length. Mark its mid-point O. Fix a pin through O. Now, keeping the middle point fixed, rotate the line segment AB about O. After a rotation of 180, you will find that the line segment takes position B1A1. Thus, the new position B1A1 fits into the original line segment AB.
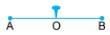
Another rotation of 180 about the central point O gives A1B1, a new position A2B2, once again fitting into the original line segment AB, A2 falling on A and B2 falling on B.
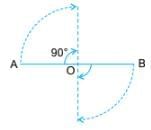
- During one rotation of 360 degrees about the midpoint O, the line segment fits into itself twice.
- This indicates that the line segment has rotational symmetry of order 2.
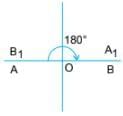
The midpoint of the line segment is the centre of rotation.
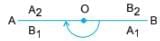
The point around which the figure is rotated is called the centre of rotation.
Thus, A figure has rotational symmetry, if there is a central point around which the figure is rotated through a certain number of degrees (less than 180) and the figure still looks the same. The central point is called the centre of rotation. The smallest angle we need to turn the figure to get a similar figure again is called the angle of rotation.
The number of times a shape will fit onto itself in one complete rotation is called the order of the rotational symmetry.
Edurev Tips: A full rotation does not mean that a figure has rotational symmetry because every shape could fit exactly into itself after a full (360º) rotation.
Example 2: Rotate an equilateral triangle about its centroid (the point where the medians meet) through an angle of 120º. After a rotation of 120º, 240º, 360º, the triangle gets three new positions of A1B1C1, A2B2C2 and A3B3C3 falling on BCA, CAB and ABC respectively.
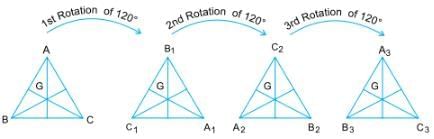
Thus, the triangle matches itself three times during a rotation of 360º. Therefore, it has rotational symmetry of order 3.
Here, the order of rotational symmetry = 360º/120º = 3
Example 3: Rotate a square about its centre (the point where its diagonals meet), through an angle of 90. After each rotation of 90, the new square fits into the original square, i.e., the square matches itself after a rotation of 90, 180, 270 and 360, i.e., 4 times during one complete rotation of 360.
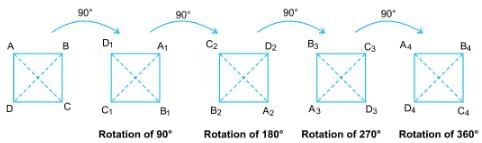
∴ Angle of rotation = 90º
Here, the order of rotation = 360º/90º = 4
In general, we have
Order of rotational symmetry = 360º/the smallest angle of rotation
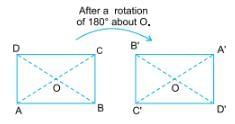
Example 4: A rectangle has rotational symmetry about its centre (the point where its diagonals meet)
Angle of rotation = 180º
∴ Order of rotational symmetry = 360º/180º = 2
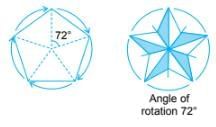
Example 5: A regular pentagon (a polygon having 5 equal sides), a design of flower design with 5 petals are the figures having rotational symmetry of order 5.
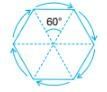
Example 6: A regular hexagon (a polygon having 6 equal sides) has rotational symmetry of order 6 and angle of rotation = 60º.
A regular octagon (a polygon having 8 equal sides) has rotational symmetry of order 8 and angle of rotation = 45º.
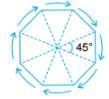
No Rotational Symmetry
- If a figure or object can come to its original position only after a rotation of 360°, it does not have any rotational symmetry.
- Example: a quadrilateral.
- Every figure can fit into itself after a rotation of 360°.
Figures with Linear Symmetry as well as Rotational Symmetry
Some figures have both types of symmetry, linear and rotational.
Consider the following examples :
- An equilateral triangle has linear symmetry having three lines of symmetry. Also, it has rotational symmetry of order 3.
- A rectangle and a rhombus both have a linear symmetry having two lines of symmetry each and rotational symmetry of order 2.
- A square has a linear symmetry having f our lines of symmetry and rotational symmetry of order 4.
All regular figures — pentagon, hexagon, octagon, nonagon, etc., have linear symmetry as well as rotational symmetry. - The letter H of the English alphabet has linear symmetry having two lines of symmetry and rotational symmetry of order 2.
Only Linear Symmetry
There are some figures which have only one line symmetry but have no rotational symmetry.
For example (a) Letters of the English alphabet A, C, D, E, M, T, U, 9, W, Y
(b) Isosceles triangle.
Only Rotational Symmetry
We have some figures that have only rotational symmetry but no linear symmetry. For example, letters of the English alphabet N, S, and Z.
Nets
If we join together six identical squares, edge to edge, we get a cube or the outside surface of the cube.

We can avoid a lot of unnecessary sticking if we join some squares together before cutting them out.
Suppose we want to make a cube out of cardboard or a piece of paper. We need a pattern giving us the shape of the cardboard or the piece of paper to make the cube.
Figure (a) below shows, the shape of the pattern of six squares. When this shape is folded along the edges, a cube is formed as shown.
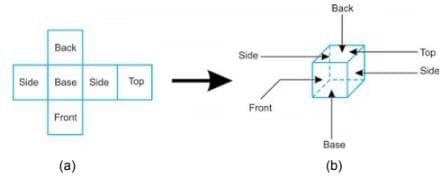
- A cross plan such as shown in Figure (a) above, which can be folded to form a cube, is called the net of the cube.
- A net of a 3D figure is a shape that can be cut out of a flat piece of paper or cardboard and folded to make the 3D shape.
- There are other arrangements of six squares that can be folded up to make a cube.
For example, a cube can also be made from the nets shown below.

However, not all arrangements of six squares will work as shown below :

It is easy to make a solid shape from a piece of paper or cardboard by first drawing a net of the faces of the solid. The net can be made up of different plane shapes (rectangles, squares, triangles).
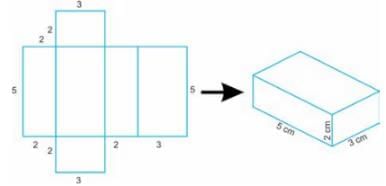
The figure below shows the net of a cuboid of dimensions 5 cm × 3 cm × 2 cm.
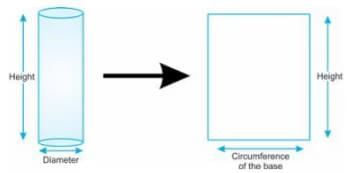
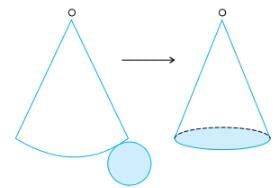
The net for a cylinder without a top and a bottom is shown. The length of the net is equal to the circumference of the cylinder.
The net of a cone has one circular base and one curved surface.
|
30 videos|112 docs|15 tests
|
FAQs on Three Dimensional Shapes Chapter Notes - Mathematics Class 6 (Maharashtra Board)
| 1. What is reflection symmetry and how is it represented in three-dimensional shapes? |  |
| 2. How do you identify planes of symmetry in three-dimensional shapes? |  |
| 3. What is rotational symmetry and how is it different from reflection symmetry? |  |
| 4. Can you provide examples of three-dimensional shapes that exhibit no rotational symmetry? |  |
| 5. What are nets in relation to three-dimensional shapes and how are they useful? |  |
|
30 videos|112 docs|15 tests
|













