Quadrilaterals Chapter Notes | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Introduction
In this chapter, we dive into the fascinating world of four-sided figures, known as quadrilaterals. The term "quadrilateral" comes from the Latin words quadri, meaning four, and latus, meaning side —together describing shapes with four sides.
What are Quadrilaterals?
A quadrilateral is a closed figure made of four straight line segments (sides), and has four vertices and four angles.
Observe the following figures.
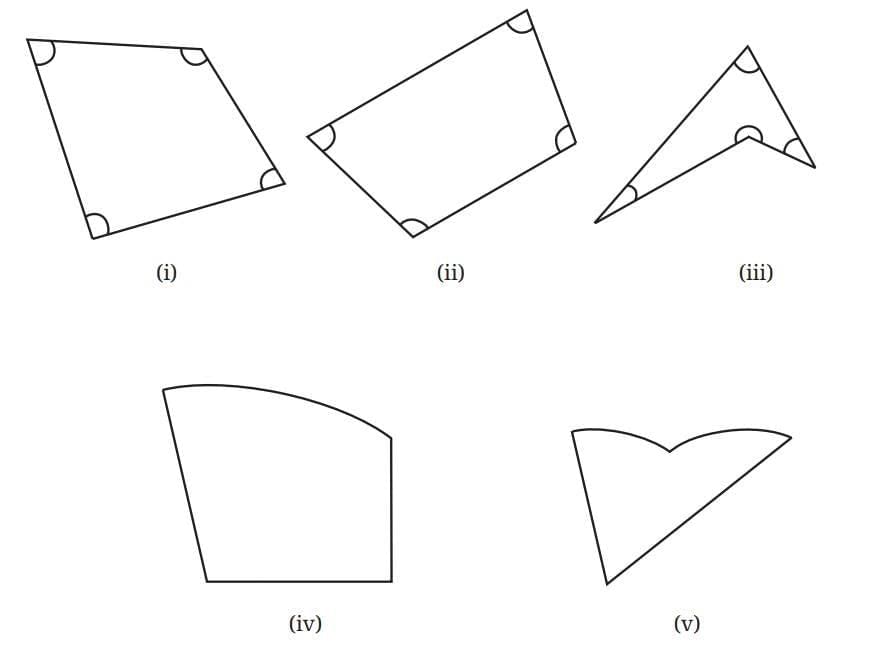
At first glance, many shapes may appear similar, but not all of them qualify as quadrilaterals. By observing a few examples, you'll learn to identify what makes a shape a quadrilateral and why certain figures don’t fit the definition.
Figs. (i), (ii), and (iii) are quadrilaterals, and the others are not
We begin our exploration with the most familiar types—rectangles and squares—before discovering the unique properties of other quadrilaterals.
Let’s unfold the shape of things—four sides at a time!
Rectangles
A rectangle is a quadrilateral where:
All angles are 90° (right angles).
Opposite sides are equal in length.
The definition precisely states the conditions a quadrilateral has to satisfy to be called a rectangle.
A Carpenter’s Problem
A carpenter wanted to make a strong rectangular frame using two thin wooden strips. She had heard that if you join two strips diagonally, from corner to corner, the frame becomes more stable and forms a perfect rectangle when tied at the ends.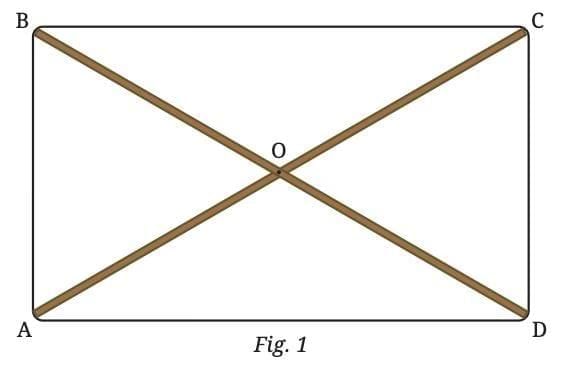
She already had one strip of wood that was 8 cm long. Now, she needed to figure out:
What should be the length of the second strip?
Where should she join them?
And, what angle should they make?
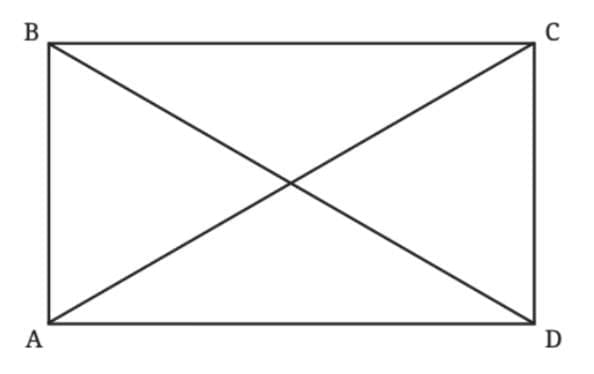
To solve this, we imagine the structure as a rectangle, with the wooden strips acting as its diagonals. Let’s name the rectangle ABCD, and let the diagonals AC and BD intersect at point O, the center of the rectangle.
Deduction 1: What is the length of the other diagonal?
Since ABCD is a rectangle, we have
AB = CD
∠BAD = ∠CDA = 90°
AD is common to both triangles.
So, ∆ ADC ≅ ∆ DAB by the SAS congruence condition.
Therefore, AC equals BD, because they are corresponding parts of two congruent triangles formed by the diagonals of the rectangle. This tells us an important geometric fact — the diagonals of a rectangle are always equal in length.
Deduction 2: What is the point of intersection of the two diagonals?
Since ABCD is a rectangle, we have
Consider triangles ∆AOB and ∆COD:
The blue angles are equal since they are vertically opposite angles.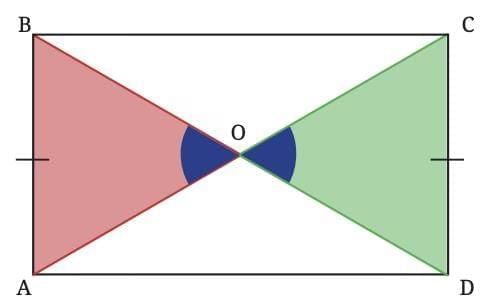 Therefore, ∠AOB = ∠COD (vertically opposite angles).
Therefore, ∠AOB = ∠COD (vertically opposite angles).
In order to show congruence, we have to deduce if∠1 and ∠2 are equal: 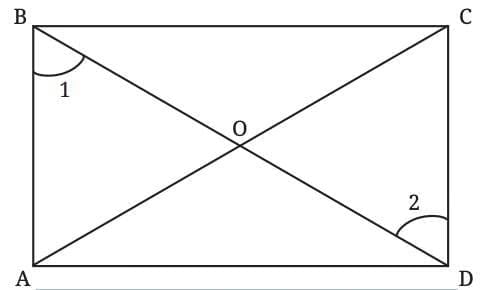
Lets deduce,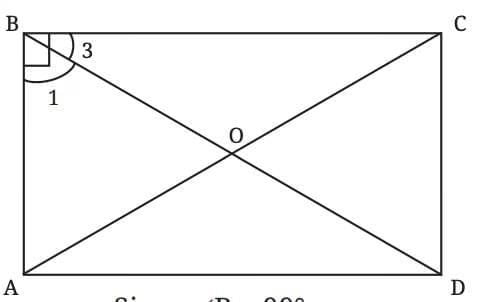 Since ∠B = 90°,
Since ∠B = 90°,
∠3 + ∠1 = 90°.
So, ∠1 = 90° - ∠3
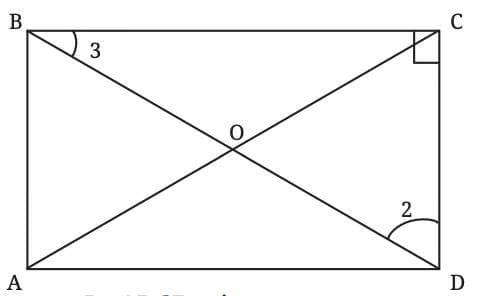
In ∆BCD,
since∠3 + ∠2 + 90 = 180,
we have ∠3 + ∠2 = 90°.
So, ∠2 = 90° - ∠3
Thus, ∠1 = ∠2 (since both equal 90° – ∠3).
Therefore In ∆AOB and ∆COD:
∠AOB = ∠COD
∠1 = ∠2
AB = CD (opposite sides).
By AAS congruence: ∆AOB ≅ ∆COD.
Thus, OA = OC, OB = OD (corresponding parts).
O is the midpoint of AC and BD, so the diagonals bisect each other.
Conclusion: The diagonals of a rectangle always intersect at their midpoints.
In geometry, when two lines cut each other at their midpoints, we say they bisect each other. The word bisect means to divide into two equal parts.
Deduction 3: What are the angles between the diagonals?
Let’s try a small experiment. Suppose we draw two diagonals:
of equal length,
that bisect each other,
but they meet at an angle of 60° instead of the usual 90°.
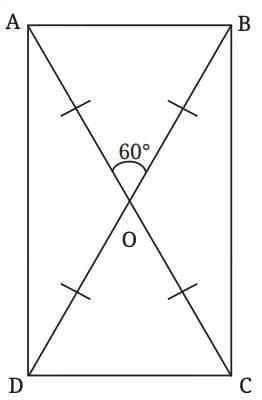
We can determine the other angles between the diagonals by using vertically opposite angles and linear pair relationships.
1. Use vertically opposite angles:
Angle AOB = 60°
Therefore, angle COD = 60° (because they are vertically opposite)
2. Use linear pairs (angles on a straight line add up to 180°):
Angle AOD = 180° - 60° = 120°
Angle BOC = 120° (again, vertically opposite to angle AOD)
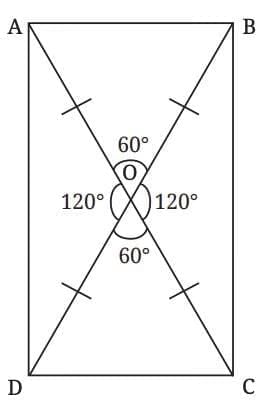
In ∆AOB, since OA = OB, the angles opposite them are equal, say a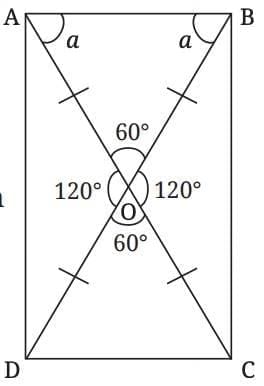
Now, let's find the value of a
In ∆AOB, we have
a + a + 60 = 180°(interior angles of a triangle).
Therefore, 2a = 120°
Thus, a = 60°
Similarly, we can find the values of all the other angles
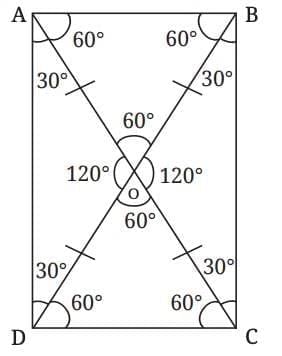
The angles add up to 90°, since 30° + 60° = 90°.
What can we say about its sides?
Proving That ABCD is a Rectangle
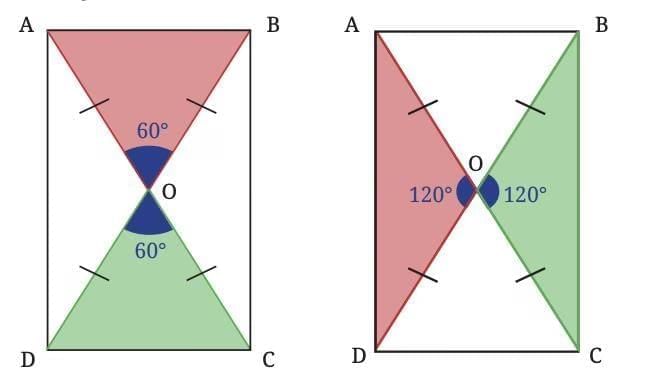
We observe that:
△AOB ≅ △COD
△AOD ≅ △COB
From this congruence, we know that the corresponding sides are equal:
AB = CD
AD = CB
Since both pairs of opposite sides are equal, and the angles are right angles (as shown earlier),
ABCD satisfies the definition of a rectangle.
Now we know how the wooden strips must be arranged to form the corners of a rectangle — they should be equal in length and joined at their midpoints.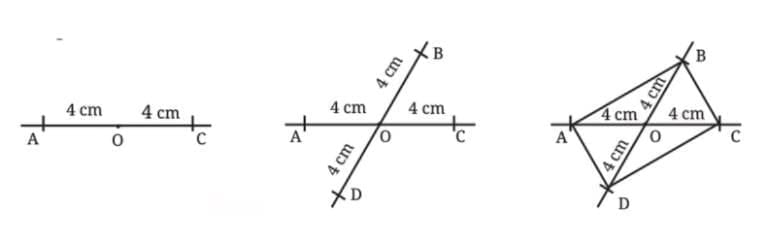
Real-Life Use of This Method
This method of using equal-length strips joined at their midpoints to form a rectangle is actually used in real-life construction.
Carpenters in Europe often use this technique to create perfectly rectangular frames.
Similarly, farmers in Mozambique (a country in Africa) apply this method while building houses, ensuring the base of the house forms a rectangle.
This simple yet effective geometric principle helps ensure accuracy and strength in construction.
The Process of Finding Properties
From earlier classes, we've learned that geometric properties—like those of parallel lines, angles, and triangles—can be discovered through logical reasoning, also called geometric deduction.
We can apply the same method to special types of quadrilaterals.
1. Deduction (Reasoning)
We use known facts and logic to prove new properties.
For example, in The Carpenter’s Problem, we deduced that the diagonals of a rectangle are equal and bisect each other.
2. Experimentation and Observation
If we struggle to deduce a property, we can try to observe it in real-life examples:
Construct a quadrilateral on paper.
Look at shapes in the real world.
Measure and observe patterns.
This method helps us form a conjecture—a statement we believe is true based on many examples, but we haven’t logically proven yet.
For example: If we draw many rectangles and observe that the diagonals always bisect each other, we might think this is always true. But without proof, we can’t be completely sure—it’s still a conjecture.
Deduction 4: What is the shape of a quadrilateral with all the angles equal to 90°?
In quadrilateral ABCD with ∠A = ∠B = ∠C = ∠D = 90°:
Join diagonal BD.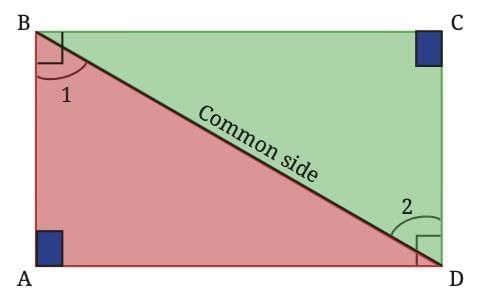
 Since ∠B = 90°,∠3 + ∠1 = 90°.
Since ∠B = 90°,∠3 + ∠1 = 90°.
∠1 = 90° - ∠3
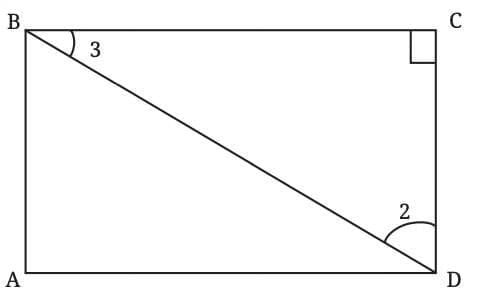 In ∆BCD, since
In ∆BCD, since
∠3 + ∠2 + 90° = 180°,
∠3 + ∠2 = 90°
∠2 = 90° - ∠3
Thus, ∠1 = ∠2. (Both are equal to 90° - ∠3)
Therefore, In ∆ BAD and ∆ DCB.
∠A = ∠C.
∠1 = ∠2.
AB = CD (opposite sides).
By AAS congruence: ∆BAD ≅ ∆DCB.
Thus, AD = CB, DC = BA (corresponding sides).
Conclusion: A quadrilateral with all angles 90° has equal opposite sides, making it a rectangle.
Note: Writing ∆BAD ≅ ∆CDB is incorrect due to mismatched vertex order.
Are the Opposite Sides of a Rectangle Parallel?
Yes, they definitely are. Let’s understand why using a transversal property from geometry.
Consider line segment AB as a transversal to the lines AD and BC.
Since ∠A and ∠B are both 90°, their sum is:
∠A + ∠B = 90° + 90° = 180°
According to the transversal property, if the sum of the interior angles on the same side of the transversal is 180°, then the lines are parallel.
Therefore, AD || BC.
Similarly, we can show:
Line AB acts as a transversal to DC and AB
Since the adjacent angles ∠A and ∠D (or ∠B and ∠C) also add up to 180°, we conclude:
AB || DC
Properties of a Rectangle
Through all the above deductions and observations, we can now summarise the key properties of a rectangle:
- Property 1: All the angles of a rectangle are 90°.
- Property 2: The opposite sides of a rectangle are equal.
- Property 3: The opposite sides of a rectangle are parallel to each other.
- Property 4: The diagonals of a rectangle are of equal length and theybisect each other.
A Special Rectangle
In the quadrilaterals shown below, we examine whether any of them are not rectangles.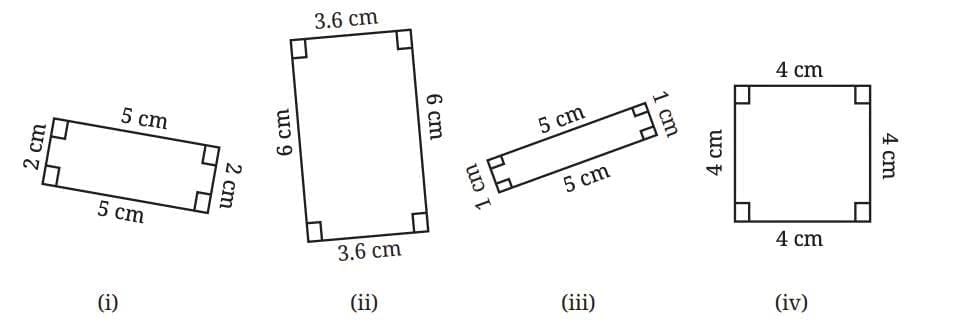
All these quadrilaterals are rectangles. Let's analyse further:
Square
A square is a quadrilateral where:
All angles = 90°
All sides are equal
This means every square satisfies the conditions to be a rectangle as well.
But the reverse is not true:
A rectangle may not have all sides equal, so not every rectangle is a square.
Real-Life Analogy
 That's because being Malayali is a part of being Indian — just like being a square is a part of being a rectangle.
That's because being Malayali is a part of being Indian — just like being a square is a part of being a rectangle.
Such relationships can be depicted easity by Venn Diagrams.
In a Venn diagram:
A set is represented as a closed curve (usually a circle or an oval). For example, the set of all squares is represented as
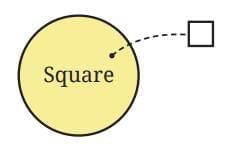
All squares are part of the rectangle family, so the set of squares is entirely inside the set of rectangles.
The Venn diagram representation of these two sets would be as follows —
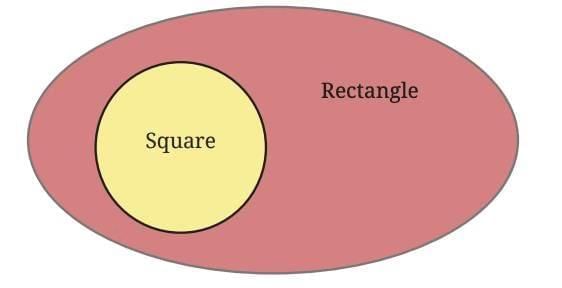
This shows:
Every square is a rectangle.
But outside the “square” circle, the rest of the rectangle set contains other rectangles that are not squares.
Carpenter’s Problem for a Square
The Carpenter’s Problem involves arranging wooden strips so that the thread joining their endpoints forms a specific quadrilateral. In this case, the target quadrilateral is a square.
A square is a special kind of rectangle, with all four sides equal.
- To achieve this an additional condition is required: Diagonals must be perpendicular to each other (intersect at 90 degrees)
Deduction 5: What should be the angle formed by the diagonals?
In square ABCD, diagonals AC and BD intersect at O.
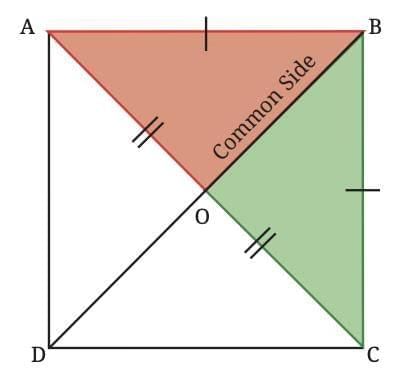
In ∆BOA and ∆BOC:
BO = BO (common).
OA = OC (diagonals bisect).
AB = BC (square sides equal).
By SSS congruence: ∆BOA ≅ ∆BOC.
∠BOA = ∠BOC (corresponding angles).
∠BOA + ∠BOC = 180° (straight line).
Thus, ∠BOA = ∠BOC = 90°.
Conclusion: Diagonals must be equal, bisect each other, and intersect at 90° to form a square.
Properties of a Square
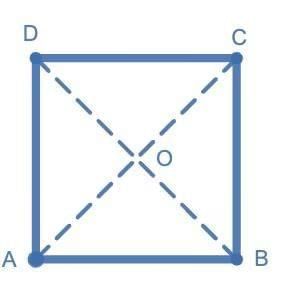
- Property 1: All sides are equal (AB = BC = CD = DA).
- Property 2: Opposite sides parallel (AB || DC, AD || BC).
- Property 3: All angles are 90°.
- Property 4: Diagonals are equal, bisect each other at 90° (AC = BD, OA = OC, OB = OD).
Note: The diagonals divide the vertex angles into two equal parts, each measuring 45°.
In ∆ADC, we have,
∠1 + ∠3 + 90 = 180
Since AD = DC, we have
∠1 = ∠3.
Thus, ∠1 = ∠3 = 45°.
In the same way, determine the measures of ∠2 and ∠4.
- Property 5: The diagonals divide the vertex angles into two equal parts, each measuring 45°.
Angles in a Quadrilateral
To analyse the sum of angles in any quadrilateral,
consider a quadrilateral SOME.
Draw a diagonal SM. We get two triangles ∆SEM and ∆SOM.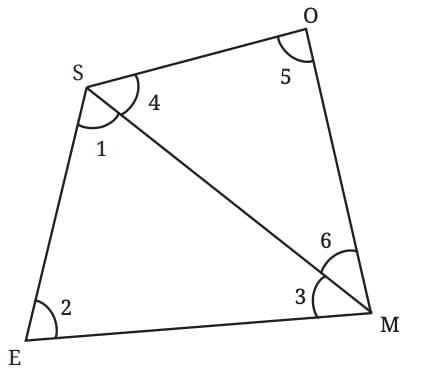
In ∆SEM:
∠1 + ∠2 + ∠3 = 180°.
In ∆SOM:
∠4 + ∠5 + ∠6 = 180°.
Adding all angles of triangles ∆SEM and ∆SOM.
(∠1 + ∠4) + (∠3 + ∠6) + ∠2 + ∠5 = 180° + 180° = 360°.
These are the quadrilateral’s angles (e.g., ∠S = ∠1 + ∠4).
Therefore, ∠S + ∠O + ∠M + ∠E = 360°.
Therefore, the sum of all angles in any quadrilateral is 360°
This shows why a quadrilateral cannot have three right angles unless the fourth angle is also a right angle.
More Quadrilaterals with Parallel Opposite Sides
Rectangles and squares are special quadrilaterals where:
- Opposite sides are parallel.
- All angles are right angles (90°).
But can a quadrilateral have opposite sides parallel without being a rectangle?
Let’s explore:
Try drawing two pairs of parallel lines that do not intersect at 90° angles.
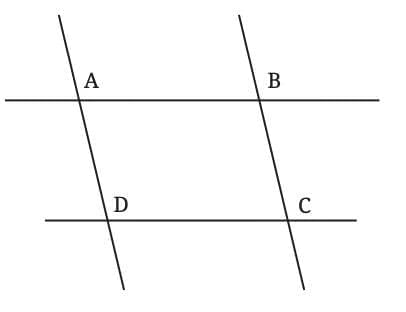
Observation:
In the quadrilateral ABCD, we find:
AB || CD and AD || BC.
But none of the angles are 90°.
Hence, it is not a rectangle.
Therefore, there is a broader category of quadrilaterals where the opposite sides are parallel. These types of quadrilaterals are known as parallelograms.
Is a Rectangle a Parallelogram?
Yes, a rectangle is indeed a parallelogram. This is because a rectangle has both pairs of opposite sides parallel, which matches the basic definition of a parallelogram.
However, a rectangle has an additional property — all its angles are right angles (90°). This makes a rectangle a special type of parallelogram.
So, we can say:
Every rectangle is a parallelogram, but not every parallelogram is a rectangle.
We can represent this relationship using a Venn diagram, where the set of all rectangles is shown as a subset within the larger set of all parallelograms.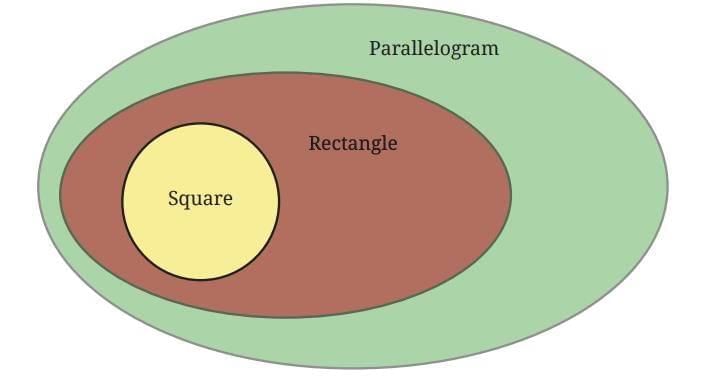
To explore further, let's construct and study a parallelogram to understand the relationship between its sides and angles.
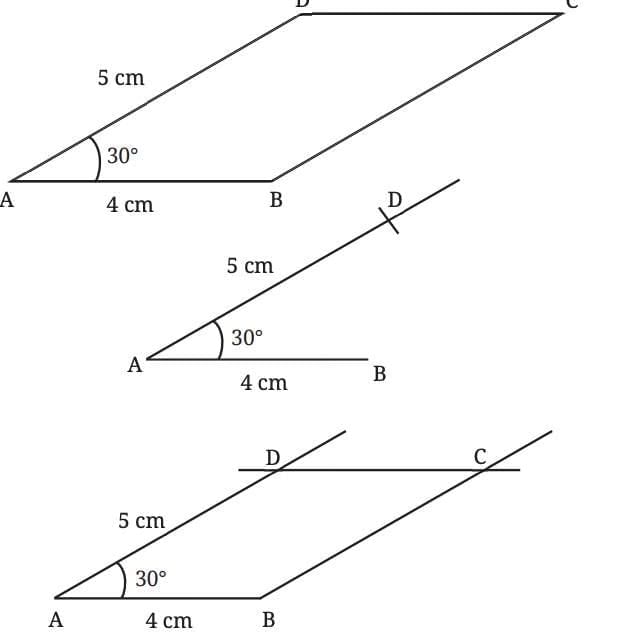
Example: Draw a parallelogram with adjacent sides of lengths 4 cm and 5 cm, and an angle of 30° between them.
Solution:
Step 1: Draw the base
Use a ruler to draw line segment AB = 4 cm.
Step 2: Construct angle 30° at point A
At point A, use a protractor to draw a 30° angle.
Along this angle, use a ruler to draw line segment AD = 5 cm.
Step 3: Draw line parallel to AB through point D
Using a set-square or compass, draw a line through point D that is parallel to AB.
Step 4: Draw line parallel to AD through point B
Again using a set-square or compass, draw a line through point B that is parallel to AD.
Step 5: Mark the intersection point as C
The point where the lines from Steps 3 and 4 intersect is point C.
Now, join points C to B and C to D.
Deduction 6— What can we say about the angles of a parallelogram?
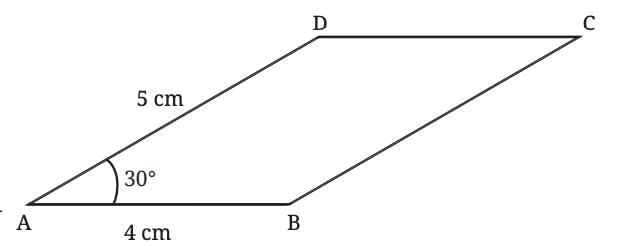 In parallelogram ABCD, we know that AB is parallel to CD, and AD acts as a transversal.
In parallelogram ABCD, we know that AB is parallel to CD, and AD acts as a transversal.
So, the interior angles on the same side of the transversal (∠A and ∠D) must add up to 180°:
∠A + ∠D = 180°
If ∠A = 30°, then
∠D = 180° – 30° = 150°
Similarly, since AD is parallel to BC, and lines AB and CD act as transversals, we get:
∠A + ∠B = 180°
∠C + ∠D = 180°
Using this logic, we find:
∠B = 150° and ∠C = 30°
So, in this parallelogram:
Each pair of adjacent angles adds up to 180°:
∠A + ∠B = ∠A + ∠D = ∠C + ∠D = ∠B + ∠C = 180°
Each pair of opposite angles is equal:
∠A = ∠C and ∠B = ∠D
This pattern holds true in all parallelograms. Let’s prove this generally: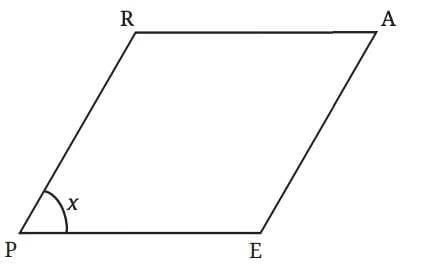
Suppose one angle is x.
Then, the angle opposite to it must also be x, because:
Since ∠P + ∠R = 180°,
∠R = 180° – x
And ∠A + ∠R = 180°,
∠A = 180° – (180° – x) = x
So:
∠P = ∠A = x
∠R = ∠E = 180° – x
Deduction 7: What can we say about the sides of a parallelogram?
At first glance, it seems that the opposite sides of a parallelogram are equal. But can we prove it logically, perhaps using congruence of triangles?
Let’s consider triangles ∆ABD and ∆CDB within parallelogram ABCD
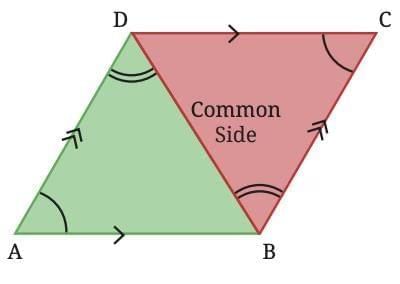
In parallelogram ABCD:
∠ABD = ∠CDB (They are opposite angles of the parallelogram — so they are equal.)
Also, since AD || BC and BD is a transversal,
∠ADB = ∠CBD (These are alternate interior angles, and hence equal.)
The side BD is common to both triangles ∆ABD and ∆CDB.
Using the AAS (Angle–Angle–Side) criterion: ∆ ABD ≅ ∆ CDB
Therefore, the corresponding sides of these triangles are equal:
AD = BC
AB = CD
Thus, opposite sides of a parallelogram are always equal.
Properties of Parallelogram
- Property 1: The opposite sides of a parallelogram are equal.
- Property 2: The opposite sides of a parallelogram are parallel.
- Property 3: In a parallelogram, the adjacent angles add up to 180°, and the opposite angles are equal.
Deduction 8— What is the point of intersection of the two diagonals in a parallelogram?
In parallelogram EASY, diagonals AE and YS intersect at O.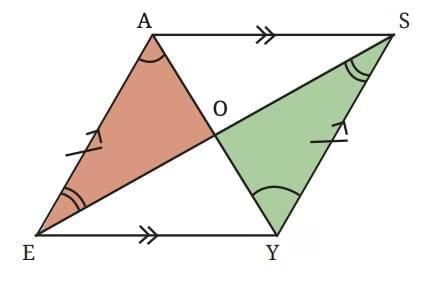
In ∆AOE and ∆YOS:
AE = YS (opposite sides).
∠EAO = ∠OYS, (alternate angles, AE || YS).
∠AEO = ∠YOS (alternate angles, AE || YS).
By ASA congruence: ∆AOE ≅ ∆YOS.
Therefore, corresponding parts of the triangles are equal:
OA = OY
OE = OS
Thus, the point O, where the diagonals intersect, is the midpoint of both diagonals. Hence, the diagonals of a parallelogram bisect each other.
- Property 4: The diagonals of a parallelogram bisect each other.
Quadrilaterals with Equal Side Lengths
Squares are not the only quadrilaterals with equal side lengths.
Let’s investigate this through a construction.
Start by drawing two equal sides, AD and AB, but not at a right angle to each other.
Use a compass to measure the length of AB, then place the compass point on the other arm and draw an arc and mark point– D at the same distance.
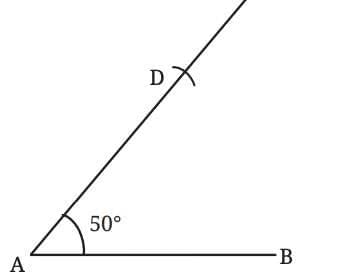
Keeping this length fixed, draw arcs from points B and D. Mark their point of intersection as C.
Join D to C and B to C

You’ve now formed a quadrilateral ABCD where all four sides are equal.
In this construction, ∠BAD is 50°, but you could choose any angle less than 180° to create a different quadrilateral with all sides equal.
Rhombus
A quadrilateral in which all the sides have the same length is a rhombus.
Deduction 9— What can we say about the angles in a rhombus?
Let’s consider a rhombus named GAME.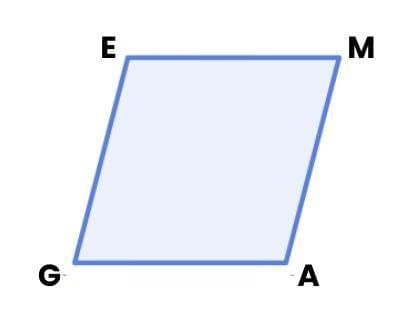
In triangle ∆GAE, since sides GE and GA are equal, we get:
a = d.
Similarly, in triangle ∆MAE, ME = MA, so:
b = c.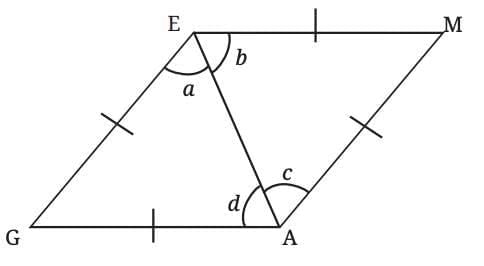
In triangles GAE and MAE:
GA = MA (Sides of rhombus — all sides are equal)
AE = AE (Common side)
∠GAE = ∠MAE (Diagonal GE = ME, and diagonal GM bisects ∠G and ∠M, so these angles are equal)
Therefore, ∆GAE ≅ ∆MAE by SAS (Side-Angle-Side) Congruence Rule
Thus, a = b = c = d, and ∠G = ∠M, (Corresponding angles of congruent triangles)
These properties apply to any rhombus.
Now, let’s apply them to the rhombus ABCD that we constructed earlier. Let the four angles formed at the intersection of the diagonals be all equal, each marked a.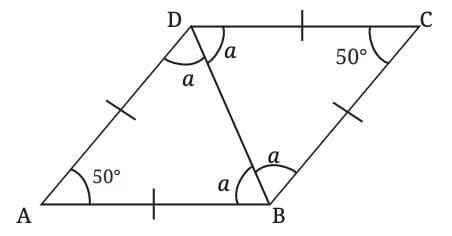
In triangle ∆ADB, the angle sum is:
a + a + 50° = 180°,
which gives:
a = 65°.
Hence, the angles of the rhombus ABCD are:
50°, 130°, 50°, and 130°.
This confirms that opposite angles in a rhombus are equal.
Another Way: Interestingly, another way to find the remaining angles of the rhombus is to use the fact that the diagonals of a rhombus bisect each other at equal angles.
- Consider the lines EM and GA and its transversal AE. Since the alternate angles are equal, EM||GA.
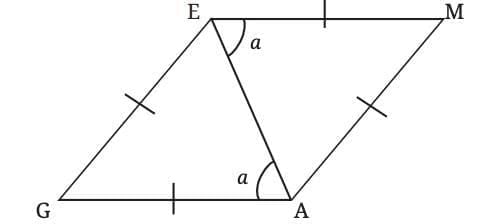
- Similarly, consider the lines GE and AM and its transversal AE. Since the alternate angles are equal, GE||AM.
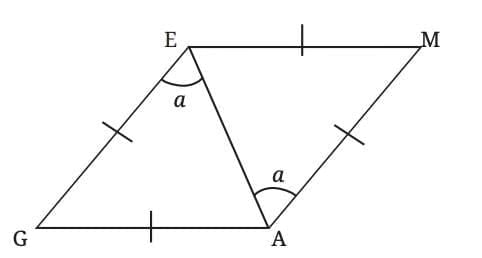
Since opposite sides are parallel, GAME is a parallelogram.
This means every rhombus is also a parallelogram, and all properties of parallelograms apply to rhombuses.
Therefore:
Opposite angles are equal
Adjacent angles add up to 180°
These can be verified using the same reasoning as in Deduction 6.
Example (Rhombus ABCD):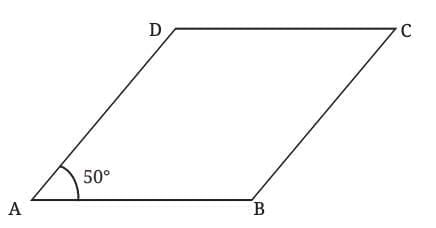
If ∠A = ∠C = 50°,
then ∠D = ∠B = 180° – 50° = 130°
Venn Diagram Showing Relationship Between Rectangle, Rhombus, Parallelogram and Square
We know that a square is a rectangle, because it has all the properties of a rectangle — opposite sides are equal and all angles are 90°.
Since the opposite sides are also parallel, a square is a parallelogram.
Furthermore, as all sides are of equal length, a square is also a rhombus.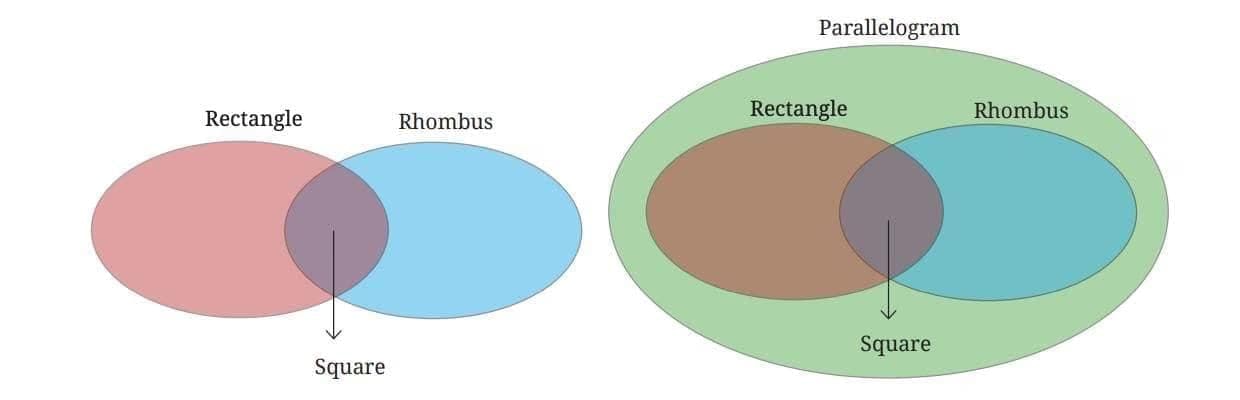
Let us list the properties of a rhombus.
- Property 1: All the sides of a rhombus are equal to each other.
- Property 2: The opposite sides of a rhombus are parallel to each other.
- Property 3: In a rhombus, the adjacent angles add up to 180°, and the opposite angles are equal.
- Property 4: The diagonals of a rhombus bisect each other.
- Property 5: The diagonals of a rhombus bisect its angles.
|
13 videos|105 docs
|
FAQs on Quadrilaterals Chapter Notes - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are the main properties of a rectangle? |  |
| 2. How can we solve a carpenter's problem involving rectangles? |  |
| 3. What distinguishes a square from a rectangle? |  |
| 4. What are the properties of a parallelogram? |  |
| 5. How is the carpenter's problem applied to squares specifically? |  |