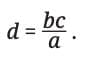Proportional Reasoning-1 Chapter Notes | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Introduction
In our daily life, we often change the size and orientation of digital images to suit our needs.
Some images look similar after resizing, while others look distorted.
Why does this happen? Let us observe.
Observing Similarity in Change
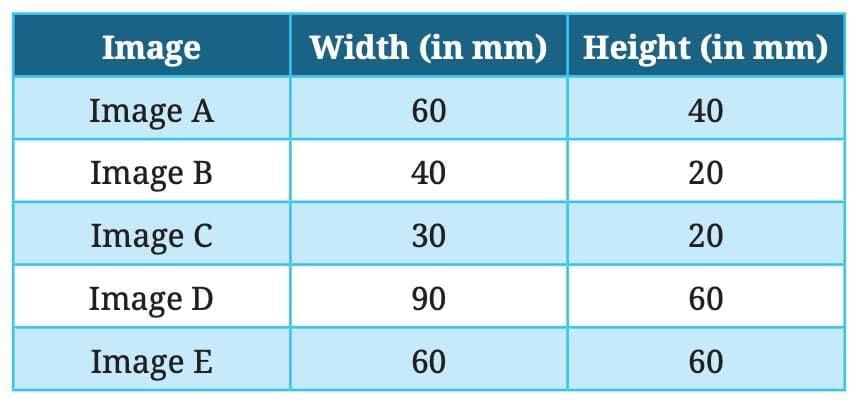
Suppose we have five images A, B, C, D, and E.
Images A, C, and D look similar, even though their sizes are different.
Images B and E look different. [B is stretched (elongated) and E is squished (fatter)]
Let us check the measurements.
Comparing Images
Case 1: Image A vs. Image C
Width of C = 30 (half of A’s width).
Height of C = 20 (half of A’s height).
Both width and height are changed by the same factor (½).
Therefore, Image C looks similar to Image A.
Case 2: Image A vs. Image B
Width of B = 40 (20 less than A’s width).
Height of B = 20 (20 less than A’s height).
Even though both decreased by 20, the factors are not the same.
Width factor = 40 ÷ 60 = 2/3
Height factor = 20 ÷ 40 = ½
Since the width and height changed by different factors,
Image B looks distorted compared to Image A.
Case 3: Image A vs. Image D
Width of D = 90, Height = 60.
Compared to A:
Width factor = 90 ÷ 60 = 3/2
Height factor = 60 ÷ 40 = 3/2
Both width and height changed by the same factor (3/2).
So, Image D looks similar to Image A.
Case 4: Image A vs. Image E
Width of E = 60 (same as A), Height of E = 60 (greater than A).
Width factor = 60 ÷ 60 = 1
Height factor = 60 ÷ 40 = 3/2
Since factors are different, Image E looks different.
Conclusion
When both width and height change by the same multiplication factor, the image looks similar. This is called a Proportional Change.
- Proportional change = shape stays the same
- Non-proportional change = shape looks distorted
Ratios
We saw earlier that images A, C, and D looked similar because their width and height changed in the same way. Now, let us use ratios to understand this better.
What is a Ratio?
A ratio is a way to compare two quantities of the same kind.
It shows how many times one quantity contains another.
A ratio is written in the form a : b, which is read as "a is to b".
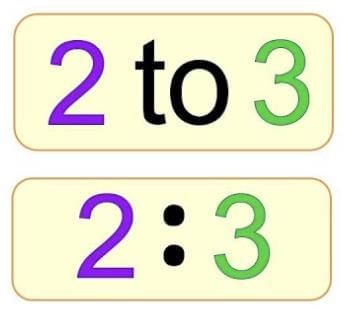
Example:
- The ratio of width to height of Image A is 60 : 40.
Here, 60 and 40 are called the terms of the ratio. - The ratio of width to height of Image C is 30 : 20.
The ratio of width to height of Image D is 90 : 60.
General rule:
In a ratio a : b, we can say that for every a units of the first quantity, there are b units of the second quantity.
Ratios in their Simplest Form
Reducing Ratios
Ratios can be reduced to their simplest form by dividing both terms by their Highest Common Factor (HCF).
This makes comparison easier.
Example : Lets assume Ratio = 60 : 40
HCF of 60 and 40 = 20
Divide both terms by 20 → (60 ÷ 20) : (40 ÷ 20) = 3 : 2
Simplest form of Ratio = 3 : 2
Following our previous example:

For Image A, the ratio of width to height is 60 : 40.
- HCF of 60 and 40 is 20.
- Divide both terms by 20: 60 ÷ 20 = 3, 40 ÷ 20 = 2.
- Simplest form: 3 : 2.
For Image D, the ratio is 90 : 60.
- HCF of 90 and 60 is 30.
- Divide both terms by 30: 90 ÷ 30 = 3, 60 ÷ 30 = 2.
- Simplest form: 3 : 2.
Since the simplest forms of the ratios for Images A and D are both 3 : 2, they are proportional.
For Image B, the ratio is 40 : 20.
- HCF of 40 and 20 is 20.
- Divide both terms by 20: 40 ÷ 20 = 2, 20 ÷ 20 = 1.
- Simplest form: 2 : 1.
For Image E, the ratio is 60 : 60.
- HCF of 60 and 60 is 60.
- Divide both terms by 60: 60 ÷ 60 = 1, 60 ÷ 60 = 1.
- Simplest form: 1 : 1.
Ratios as Proportional Relationships
A proportional ratio is when two ratios express the same relationship between numbers.
In other words, if you can turn one ratio into the other by multiplying or dividing both parts by the same number, the ratios are proportional.
Example:
60 : 40 → ÷20 (HCF) → 3 : 2
90 : 60 → ÷30 (HCF) → 3 : 2
40 : 20 → ÷20 (HCF) → 2 : 1 (not proportional to 3 : 2).
60 : 60 → ÷60 (HCF) → 1 : 1 (not proportional to 3 : 2).
General Rule
When two ratios are the same in their simplest forms, they are said to be in proportion.
We use the symbol ‘::’ to show proportion.Example:
If a : b = c : d, then we write
a : b :: c : dThis means a : b and c : d are proportional.
Problem Solving with Proportional Reasoning
Example 1: Are the ratios 3 : 4 and 72 : 96 proportional?
 View Answer
View Answer 
Solution: Step 1: The ratio 3 : 4 is already in its simplest form.
Step 2: Simplify 72 : 96.
Find the HCF of 72 and 96 = 24.
Divide both terms by 24 → (72 ÷ 24) : (96 ÷ 24) = 3 : 4
Conclusion: Since both ratios reduce to the same simplest form (3 : 4), the two ratios are proportional.
Example 2: Kesang wanted to make lemonade for a celebration. She made 6 glasses of lemonade in a vessel and added 10 spoons of sugar to the drink. Her father expected more people to join the celebration. So he asked her to make 18 more glasses of lemonade.
 View Answer
View Answer 
Given:
Glasses : Sugar = 6 : 10
According to question we write:
6 : 10 :: 18 : ?
Finding the factor of change.
The number of glasses increases from 6 to 18.
Factor of change = 18 ÷ 6 = 3.
Apply the same factor to sugar.
Sugar = 10 × 3 = 30 spoons.
Conclusion: To make 18 more glasses of lemonade, Kesang should add 30 spoons of sugar.
Trairasika - The Rule of Three
The Rule of Three is a method used in proportional reasoning.
It helps us solve problems involving four quantities, where three are known, and the fourth has to be found.
The relationship is set up in the form of a proportion.
Let us understand this using an example
Example: For the mid-day meal in a school with 120 students, the cook usually makes 15 kg of rice. On a rainy day, only 80 students came to school. How many kilograms of rice should the cook make so that the food is not wasted
In our rainy-day school lunch example:
- Normal day: 120 students → 15 kg rice
- Rainy day: 80 students → ? kg rice
The ratio of students to rice must remain the same.
So,
120 : 15 :: 80 : ?
Factor of change is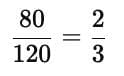
This means the number of students has been reduced to two-thirds of the original.
We can apply same factor change to rice
- So, rice needed =
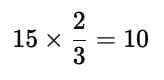
Therefore, the cook should prepare 10 kg of rice.
Lets Explore The Algebra Behind It
If two ratios are proportional:
a : b :: c : d
Then:
c is a multiple of a by some factor f
→ c = f × a ...(i)d is a multiple of b by the same factor f
→ d = f × b ...(ii)From (i) and (ii)
f = c / a
f = d / b
So, c / a = d / b
Multiplying both sides by ab, we get,
bc = ad or ad = bc
Thus, when a : b :: c : d, then ad = bc. This is known as cross multiplication of terms.
Since ad = bc, we can show that
This is called the Rule of Three or Trairasika — when three values are known and we find the fourth that keeps the proportion.
Ancient Wisdom: Āryabhaṭa’s Method
In ancient India, great mathematicians like Āryabhaṭa (born 199 CE) studied problems of proportionality.
These were called Rule of Three problems.
They involved three known numbers and finding a fourth unknown number.
The Terminology Used
Pramāṇa → The measure (this is the first term ‘a’)
Phala → The fruit or result (this is the second term ‘b’)
Ichchhā → The requisition or desired measure (this is the third term ‘c’)
Ichchhāphala → The yield or required result (this is the fourth term ‘d’)
So, the proportion can be written as:
Pramāṇa : Phala :: Ichchhā : Ichchhāphala
Āryabhaṭa gave a simple method:
“Multiply the Phala (result) by the Ichchhā (requisition) and divide by the Pramāṇa (measure).”
Mathematically,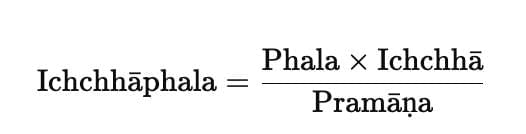
In ancient India, this was known as Trairasika. Āryabhaṭa (199 CE) explained it like this:
Rule of Three problems.
There were 3 numbers given:
- Pramāṇa = measure (a)
- Phala = known outcome (b)
- Ichchhā = desired measure (c)
To find Ichchhāphala = desired outcome (d), Āryabhaṭa says, “Multiply the phala by the ichchhā and divide the resulting product by the pramāṇa.”
In other words, Āryabhaṭa says,
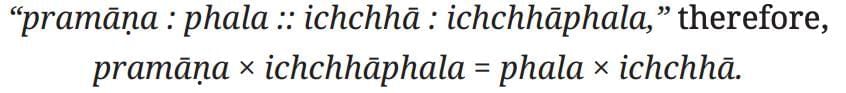
Then, according to him:
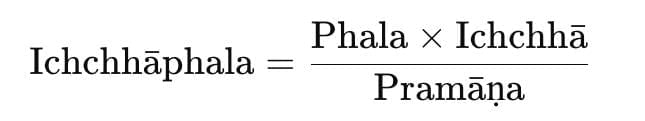
Which is the same as our modern formula!
If a : b :: c : d then ad = bc.
Therefore, d = (b × c) / a.
This shows how ancient Indians were already using advanced proportional reasoning to solve real-world and complex mathematical problems.
Sharing, but Not Equally!
Let us begin with an activity:
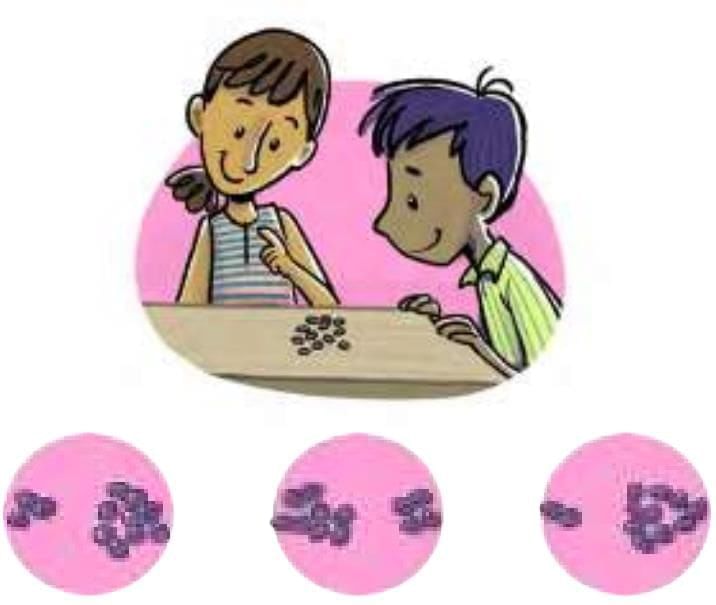
Take 12 objects (coins, seeds, pebbles). Now, form a pair and try sharing them in different ways.
If both of you get the same number:
You each get 6 counters
Ratio = 6 : 6 = 1 : 1 (simplest form)
This implies that Equal share = Equal ratioIf you both get the following number:
Your partner gets 5 counters
You get 7 counters
This implies that Partner: You = 5 : 7Now, if you want to divide 12 counters in the ratio 3 : 1.
Let’s build this step-by-step:
First, your partner gets 3, you get 1 → 4 counters used
Repeat:
Next 3 for partner, 1 for you → 8 used
Final 3 for partner, 1 for you → 12 used
So:
Partner = 3 + 3 + 3 = 9 counters
You = 1 + 1 + 1 = 3 counters
Total = 12
Ratio = 9 : 3 = 3 : 1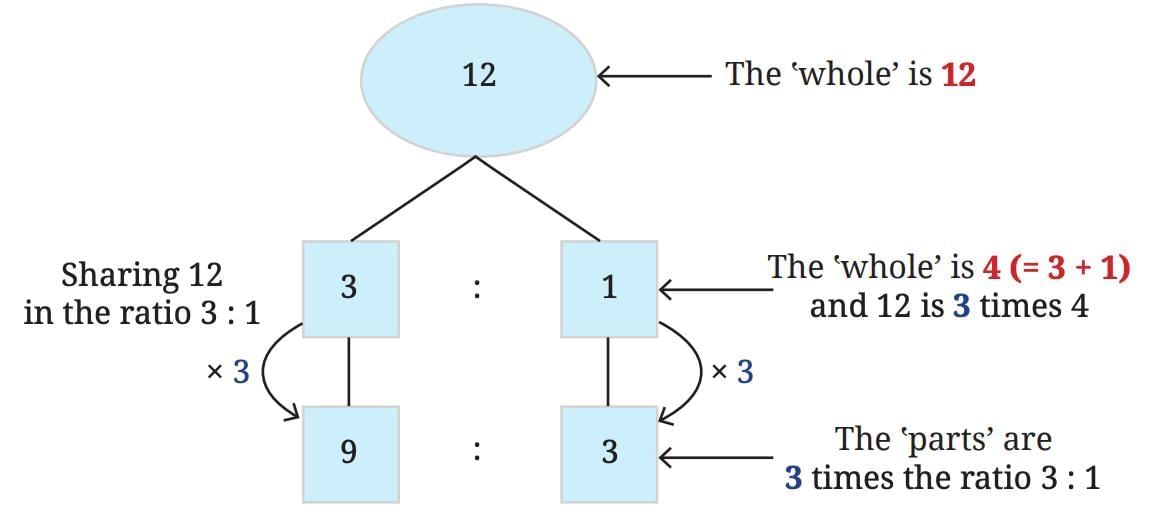
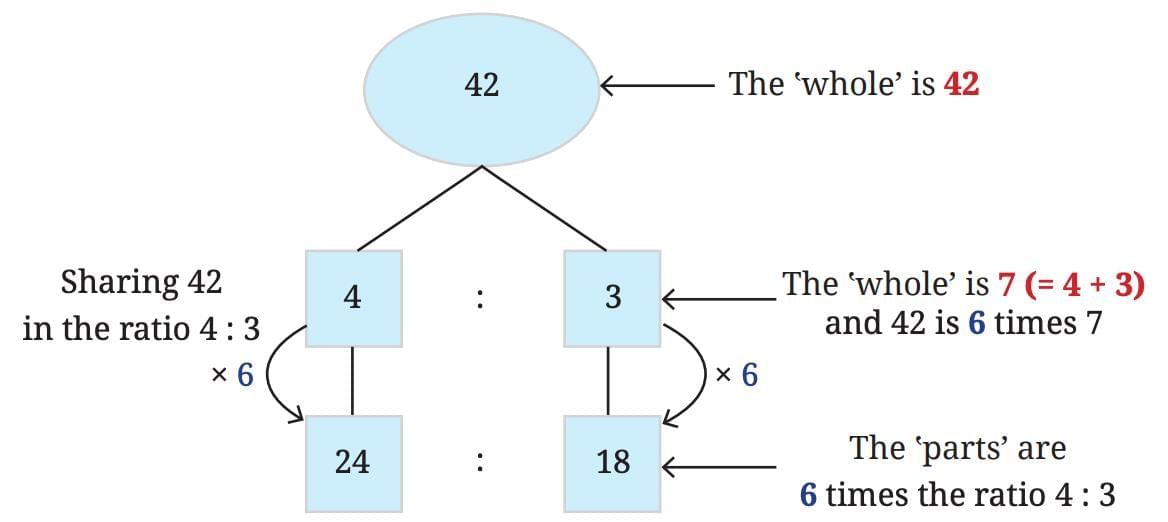
What if you had to share 42 counters in the ratio 4 : 3?
Repeating the steps will take too long! Let’s use a quicker method.
To divide 42 in the ratio 4 : 3:
Add the parts:
parts in totalFind the size of one part:
Now multiply:
Partner gets:
You get:
So, 42 shared in 4 : 3 becomes 24 : 18
General Rule for Sharing
To divide a quantity in the ratio
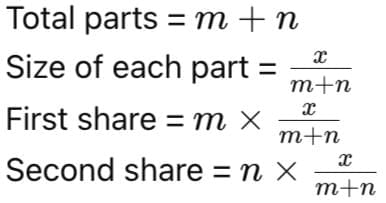
Hence, 
This method gives parts in exact proportion to the ratio.
Let’s Try One!
Divide 60 in the ratio 2 : 3
Total parts = = 5
Each part = =12
Shares:
First =
Second =
So, 60 is split as 24 : 36
Unit Conversions
- When solving problems involving proportionality, it is often necessary to convert units to ensure consistency across measurements.
- Using the same units for all quantities in a ratio or proportion ensures accurate comparisons.
Key Unit Conversions
(a) Length:
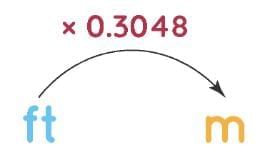
- 1 metre = 3.281 feet
(b) Area:
- 1 square metre = 10.764 square feet
- 1 acre = 43,560 square feet
- 1 hectare = 10,000 square metres
- 1 hectare = 2.471 acres
(c) Volume:
- 1 millilitre (mL) = 1 cubic centimetre (cc)

- 1 litre = 1,000 mL or 1,000 cc
(d) Temperature:
Conversion between Fahrenheit and Celsius:
- Fahrenheit = (9/5 × Celsius) + 32
- Celsius = 5/9 × (Fahrenheit - 32)

Application in Proportions
- When comparing ratios (e.g., length of a wall to cement bags), ensure all measurements are in the same units before simplifying or checking proportionality.
- Example: If one wall’s length is given in metres and another in feet, convert both to the same unit (using 1 metre = 3.281 feet) to compare ratios accurately.
Key Points to Remember
- Convert units to the same system before comparing ratios or solving proportion problems.
- Use the provided conversion factors for length, area, volume, and temperature to ensure accurate calculations.
- Temperature conversions require specific formulas, unlike direct multiplication for other units.
|
13 videos|91 docs
|
FAQs on Proportional Reasoning-1 Chapter Notes - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is a ratio and how is it used in mathematics? |  |
| 2. How do you simplify a ratio to its simplest form? |  |
| 3. What is the Rule of Three in proportional reasoning? |  |
| 4. Can you provide an example of using ratios in real-life situations? |  |
| 5. How do ratios relate to fractions and percentages? |  |