Power Play Chapter Notes | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
| Table of contents |

|
| Experiencing the Power Play ... |

|
| Exponential Notation and Operations |

|
| The Other Side of Powers |

|
| Powers of 10 |

|
| Did You Ever Wonder? |

|
| A Pinch of History |

|
Experiencing the Power Play ...
An Impossible Venture!
How many times can you fold it over and over?
 Estu and Roxie
Estu and Roxie
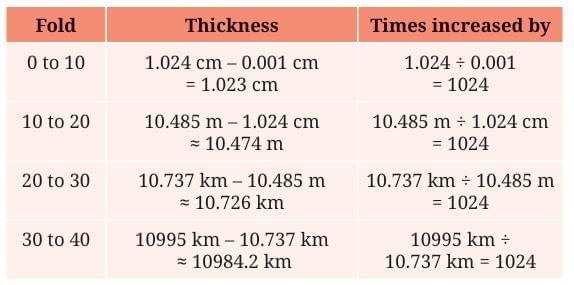
Let's find out how thick a paper would be after 46 folds, assuming its starting thickness is 0.001 cm.

What happens when you fold a paper many times?
Every time you fold a paper, its thickness doubles.
That means:
After 1 fold → thickness becomes 2 times
After 2 folds → thickness becomes 4 times (2 × 2)
After 3 folds → thickness becomes 8 times (2 × 2 × 2)

You can see that each time, the thickness doubles.
What happens after 10 folds?
The thickness becomes 1024 times more than before.
This is because:
So, every 10 folds increase the thickness by 1024 times (That is 2 multiplied by itself 10 times), no matter where you start from.
Exponential Notation and Operations
Folding a Paper – Understanding the Pattern
The starting thickness of a paper is 0.001 cm.
When we fold it once, the thickness becomes:
0.001 cm × 2 = 0.002 cmWhen we fold it twice:
0.001 cm × 2 × 2 = 0.004 cm
This is also written as:0.001 cm × 2²When folded three times:
0.001 cm × 2 × 2 × 2 = 0.008 cm
This is also written as:0.001 cm × 2³When folded four times:
0.001 cm × 2 × 2 × 2 × 2 = 0.016 cm
Or:0.001 cm × 2⁴
So, every time you fold the paper, you multiply the thickness by 2.
After 7 folds, the thickness becomes:
0.001 cm × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 0.001 cm × 2⁷ = 0.128 cm
This pattern shows how the thickness grows very fast using powers of 2.
What is Exponential Notation?
Exponential notation is a shorthand way of writing repeated multiplication of the same number.
Examples:
n × n = n²→ read as "n squared" or "n raised to the power 2"n × n × n = n³→ read as "n cubed" or "n raised to the power 3"n × n × n × n = n⁴→ read as "n raised to the power 4"n × n × n × n × n × n × n = n⁷→ "n raised to the power 7"
In general:
nᵃmeans you are multiplyingnby itselfatimes.
Examples of Exponential Form
5⁴ = 5 × 5 × 5 × 5 = 625
- This is called the exponential form of 625.
- Here, 5 is the base, and 4 is the exponent or power.
It is read as:
“5 raised to the power 4”
or “5 to the power 4”
or “5 power 4”
or “4th power of 5”
Here, 4 is the exponent/power, and 5 is the base.
2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 210 = 1024
Remember 210? This shows that after 10 folds, the paper becomes 1024 times thicker.
Lets see some more examples:
4 × 4 × 4 = 4³ = 64
This is read as "4 raised to the power 3" or "4 cubed".
Lets take cube of -4.
(–4) × (–4) × (–4) = (–4)³ = –64
The cube is negative because multiplying three negative numbers gives a negative result.
Using Letters (Algebra) in Exponential Form
When letters are multiplied, we can also use exponents:
a × a × a × b × b
=a³ × b²
This is read as "a cubed times b squared"a × a × b × b × b × b
=a² × b⁴
This is read as "a squared times b raised to the power 4"
So, each letter is multiplied by itself the number of times shown in the exponent.
It’s important not to confuse addition with exponents:
4 + 4 + 4 = 3 × 4 = 12→ This is repeated addition4 × 4 × 4 = 4³ = 64→ This is repeated multiplication
Express the number 32400 as a product of its prime factors and represent the prime factors in their exponential form.
Step 1: Prime Factorisation
We break 32400 into its prime factors:
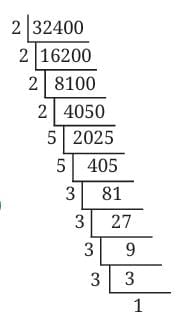
32400 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5
So we have:
- Four 2s
- Four 3s
- Two 5s
Step 2: Writing in Exponential Form
Now we group the same prime numbers and use exponents to show how many times each is used:
- 2 × 2 × 2 × 2 = 2⁴
- 3 × 3 × 3 × 3 = 3⁴
- 5 × 5 = 5²
So, in exponential form:
32400 = 2⁴ × 3⁴ × 5²
The Stones that Shine ...

Three daughters with curious eyes,
Each got three baskets — a kingly prize.
Each basket had three silver keys,
Each opens three big rooms with ease.
Each room had tables — one, two, three, With three bright necklaces on each, you see. Each necklace had three diamonds so fine…
Can you count these stones that shine?
Hint: Find out the number of baskets and rooms.
How many rooms were there altogether?
Lets see by this diagram:
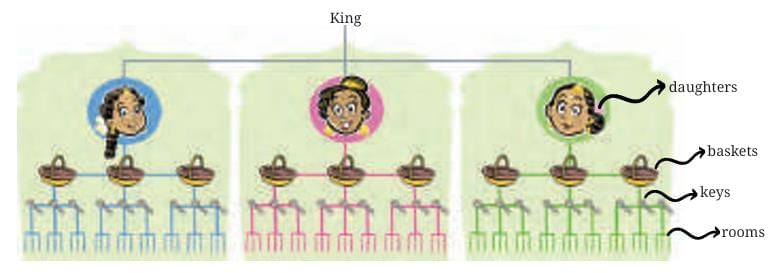
From the diagram, the number of rooms is 34. This can be computed by repeatedly multiplying 3 by itself,
3 × 3 = 9.
9 × 3 = 27.
27 × 3 = 81.
81 × 3 = 243.
How many diamonds were there in total? Can we find out by just one multiplication using the products above?
total diamonds = 3 × 3 × 3 × 3 × 3 × 3 × 3 = 3⁷ = 2187
Instead of writing 3 × 3 × 3 × 3 × 3 × 3 × 3, we write:
3⁷ (read as "3 to the power 7")
3⁷ = (3 × 3 × 3 × 3) × (3 × 3 × 3)
We already calculated that:
3⁴ = 81
And using above calculations, we also know that 3³ = 27.
So, we can just multiply 3⁴ by 3³
Then:
3⁴ × 3³ = 81 × 27 = 2187
This is a shortcut using exponents.
Rules of Exponents
Multiplying same bases
If the base is the same, just add the powers:
p⁴ × p⁶ = p¹⁰
because (p × p × p × p) × (p × p × p × p × p × p) = p¹⁰
General Rule:
nᵃ × nᵇ = nᵃ⁺ᵇ
General Rule for Powers of Powers
(nᵃ)ᵇ = (n)ᵃ×ᵇ , where a and b are counting numbers.
This means:
- (2⁵)² = 2⁵ × 2⁵ = 2¹⁰
- (3²)⁴ = 3⁸
- (nᵃ)ᵇ = (nᵇ)ᵃ = nᵃ×ᵇ
Magical Pond
Q. In the middle of a beautiful, magical pond lies a bright pink lotus. The number of lotuses doubles every day in this pond. After 30 days, the pond is completely covered with lotuses. On which day was the pond half full?
Answer:
- The number of lotuses doubles daily.
- On day 30, the pond is fully covered.
- Since the lotuses double every day, the day before (day 29), the pond must have been half full.
- This is because doubling the lotuses from day 29 to day 30 makes the pond fully covered.
The pond was half full on day 29.
Q. Write the number of lotuses (in exponential form) when the pond was —
(i) fully covered (ii) half covered
Answer:
Let’s assume we start with 1 lotus on day 1.
The number of lotuses doubles each day, so:
- On day 1: 1 lotus
- On day 2: 1 × 2 = 2 lotuses
- On day 3: 2 × 2 = 4 lotuses
- On day 4: 4 × 2 = 8 lotuses
- And so on.
This pattern shows the number of lotuses on day “n” is 2(n-1).
For day 30 (fully covered):
- Number of lotuses = 2(30-1) = 229.
For day 29 (half covered):
- Number of lotuses = 2(29-1) = 228.
- (i) Fully covered (day 30): 229 lotuses
- (ii) Half covered (day 29): 228 lotuses
Q. There is another pond in which the number of lotuses triples every day. When both the ponds had no flowers, Damayanti placed a lotus in the doubling pond. After 4 days, she took all the lotuses from there and put them in the tripling pond. How many lotuses will be in the tripling pond after 4 more days?
Answer:
In the first pond (Doubling Pond), the number of lotuses double every day, so for the first 4 days it doubles every day.
So, after the first 4 days, the number of lotuses is 1 × 2 × 2 × 2 × 2 = 24.
In the second pond (Tripling Pond), the number of lotuses triple every day, so for the next four days, they triple every day.
So, after the next 4 days, the number of lotuses is 24 × 3 × 3 × 3 × 3 = 24 × 34
Q. What if Damayanti had changed the order in which she placed the f lowers in the lakes? How many lotuses would be there?
Answer:
Suppose she placed 1 lotus in the tripling pond first, for 4 days:
Then moved it to the doubling pond for 4 days:
(3 \times 2)^4 = 6^4 = 1296 3 4 × 2 4 = (3 × 3 × 3 × 3) × (2 × 2 × 2 × 2)
(3 x 2) x (3 x 2) x (3 x 2) x (3 x 2) = (3 x 2)4 = 64
So, when we find such problems where the base numbers are different but powers are same, we just multiply the base numbers like we multiplied (3 x 2), and raise it to the power.
So, in general form:
ma × na = (mn)a , where a is a counting number
Q. Simplify 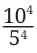 and write it in exponential form.
and write it in exponential form.
Answer:
Look at the Expression: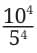 This means:
This means: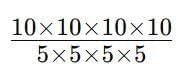
Group the Terms:
You can pair each 10 in the numerator with a 5 in the denominator:
Simplify Each Pair:
What Happened Here?
We started with 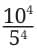 , and after simplifying, we got
, and after simplifying, we got
Notice that:
The exponent (4) stayed the same.
The base became
10 5 = 2 \frac{10}{5} = 2
So, We Can Generalize a Rule:
When you divide two powers that have the same exponent, but different bases,
you can divide the bases and keep the exponent the same.
These rules are helpful shortcuts in simplifying expressions using exponents.
Always remember:
- If bases multiply, and powers are same, combine bases.
- If bases divide, and powers are same, divide bases.
How Many Combinations
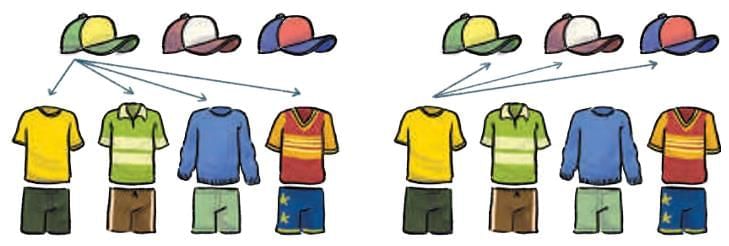
Estu has 4 dresses and 3 caps. How many different ways can Estu combine the dresses and caps?
To find the total number of combinations:
For each cap, Estu can wear 4 different dresses.
So for 3 caps:
4 + 4 + 4 = 12 combinations
Or, 4 × 3 = 12 combinations
Similarly, for each dress, he can wear 3 different caps.
So for 4 dresses:
3 + 3 + 3 + 3 = 12 combinations
Or, 3 × 4 = 12 combinations
Estu and Roxie came across a safe containing old stamps and coins that their great-grandfather had collected. It was secured with a 5-digit password. Since nobody knew the password, they had no option except to try every password until it opened. They were unlucky and the lock only opened with the last password, after they had tried all possible combinations. How many passwords did they end up checking?
To make it easier, first try a simpler version:
(a) 2-digit Lock:
Each digit has 10 options: 0 to 9
So total combinations = 10 × 10 = 100 passwords
These are: 00, 01, 02, ..., 99
(b) 3-digit Lock:
Now, add one more digit to each 2-digit password
Total = 100 (previous combinations) × 10 = 1,000 passwords
From 000 to 999
(c) 5-digit Lock:
Each digit has 10 options
So total = 10 × 10 × 10 × 10 × 10 = 100,000 passwords
From 00000 to 99999
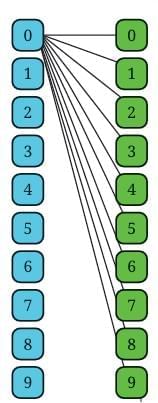
Lock Combinations
The Other Side of Powers
Imagine a line that is 16 units long.
We know:
16 = 2 × 2 × 2 × 2 = 2⁴
Now, if we erase (remove) half of the line:
We divide 16 by 2 →
16 ÷ 2 = 8
8 = 2 × 2 × 2 = 2³
Now, erase half again:
8 ÷ 2 = 4
4 = 2 × 2 = 2²
Again, erase half a third time:
4 ÷ 2 = 2
2 = 2¹
So, we started from 2⁴ and after dividing by 2 three times, we reached 2¹.
We can write this as:
2⁴ ÷ 2³ = 2¹
Or, 2⁴ ÷ 2³ = 2(4-3) = 2¹
General Rule of Dividing Powers
If you divide two powers with the same base, you subtract the exponents.
That means:
nᵃ ÷ nᵇ = n⁽ᵃ ⁻ ᵇ⁾,
where n is not zero, and a > b.
Try This
What is:
2100 ÷ 225?
Use the rule:
2¹⁰⁰ ÷ 2²⁵ = 2⁽¹⁰⁰ ⁻ ²⁵⁾ = 2⁷⁵
Why Can’t n Be 0?
We have a rule:
nᵃ ÷ nᵇ = nᵃ⁻ᵇ, where n ≠ 0
Let’s see why n cannot be 0:
Example:
Take:
2⁴ ÷ 2⁴ = 2⁴⁻⁴ = 2⁰
Now,
2⁴ = 16
So, 2⁴ ÷ 2⁴ = 16 ÷ 16 = 1
Therefore, 2⁰ = 1
In fact for any letter number a
20 = 2a – a = 2a ÷ 2a = 1.
In general,
xa ÷ xa = xa – a = x0, and so
1 = x0 ,
where x ≠ 0 and a is a counting number.
So, any number when raised to the power 0 is equals to 1.
This rule works for any number except 0.
Let’s say we halve a line of length 2⁴ = 16 units again and again:
Halve it 5 times:
2⁴ ÷ 2⁵ = 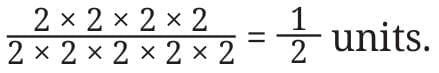
But by using the above general form we can write,
2⁴ ÷ 2⁵ = 2⁴⁻⁵ = 2⁻¹
That means: 2⁻¹ = 1 ÷ 2 =
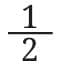
Halve it 10 times:
In general form we can write: 2⁴ ÷ 2¹⁰ = 2⁴⁻¹⁰ = 2⁻⁶
In normal form we can write: 2⁴ ÷ 2¹⁰ =
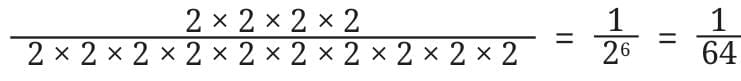
So, we learn:
n-a = 1 ÷ nᵃ, and
nᵃ = 1 ÷ n⁻ᵃ , where n is not a zero
Summary of General forms:
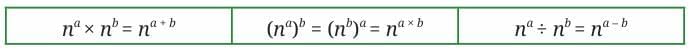
Power Lines
Power line is a line having all the powers of a number on it, this helps us in making difficult power calculations, very easy
Let us arrange the powers of 4 along a line.
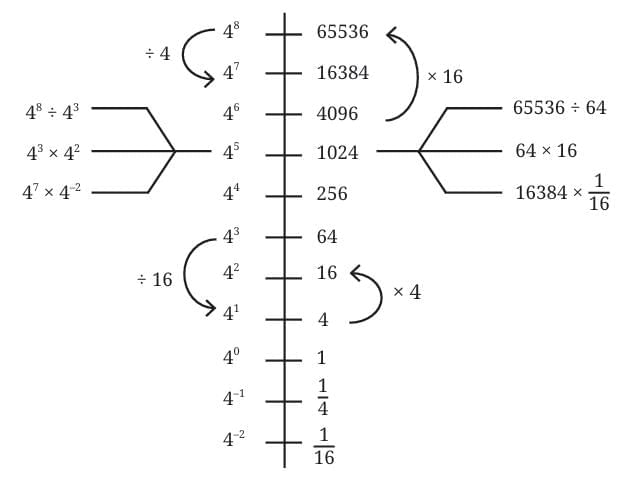
Power Line of 4
Q. Can we say that 16384 (47) is 16 (42) times larger than 1,024 (45)?
Yes, since 47 ÷ 45 = 4(7-5) = 42.
Q. How many times larger than 4–2 is 42
42 ÷ 4-2 = 4 (2-(-2)) = 4(2+2) = 44
So, 42 is 44 larger than 4–2
Powers of 10
What are Powers of 10?
"Powers of 10" means writing numbers using exponents of 10. This is a shorter and easier way to show how many times 10 is multiplied.
For example:
10 = 10¹ (10 is multiplied once)
100 = 10² (10 × 10)
1000 = 10³ (10 × 10 × 10)
Using Powers of 10 in Numbers
Let’s take a number and write it in expanded form and then in powers of 10:
Example: 47561
Expanded form:
47561 = (4 × 10000) + (7 × 1000) + (5 × 100) + (6 × 10) + (1)
Now, write these place values using powers of 10:
10000 = 10⁴
1000 = 10³
100 = 10²
10 = 10¹
1 = 10⁰
So,
Using powers of 10:
47561 = (4 × 10⁴) + (7 × 10³) + (5 × 10²) + (6 × 10¹) + (1 × 10⁰)
What about Decimal Numbers?
Let’s look at 561.903
How can we write 561.903?
Expanded form (separating whole and decimal parts):
= (5 × 100) + (6 × 10) + (1 × 1) + (9 × 1/10) + (0 × 1/100) + (3 × 1/1000)
Now, write them using powers of 10:
100 = 10²
10 = 10¹
1 = 10⁰
1/10 = 10⁻¹
1/100 = 10⁻²
1/1000 = 10⁻³
So,
Using powers of 10:
561.903 = (5 × 10²) + (6 × 10¹) + (1 × 10⁰) + (9 × 10⁻¹) + (0 × 10⁻²) + (3 × 10⁻³)
Scientific Notation
Why Do We Need Scientific Notation?
When we deal with very large numbers, it becomes hard to:
Count the number of zeroes correctly.
Place commas at the right positions.
Read or write the number without making mistakes.
Example:
It is easy to confuse ₹5,000 with ₹50,000 just because of one missing zero.
To avoid such confusion, we use a way of writing numbers called Scientific Notation (also known as Standard Form).
What is Scientific Notation?
Scientific Notation is a method to write very large or very small numbers using powers of 10.
Format:
A number in scientific notation is written as:
x × 10y,
where:
x is a number between 1 and 10 (called the coefficient),
y is an exponent (any whole number), and
10y shows how many times 10 is multiplied.
Example of Breaking a Number into Scientific Notation
Let’s take the number 5900.
We can write it in many ways using powers of 10:
5900 = 590 × 10
= 59 × 10²
= 5.9 × 10³ → This is the correct scientific notation
(Because 5.9 is between 1 and 10)
Another example:
80,00,000 = 8 × 10⁶
Why Is Scientific Notation Useful?
Let’s look at some big facts:
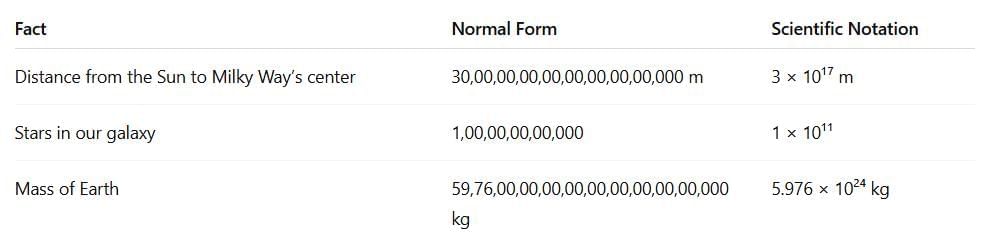
This helps us read and write large numbers easily and quickly.
Importance of the Exponent (Power of 10)
In the scientific form x × 10y, the exponent y is very important:
It tells us how big the number is.
Changing x changes the number a little.
Changing y changes the number a lot.
Example:
2 × 10⁷ = 2 crore
3 × 10⁷ = 3 crore → Only 50% more
But 2 × 10⁸ = 20 crore → 10 times more
Accuracy and Approximation
When we say Kohima has a population of 1,42,395, it seems like we are sure about the number right down to the last person.
But often, when we use big numbers, we are not always interested in the exact value. We just want to know how big the number is.
If we are only sure that the population is about 1,42,000, we can write it as:
1.42 × 10⁵If we are only sure it's about 1,40,000, we can write: 1.4 × 10⁵
In scientific notation, the number of digits in the beginning (called the coefficient) shows how accurately we know the value.

When we talk about very old things, like a dinosaur’s skeleton, we say:
"It is 70 million years old."
We don’t usually add the exact number of years (like 70 million and 15 years), because it doesn’t matter much.
These are rounded-off numbers, and that is good enough for most purposes.
We often use scientific notation to write very large distances:
Distance from Sun to Saturn:
14,33,50,00,00,000 m
= 1.4335 × 10¹² m
Distance from Saturn to Uranus:
14,39,00,00,00,000 m
= 1.439 × 10¹² m
Distance from Sun to Earth:
1,49,60,00,00,000 m
= 1.496 × 10¹¹ m
These scientific forms make large numbers easier to read and compare.
Did You Ever Wonder?
Last year, you learned some fun thinking activities (thought experiments) in your Large Numbers chapter. Let’s continue that with a new situation.
The Situation
A man named Nanjundappa wants to donate:
- Jaggery equal to the weight of Roxie
- Wheat equal to the weight of Estu
He is trying to find out how much money this donation would cost him.

How Do We Calculate the Cost?
We use these formulas:
- Cost of Jaggery = Roxie’s weight × Cost of 1 kg of jaggery
- Cost of Wheat = Estu’s weight × Cost of 1 kg of wheat
Make Assumptions (Use Reasonable Values)
If we don’t know the exact weights or prices, we can make reasonable guesses.
Let’s assume:
- Roxie is 13 years old and weighs 45 kg
- Cost of 1 kg of jaggery is ₹70
Then,
Jaggery cost = 45 × 70 = ₹3150
Now assume:
- Estu is 11 years old and weighs 50 kg
- Cost of 1 kg of wheat is ₹50
Then,
Wheat cost = 50 × 50 = ₹2500
A Cultural Tradition
This kind of donation is called Tulābhāra or Tulābhāram.
It means donating something (like jaggery, fruits, coins, etc.) equal to a person’s weight.
It is:
A symbol of devotion or surrender (bhakti)
A way of showing gratitude
A support to the community
Roxie now wonders:
If I donate 1-rupee coins equal to my weight, how many coins will I need?
To find this, you can follow these steps:
Problem Solving Steps
Step 1: Guess
Make a quick guess without doing any maths.
Step 2: Estimate & Calculate
(i) Understand the relationship:
Total weight of coins = Roxie’s weight
(ii) Make assumptions:
For example, assume 1 coin weighs 5 grams
(iii) Do the math:
Convert Roxie’s weight to grams (1 kg = 1000 grams → 45 kg = 45000 grams)
Now divide by the weight of 1 coin:
45000 ÷ 5 = 9000 coins
This is how you solve such interesting real-life math problems using logic, estimation, and some simple calculations.
Linear Growth vs. Exponential Growth

Roxie is reading a science-fiction story where someone builds a ladder to reach the Moon.
She wonders,
“If such a ladder were real, how many steps would it need?”
Make a Guess
Before calculating, try to guess:
Would the number of steps be in thousands, lakhs, crores, or even more?
Let’s Do the Math
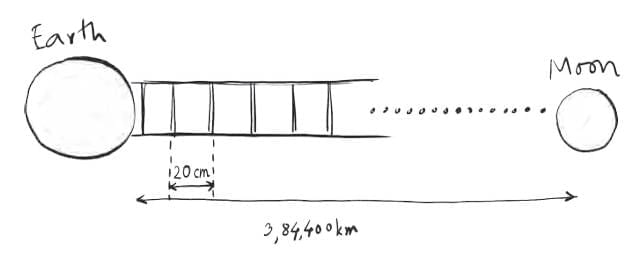
Step 1: Distance to the Moon
The Moon is about 3,84,400 kilometers away from Earth.
Step 2: Step Size
Let’s assume each step of the ladder is 20 cm apart.
(Remember: 100 cm = 1 metre, 1000 metres = 1 km)
Step 3: Convert Units
Convert 3,84,400 km to centimeters:
1 km = 1,00,000 cm
So,
3,84,400 km = 3,84,400 × 1,00,000 = 38,44,00,00,000 cm
Now divide by 20 cm (each step):
Number of steps = 38,44,00,00,000 ÷ 20 = 1,92,20,00,000 steps
(which is 192 crore and 20 lakh steps, or 1.922 billion steps)
What Is Linear Growth?
This ladder increases in a fixed way — each step is 20 cm.
So you add 20 cm every time:
20 + 20 + 20 + 20 + ... (1,92,20,00,000 times)
This kind of growth is called Linear Growth — where the value increases by the same amount each time.
What Is Exponential Growth?
Now imagine folding a piece of paper:
First fold = 2 layers
Second fold = 4 layers
Third fold = 8 layers
Fourth fold = 16 layers
and so on...
This growth multiplies each time, not adds.
This is Exponential Growth — the value doubles (or multiplies) every time.
To cover the distance between the Earth and the Moon, it takes
1,92,20,00,000 steps with linear growth whereas it takes just 46 folds of
a piece of paper.
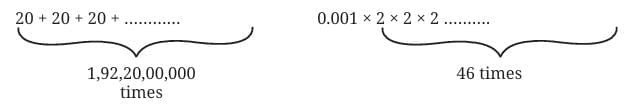
This shows how fast exponential growth can become large compared to linear growth.
Getting a Sense for Large Numbers
You have already learned:
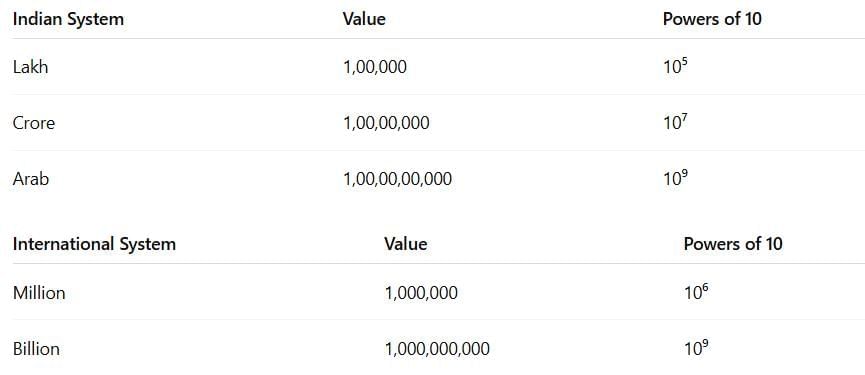
Number System
We use these systems to count very large quantities
You might know the size of the world’s human population. Have you ever wondered how many ants there might be in the world or how long ago humans emerged? In this section, we shall explore numbers significantly larger than arabs and billions. We shall use powers of 10 to represent and compare these numbers in each case.
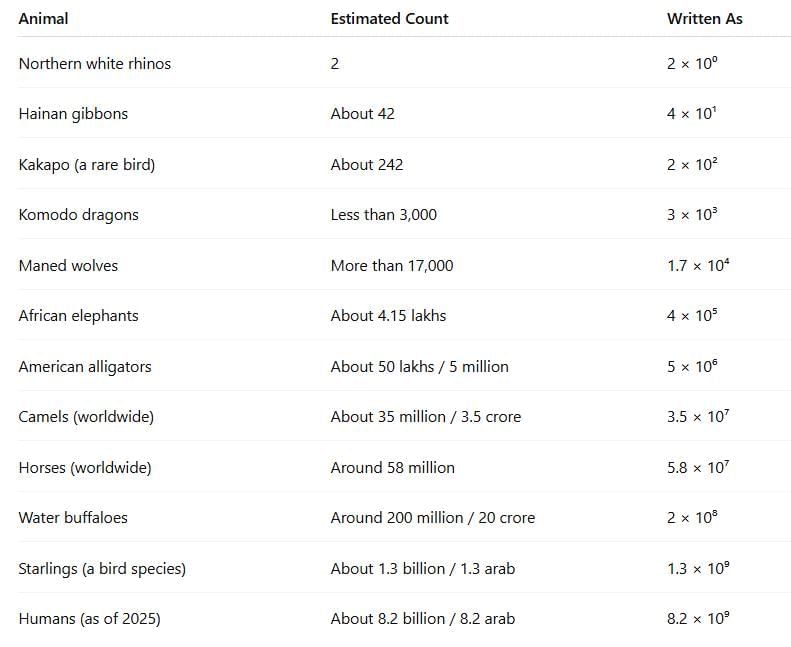
- Large numbers are easier to handle using powers of 10.
- Animal and human populations are often expressed this way to keep things simple and clear.

A picture of a starling murmuration over a farm in the UK. Starling murmuration is a mesmerising aerial display of thousands of starlings flying in synchronised, swirling patterns. It is often described as a ‘choreographed dance’.
Comparing Humans and African Elephants
Human population (2025): 8 × 10⁹
African elephant population: 4 × 10⁵
We divide:
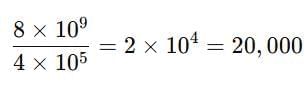
So, there are about 20,000 people for every African elephant.
We can use powers of 10 to write the population of various species:
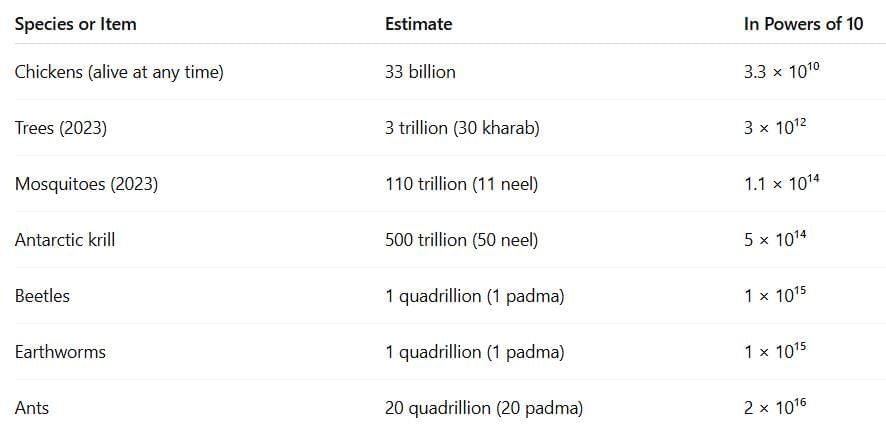
Interesting fact: Ants are so many that their total weight is more than all wild birds and mammals on Earth.
1021 is supposed to be the number of grains of sand on all beaches and deserts on Earth. This is enough sand to give every ant 10 little sand castles to live in.

A sand castle and an Ant
1023 The estimated number of stars in the observable universe is 2 × 1023.
1025 There are an estimated 2 × 1025 drops of water on Earth (assuming 16 drops per millilitre)
A different way to say your age!
“How old are you?” asked Estu.
“I completed 13 years a few weeks ago!” said Roxie.
“How old are you?” asked Estu again.
“I’m 4840 days old today!” said Roxie.
“How old are you?” asked Estu again.
“I’m ______ hours old!” said Roxie.
Make an estimate before finding this number.
Estu: “I am 4070 days old today. Can you find out my date of birth?”
If you have lived for a million seconds, how old would you be?
1,000,000 seconds ≈ 11.6 days
We shall look at approximate times and timelines of some events and phenomena, and use powers of 10 to represent and compare these quantities.
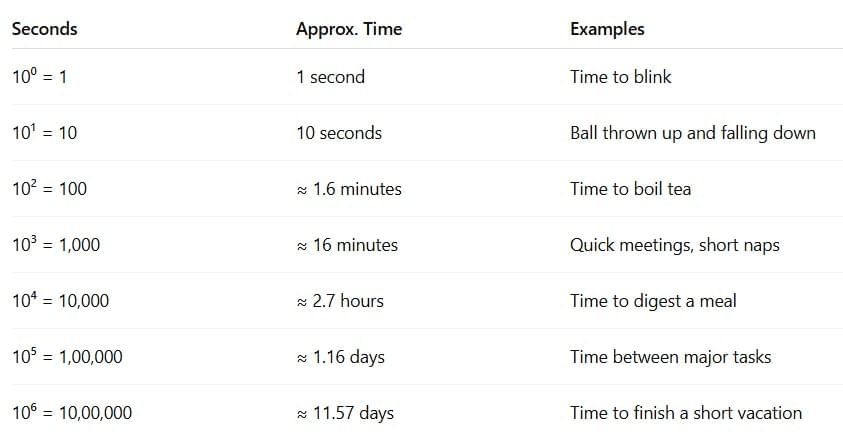
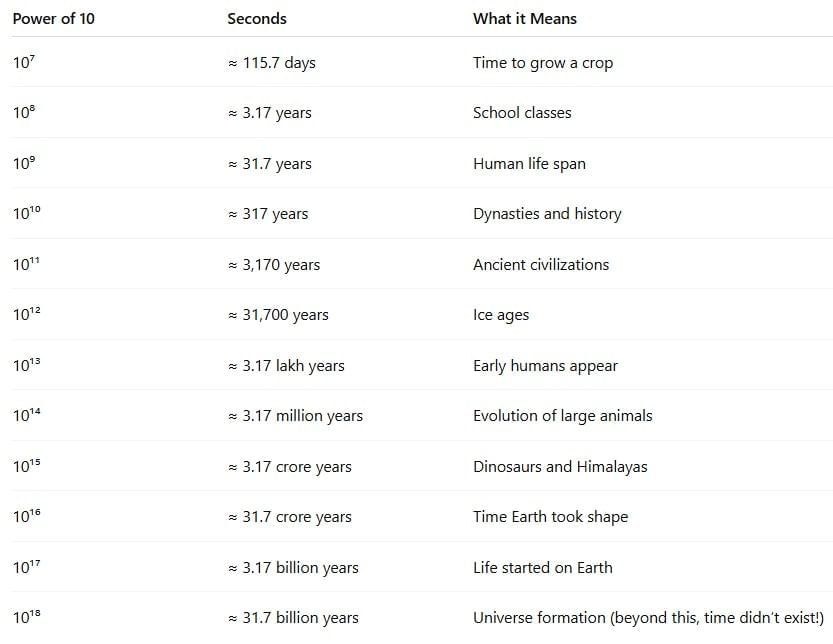
Fun Fact
10⁶ seconds is less than 2 weeks, but 10⁹ seconds is over 31 years!
This shows how fast exponential growth happens.
A Pinch of History
Ancient Indian texts like Lalitavistara, Ganita-Sara-Sangraha, and Amalasiddhi talk about extremely large numbers.
These texts belonged to Buddhist and Jaina traditions and were written over 2000 years ago.
Lalitavistara: Dialogue Between Arjuna and Prince Gautama
This is a Buddhist text from the 1st century BCE.
It gives names for very large numbers by multiplying powers of 10.
Example:
1 hundred kotis = 1 ayuta = 10⁹
1 hundred ayutas = 1 niyuta = 10¹¹
... and it continues up to 10⁵³
Other Ancient Indian Texts
- Mahaviracharya (a Jain mathematician) listed numbers up to 10²³.
A Jain text named Amalasiddhi went up to 10⁹⁶.
A grammar book by Kāccāyana (in Pali language) mentioned numbers up to 10¹⁴⁰ called asaṅkhyeya (meaning uncountable).
How They Named Large Numbers (Power Play)
They used bases like:
Sahassa = 1 thousand
Koti = 1 crore (10 million)
For example:
Prayuta (10⁶) was said as “10 hundred thousand”
This is similar to how we say:
1 lakh = 100 × 1,000 = 1,00,000 (10⁵)
1 crore = 100 × 1 lakh = 1,00,00,000 (10⁷)
1 arab = 100 × 1 crore = 10⁹
And so on…
Fun Facts About Huge Numbers
- Googol = 10¹⁰⁰ (a 1 followed by 100 zeros)
Googolplex = 10^Googol (a 1 followed by a googol of zeros)
Estimated number of atoms in the universe = between 10⁷⁸ and 10⁸²
So, googolplex is much larger than anything in the real world.
Highest Currency Notes in History
In India, the highest note is ₹2000
Hungary (1946): Printed a note of 1 sextillion pengő (10²¹) – but it was never used.
Zimbabwe (2009): Printed a note of 100 trillion dollars (10¹⁴) – it was worth only around 30 US dollars

|
13 videos|105 docs
|
FAQs on Power Play Chapter Notes - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is exponential notation and how is it used in mathematics? |  |
| 2. How do you perform operations with powers of 10? |  |
| 3. What are some common applications of powers of 10 in real life? |  |
| 4. Why is it important to understand the concept of powers and exponents? |  |
| 5. Can you explain the 'other side of powers' mentioned in the article? |  |




















