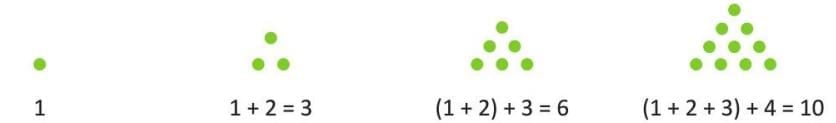Patterns Chapter Notes | Mathematics for JSS 2 PDF Download
| Table of contents |

|
| Introduction |

|
| Patterns with a Unit of Repeat |

|
| Progressive Patterns |

|
| Patterns with More Than One Characteristic |

|
| Triangular and Square Numbers |

|
Introduction
Imagine a world where everything follows a rhythm, like the beat of a drum or the colors in a rainbow! Patterns are like magical sequences that repeat or grow in a special way, making our world more interesting. In this exciting chapter, we’ll explore how shapes, numbers, and letters dance together to create patterns. From repeating designs to growing sequences and even special numbers that form triangles and squares, get ready to discover the rules that make patterns so fascinating!
Patterns with a Unit of Repeat
Patterns that have a repeating unit are called repeating patterns. These patterns can include shapes, sizes, colors, letters, or numbers. The repeating unit is the part of the pattern that keeps coming back in the same order.
- Steps to extend a repeating pattern:
- Step 1: Look at the pattern and find the unit that repeats.
- Step 2: Check for any similarities or differences, like if shapes rotate or change.
- Step 3: Study 3 or 4 consecutive items to understand the sequence, then continue the pattern.
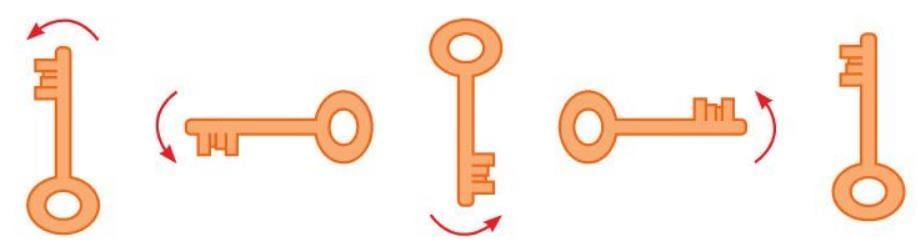
- Patterns can also involve rotation, where shapes or objects turn around their center.
- Rotations can be quarter turn (90°), half turn (180°), three-fourths turn (270°), or full turn (360°).
- Rotations happen in a specific direction: clockwise or anticlockwise.
- Example: A pattern of keys where each key turns 90° anticlockwise to form the next part of the pattern.
Pattern of Shapes

Pattern of Sizes

Pattern of Colours
Pattern of Letters

Pattern of Numbers

Progressive Patterns
- Patterns that grow in size are called progressive patterns, also known as growing or increasing patterns.
- Each element in the pattern gets bigger in a predictable way, often seen in numbers or shapes.
- Progressive patterns follow a specific rule to increase the size of elements.
- Unlike repeating patterns, progressive patterns do not have a repeating unit.
Examples
- Example (Number Pattern) 1: In the sequence 1, 3, 5, 7, …, start with 1 and add 2 to get the next number, forming a pattern of odd numbers.
- Example (Shape Pattern) 2: A pattern where each step adds one more triangle or square to the previous group, starting with one shape and increasing by one each time.

Patterns with More Than One Characteristic
- Some patterns have multiple features, like color, size, or number of holes, that define the sequence.
- These patterns may have more than one unit of repeat.
- Patterns can combine numbers and letters to create sequences.
- Such patterns are often used for coding and decoding messages.
- Example (Button Pattern) 1: A pattern of buttons where the sequence is based on color, size, and number of holes in each button.

- Example (Number and Letter Pattern) 2: The sequence A B 1 C D 2 E F 3 G H 4 combines letters and numbers in a specific order.

- Example (Coding/Decoding) 3: The code EUTIHZPI decodes to the phone number 25936073 using a given code table:
 where each letter represents a digit (e.g., E=2, U=5, T=9).
where each letter represents a digit (e.g., E=2, U=5, T=9).
Triangular and Square Numbers
- Number sequences have rules that show how each number is formed from the previous one.
- These rules help identify special sequences like triangular and square numbers.
Triangular Numbers
- Numbers that can be shown as dots arranged in a triangle shape are called triangular numbers.
- The pattern is formed by adding consecutive numbers to the previous sum.
Example: The sequence 1, 3, 6, 10, … is formed by:
- 1 = 1 dot
- 1 + 2 = 3 dots
- 1 + 2 + 3 = 6 dots
- 1 + 2 + 3 + 4 = 10 dots
Square Numbers
- Numbers that can be shown as dots arranged in a square shape are called square numbers.
- The pattern is formed by multiplying a number by itself.
Example: The sequence 1, 4, 9, 16, … is formed by:
- 1 × 1 = 1
- 2 × 2 = 4
- 3 × 3 = 9
- 4 × 4 = 16
- The sum of two consecutive triangular numbers forms a square number.
|
83 videos|193 docs|36 tests
|
FAQs on Patterns Chapter Notes - Mathematics for JSS 2
| 1. What are patterns with a unit of repeat? |  |
| 2. How can I identify progressive patterns? |  |
| 3. What do patterns with more than one characteristic mean? |  |
| 4. Can you explain triangular and square numbers? |  |
| 5. How can I create my own patterns? |  |