Number Systems Chapter Notes | Mathematics for Grade 10 PDF Download
Real Numbers
Real numbers are the numbers used in everyday life, including whole numbers, fractions, and decimals. They are organized into a hierarchical structure of sets, where smaller sets are subsets of larger ones. A number in a set is called an element, and this structure helps classify numbers systematically.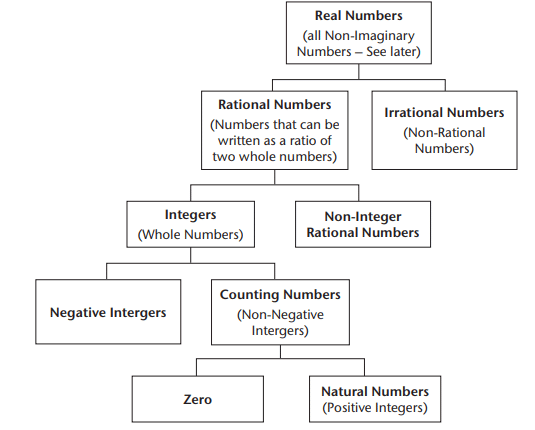
Hierarchical Structure
- Sets and Subsets: A set is a collection of numbers. Subsets are smaller sets contained within larger ones. For example, your class is a set, and you are an element. Your class is a subset of your school, which includes all students.
- Connections: The hierarchy shows how sets are linked. Numbers in a lower set (e.g., integers) are also in all sets above it (e.g., rational numbers, real numbers).
Example Relationships:
- Integers (e.g., -2, 0, 7) are a subset of rational numbers.
- Rational numbers (e.g., 0.56, 7) are a subset of real numbers.
- Irrational numbers (e.g., π ≈ 3.141592653589…) belong only to the irrational and real number sets.
- Counting numbers (0, 1, 2, …) include zero and positive integers.
- The set {0} contains only zero.
Symbols for Sets
- Real numbers: ℝ
- Rational numbers: ℚ
- Irrational numbers: ℝ - ℚ or ℚ' (real numbers excluding rationals)
- Integers: ℤ
- Non-integer rational numbers: ℚ - ℤ
- Counting numbers (non-negative integers): ℕ₀
- Positive integers (natural numbers): ℤ⁺ or ℕ
- Negative integers: ℤ⁻ or ℤ - ℕ₀
- Zero: {0}
Set Subtraction
- Definition: Excluding elements from a set (e.g., ℝ - ℚ means all real numbers except rationals, i.e., irrationals).
- Alternative Notation: Some use ℝ \ ℚ, read as "ℝ excluding ℚ."
- Terminology: ℝ - ℚ is the complement of ℚ in ℝ.
Classifying Numbers
- Example A: 2 is a natural number (ℕ), counting number (ℕ₀), rational number (ℚ), and real number (ℝ). It is not negative (ℤ⁻) or irrational (ℝ - ℚ).
- Example B: 0.5785 = 5785/10000 (a fraction), so it is a non-integer rational number (ℚ - ℤ) and real number (ℝ). It is not an integer (ℤ) or irrational (ℝ - ℚ).
- Example C: √3 is irrational (ℝ - ℚ) and real (ℝ), not rational (ℚ) or lower in the hierarchy.
- Example D: Surds like √2 are irrational unless the number is a perfect square (e.g., √1.21 = 1.1 is rational, as 1.21 = 1.1 × 1.1). For cubes, √[3]{27} = 3 is rational, but √[3]{9} is irrational.
- Example E: √-1 is imaginary, not real, and does not fit in the real number hierarchy.
Set Notation Symbols
- Subset: ⊆ (e.g., ℤ ⊆ ℚ means integers are a subset of rationals).
- Element: ∈ (e.g., 49 ∈ ℕ₀ means 49 is a counting number).
- Not an element: ∉ (e.g., 4.9 ∉ ℤ means 4.9 is not an integer).
Representing Sets and Intervals
This section explains how to represent sets of numbers using set notation, interval notation, and number lines, focusing on ordered sets where numbers can be compared.
Number Line Representation
Concept: Real numbers are points on a continuous line, with smaller numbers to the left and larger to the right, like a ruler.
Construction:
- Choose a point for 0 and another for 1 to set the scale.
- Mark other numbers by measuring distances (e.g., for 4/5, measure 0.8 of the distance from 0 to 1).
Precision: Measurements are approximate, rounded to the nearest millimetre.
Set Notation
- Definition: A set is a collection of numbers, listed in braces { } in increasing order (e.g., {1, 2, 3, 4, 5, 6} for die rolls).
- Short Form: Use … for patterns (e.g., {1, 2, 3, …, 6}).
- Elements: Numbers in the set (e.g., 2 ∈ ℤ, √2 ∉ ℤ).
- Cardinality: Number of elements (e.g., {0} has cardinality 1; ℚ between 0 and 1 is infinite).
Interval Notation
Definition: Represents numbers between two endpoints.
Symbols:
- [a, b] includes endpoints (a ≤ x ≤ b).
- (a, b) excludes endpoints (a < x < b).
- [a, b) or (a, b] for one endpoint included.
- ∞ for no upper bound, always with ) as infinity is not a number (e.g., [1/9, ∞)).
Examples:
- Real numbers between -2.4 and 4.7, including 4.7: {x ∈ ℝ | -2.4 < x ≤ 4.7} or (-2.4, 4.7].
- Integers from 5 to 99: {x ∈ ℤ | 5 ≤ x ≤ 99} or [5, 99].
- Rational numbers ≥ 1/9: {x ∈ ℚ | x ≥ 1/9} or [1/9, ∞).
Number Line Examples
- Real numbers (-2.4, 4.7]: Open circle at -2.4, closed circle at 4.7.
- Integers [5, 99]: Dots at 5, 6, …, 99.
- Rationals [1/9, ∞): Arrow from 1/9 rightward, no upper endpoint.
Rounding Off and Significant Figures
This section revises how to round off numbers to reduce unnecessary precision, commonly used in measurements.
Rounding Rules
Process: Express the number as a decimal, cut off digits after a specified place, and adjust the last digit based on the next digit.
Rule:
- If the next digit is 0–4, keep the last digit.
- If the next digit is 5–9, increase the last digit by 1.
Example: For 17.984364501:
- To 6 decimal places: 17.984365 (7th digit is 5, round 4 to 5).
- To 2 decimal places: 17.98 (3rd digit is 4, keep 8).
- To 0 decimal places: 18 (1st digit is 9, round 17 to 18).
Notes
- Always refer to the original number for each rounding, not a previously rounded version, to avoid errors.
- Rounding to 0 decimal places means rounding to the nearest whole number.
Rational Numbers in More Detail
Rational numbers can be expressed as fractions of whole numbers and are essential in measurements due to their terminating or recurring decimal forms.
Definition
- Rational Number: A number written as a/b, where a and b are integers, b ≠ 0 (e.g., 26.24 = 2624/100).
- Terminating Decimals: End after a finite number of digits (e.g., 1.2457231054472005983 is rational).
- Recurring Decimals: Digits repeat infinitely (e.g., 0.333… = 1/3, 12.146146… = 12134/999).
Converting Decimals to Fractions
- Terminating: Write as a fraction (e.g., 0.16 = 16/100 = 4/25).
- Recurring: Use algebra (e.g., for 12.146…: let x = 12.146…, 1000x = 12146.146…, subtract: 1000x - x = 12134, so x = 12134/999).
Converting Fractions to Decimals
Methods:
- Grouping: Split the fraction (e.g., 323/12 = 312/12 + 11/12 = 26 + 11/12 ≈ 26.916666…).
- Long Division: Divide numerator by denominator (e.g., 323 ÷ 12 = 26.916666…).
Result: Decimals either terminate or recur (e.g., 1/3 = 0.333…, 4/9 = 0.444…).
Measurements
- Rational by Nature: Measurements are rounded to a certain precision (e.g., 3.58 m rounded to 3.6 m for planks).
- Example: An ammeter reading 0.1 A or 0.01 A is rational, even if measuring an irrational quantity.
- Calculator Use: Can switch between decimal and fraction forms (consult calculator manual).
Irrational Numbers in More Detail
Irrational numbers cannot be written as fractions of whole numbers and have non-terminating, non-recurring decimals. They appear in specific mathematical contexts.
Key Contexts
- Circles: π (≈ 3.141592653589…) is irrational, defined as C/D (circumference/diameter).
- Surds: Roots like √2, √3 are irrational unless the number is a perfect power (e.g., √4 = 2 is rational).
- Trigonometry: Trigonometric functions often produce irrational outputs from rational inputs (see Chapter 6).
Approximating π
Geometric Method:
Draw a circle (diameter 20 cm), construct polygons (square, octagon, etc.) inside.
Calculate perimeter/diameter (C/D):
- Square: C/D ≈ 2.83.
- Octagon: C/D ≈ 3.06.
- Higher polygons approach π (e.g., 3.12).
Conclusion: π is non-terminating, non-recurring, hence irrational.
Physical Method: Roll a disc, measure circumference and diameter, calculate C/D (approximates π to 2 decimal places).
Approximating Surds
Example (√2):
- √2 is between 1 and 2 (1² = 1, 2² = 4).
- Between 1.4 and 1.5 (1.4² = 1.96, 1.5² = 2.25).
- Between 1.41 and 1.42 (1.41² = 1.9881, 1.42² = 2.0164).
Conclusion: √2 is non-terminating, non-recurring, hence irrational.
Property: √[n]{x} is irrational if x is not a perfect nth power.
Rational Approximations
- Irrational numbers (e.g., π, √2) are approximated as rationals for practical use (e.g., π ≈ 22/7, but 22/7 is less accurate than calculator’s π for circle calculations).
- Rounded values are rational but not exact (infinitely long decimals).
Binary Numbers
Binary numbers, using base 2, are fundamental to computers, which store and process data using 0s and 1s.
Decimal vs. Binary
- Decimal (Base 10): Uses digits 0–9, place values are powers of 10 (e.g., 125602.12 = 1×10⁵ + 2×10⁴ + … + 2×10⁻²).
- Binary (Base 2): Uses digits 0 and 1, place values are powers of 2 (e.g., 100100011₂ = 1×2⁸ + 1×2⁵ + 1×2¹ + 1×2⁰ = 256 + 32 + 2 + 1 = 291).
Converting Decimal to Binary
- Method 1 (Sum of Powers): Decompose into powers of 2 (e.g., 83 = 64 + 16 + 2 + 1 = 1×2⁶ + 1×2⁴ + 1×2¹ + 1×2⁰ = 1010011₂).
- Method 2 (Repeated Division):
- Divide by 2, record remainders (e.g., 83 ÷ 2 = 41 r1, 41 ÷ 2 = 20 r1, …, read remainders backward: 1010011₂)
Example: 187 = 128 + 32 + 16 + 8 + 2 + 1 = 10111011₂.
Converting Binary to Decimal
- Sum the powers of 2 for each 1 (e.g., 100111011₂ = 1×2⁸ + 1×2⁵ + 1×2⁴ + 1×2³ + 1×2¹ + 1×2⁰ = 256 + 32 + 16 + 8 + 2 + 1 = 315).
- Notation: Binary numbers use subscript 2 (e.g., 100111011₂).
Binary Arithmetic
Addition:
- Grouping: 111₂ + 101₂ = (100 + 10 + 1) + (100 + 1) = 1000 + 10 + 10 = 1100₂.
- Column: Carry over when sum ≥ 2 (e.g., 1 + 1 = 10₂, carry 1).
Subtraction:
- Grouping: 110₂ - 101₂ = (100 + 10) - (100 + 1) = 10 - 1 = 1₂.
- Column: Borrow as needed (e.g., 1011₂ - 111₂ = 100₂).
- Negative results: Compute larger - smaller, then negate (e.g., 10₂ - 11₂ = -(11₂ - 10₂) = -1₂).
Multiplication:
- Distribute: 111₂× 101₂ = 111₂ × (100 + 1) = 11100 + 111 = 100011₂.
- Column: Similar to decimal multiplication.
Division:
- Long division: 10001₂ ÷ 101₂ = 11₂ remainder 10₂.
- Grouping: 10001₂ = 101₂ × 11₂ + 10₂.
Binary Fractions
- Fractions: Use negative powers of 2 (e.g., 0.375 = 1/4 + 1/8 = 0.011₂).
- Example: 5.375 = 101.011₂ (5 = 101₂, 0.375 = 0.011₂).
- Recurring: 0.333… (decimal) = 0.010101…₂ (binary).
Other Bases
- Hexadecimal (Base 16): Uses 0–9, A–F (e.g., 2B7₁₆ = 2×16² + 11×16¹ + 7 = 695).
- Sexagesimal (Base 60): Used for angles/time (e.g., 1 minute = 1/60 degree).
Complex Numbers
Complex numbers combine real and imaginary numbers, used in advanced technical applications.
Definitions
- Imaginary Number: Involves √-1, denoted i, where i² = -1.
- Complex Number: Form a + bi, where a is real, b is imaginary (e.g., 2 + 3i, -4 + i).
- Set: Denoted ℂ.
Properties: i² = -1, so √-1 = i.
Examples:
- √-2 = √2 × i (imaginary).
- √[3]{-1} = -1 (real, as (-1)³ = -1).
- 2i × 3i = 6i² = -6 (real).
Arithmetic
- Addition: (2 + 3i) + (4 + 4i) = 6 + 7i.
- Subtraction: (-2 + i) - (3i - 5) = 3 - 2i.
- Multiplication: (2 + 3i)(-1 + 3i) = -11 + 3i.
- Division: (-4 + 6i)/2 = -2 + 3i.
Points to Remember
- Real numbers (ℝ) include rational (ℚ) and irrational (ℝ - ℚ) numbers, organized in a hierarchy (e.g., ℤ ⊆ ℚ ⊆ ℝ).
- Symbols: ℝ (real), ℚ (rational), ℤ (integers), ℕ (natural), ∈ (element), ⊆ (subset), ∉ (not an element).
- Number line: Represents real numbers as points, ordered left (smaller) to right (larger).
- Set notation: Lists numbers in braces (e.g., {1, 2, 3}); interval notation uses [a, b] or (a, b) for ranges.
- Rounding: Adjusts to specified decimal places (0–4: keep, 5–9: increase by 1).
- Rational numbers: Fractions (a/b), terminating (e.g., 0.16) or recurring (e.g., 0.333…) decimals.
- Irrational numbers: Non-terminating, non-recurring (e.g., π, √2); appear in circles, surds, trigonometry.
- Binary numbers: Base 2 (0, 1), used in computers; convert via powers of 2 or division; arithmetic mimics decimal.
- Imaginary numbers: Involve i (√-1), where i² = -1; complex numbers (a + bi) combine real and imaginary parts.
- π is irrational, approximated by polygons (e.g., octagon: C/D ≈ 3.06) or physical measurements.
- Surds are irrational unless perfect powers (e.g., √4 = 2 is rational, √3 is irrational).
- Binary fractions use negative powers of 2 (e.g., 0.5 = 0.1₂).
Difficult Words
- Hierarchy: Organized structure where smaller sets (subsets) are contained in larger sets.
- Subset: A set whose elements are all in another set (e.g., ℤ ⊆ ℚ).
- Element: A number in a set (e.g., 2 ∈ ℕ).
- Cardinality: Number of elements in a set (e.g., {0} has cardinality 1).
- Interval: Range of numbers between two endpoints (e.g., [1, 6]).
- Surd: A root (e.g., √2), irrational unless a perfect power.
- Recurring Decimal: Decimal with repeating digits (e.g., 0.333…).
- Non-terminating: Decimal that never ends (e.g., π).
- Binary: Number system using base 2 (digits 0, 1).
- Imaginary Number: Involves √-1 (i), where i² = -1.
- Complex Number: Form a + bi, combining real (a) and imaginary (bi) parts.
Summary
This chapter equips Grade 10 students with a comprehensive understanding of number systems. It classifies real numbers (ℝ) into rational (ℚ, e.g., 0.56, 1/3) and irrational (ℝ - ℚ, e.g., π, √2) sets, using symbols like ℤ (integers) and ℕ (natural numbers). Students learn to represent numbers on a number line, in set notation (e.g., {1, 2, 3}), and interval notation (e.g., [1, 6]). Rounding off simplifies measurements to rational numbers. Rational numbers are fractions with terminating or recurring decimals, while irrationals are non-terminating and non-recurring. Binary numbers (base 2) are explored for computer applications, with methods for conversion and arithmetic. Complex numbers (a + bi) introduce imaginary numbers (i = √-1), essential for advanced technical fields.FAQs on Number Systems Chapter Notes - Mathematics for Grade 10
| 1. What are real numbers and how are they classified? |  |
| 2. How do you represent sets and intervals in mathematics? |  |
| 3. What is rounding off and why is it important in mathematics? |  |
| 4. Can you explain what rational numbers are and provide examples? |  |
| 5. What are binary numbers and how do they differ from decimal numbers? |  |





















