Is This a Multiple Of?
Sum of Consecutive Numbers
Anshu is curious about writing numbers as the sum of consecutive natural numbers. He has written thefollowing—
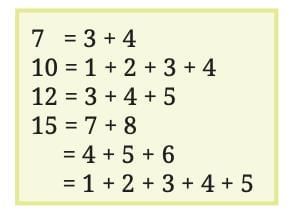 He begins experimenting and wonders about various patterns. His exploration leads to some key questions:
He begins experimenting and wonders about various patterns. His exploration leads to some key questions:
Can every natural number be written as a sum of consecutive numbers?
Which numbers can be written as sums of consecutive numbers in multiple ways?
Can all even numbers be written as a sum of consecutive numbers?
Can 0 be written as a sum of consecutive numbers, possibly using negative numbers?
Exploration:
Natural Numbers: Not all can be expressed (e.g., powers of 2 like 2, 4, 8 cannot).
Multiple Ways: Numbers like 15 have multiple representations.
Even Numbers: Some can (e.g., 12 = 3 + 4 + 5), but not all (e.g., 2).
Zero: Possible with negative numbers (e.g., -1 + 0 + 1 = 0).
Four Consecutive Numbers with + and – Signs
Take four consecutive numbers (e.g., 3, 4, 5, 6), place ‘+’ or ‘–’ between them, forming 8 expressions (2^3 due to three positions for signs). Eight such expressions are possible. You can use the diagram below to systematically list all the possibilities.
Eight such expressions are possible. You can use the diagram below to systematically list all the possibilities.
You can repeat the same pattern using any other set of four consecutive numbers as well.
Observation: It can be observed that certain sums always occur, regardless of which four consecutive numbers are chosen.
Hint: Use algebra and describe the 8 expressions in a general form.
For any four consecutive numbers n, n+1, n+2, n+3, the eight expressions are:
- n + (n+1) + (n+2) + (n+3)
- n + (n+1) + (n+2) – (n+3)
- n + (n+1) – (n+2) + (n+3)
- n – (n+1) + (n+2) + (n+3)
- n + (n+1) – (n+2) – (n+3)
- n – (n+1) + (n+2) – (n+3)
- n – (n+1) – (n+2) + (n+3)
- n – (n+1) – (n+2) – (n+3)
- All results from the evaluated expressions are even numbers, meaning they are divisible by 2.
- Negative numbers that are divisible by 2, such as –2, –4, –6, and so forth, are also considered even numbers.
- With any four consecutive numbers, regardless of how addition (‘+’) or subtraction (‘–’) signs are placed between them, the resulting expressions consistently produce even numbers.
- Examine whether each calculated expression results in an even or odd number and identify any consistent patterns.
- Experiment again with different groups of four numbers to verify if the observed pattern (e.g., all results being even) remains consistent across various sets.
Explanation1: Using Algebra - Why All 8 Expressions Have the Same Parity?
Let’s take any 4 consecutive numbers: a, b, c, and d.
Now, consider one of the 8 possible expressions, like:
a + b - c - d
Now change one sign — for example, replace +b with -b.
The new expression becomes:
a - b - c - d
Let’s find the difference between the original and the new expression:
(a + b - c - d) - (a - b - c - d)
= a + b - c - d - a + b + c + d
= 2b (which is an even number)
So, changing one sign changes the total by an even number.
Now suppose you change a negative sign to a positive sign instead.
For example, if you change -c to +c, the result again changes by an even number — specifically, 2c.
Conclusion:
Every time you change a sign in any of the 8 expressions, the value changes by an even number. This means all 8 expressions will either all be even or all be odd — they will always have the same parity.
Explanation 2: Using Rules of Odd and Even Numbers
We know some basic rules:
Odd ± Odd = Even
Even ± Even = Even
Odd ± Even = Odd
Now, let’s understand the parity (whether the result is odd or even) of expressions like:
a + b and a - b
You might have noticed that both of these will always have the same parity, no matter if a and b are odd or even.
So we can say:
a ± b always has the same parity.
Let’s build on that.
Now try:
a ± b + c and a ± b - c — even these will have the same parity.
If we keep extending this pattern, we can confidently say that:
All expressions of the form a ± b ± c ± d will have the same parity.
Conclusion:
No matter how you place the plus and minus signs among four numbers, the final result will always be either all odd or all even — but never a mix.
Explanation 3: Using the Positive and Negative Token Model
You can also understand this using the positive and negative token model you learned in the Integers chapter.
Think of each ‘+’ sign as adding a positive token and each ‘–’ sign as adding a negative token. The overall result depends on how these tokens combine.
Even though there are infinite ways to choose four numbers (a, b, c, d) and mix them with ‘+’ and ‘–’ signs, mathematical reasoning helps us avoid checking each one manually.
It proves that no matter how you place the signs, all expressions of the form a ± b ± c ± d will always have the same parity (either all odd or all even).
So, the parity stays constant, even if the numbers and signs change.
Breaking Even
Using our understanding of even numbers, we can determine which of the following arithmetic expressions result in even numbers—without actually calculating them.
We’ll use the parity rules:
Even ± Even = Even
Odd ± Odd = Even
Even × Any Number = Even
Odd ± Even = Odd
Odd × Odd = Odd
For example,
We can find which of these are even, without calculating using parity:

Expressions:
43 + 37
→ Odd + Odd = Even
672 – 348
→ Even – Even = Even
4 × 347 × 3
→ 4 is even ⇒ Even × Anything = Even
708 – 477
→ Even – Odd = Odd
809 + 214
→ Odd + Even = Odd
119 × 303
→ Odd × Odd = Odd
5133
→ Odd exponent = Odd
Let’s explore another example to see how the pattern holds.
Based on our understanding of how even and odd numbers behave during operations, let’s examine which of the following algebraic expressions always result in an even number for any integer values used.
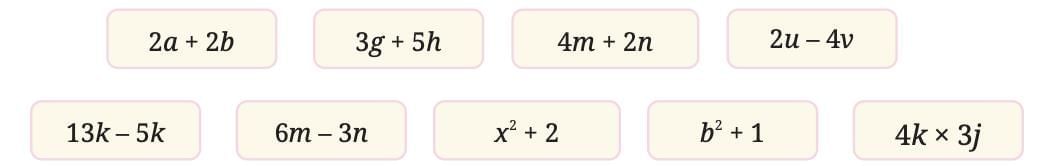
2a + 2b
Always even, because both terms are multiples of 2.
Example: a = 3, b = –4 → 2(3) + 2(–4) = 6 – 8 = –2 (even)
3g + 5h
Can be odd or even depending on values of g and h.
Example: g = 1, h = 1 → 3 + 5 = 8 (even)
g = 2, h = 1 → 6 + 5 = 11 (odd)
Not always even.
4m + 2n
Always even, both terms are even.
Example: m = 2, n = 3 → 8 + 6 = 14 (even)
2u – 4v
Always even, as both terms are even.
Example: u = 1, v = 1 → 2 – 4 = –2 (even)
13k – 5k = 8k
6m – 3n
Not always even. 6m is even, 3n is odd if n is odd.
Example: m = 2, n = 1 → 12 – 3 = 9 (odd)
Not guaranteed to be even.
b²
Square of even number → even
Square of odd number → odd
So, not always even.
Example: b = 2 → 4 (even), b = 3 → 9 (odd)
x + 1
Depends on x
x even → x + 1 = odd
x odd → x + 1 = even
So, not always even.
4k × 3j = 12kj
Always even, as 12 is even.
Example: k = 1, j = 1 → 12 (even)
Expression 1: 4m + 2q
This expression will always result in an even number for any integer values of m and q. Here's why:
Reason 1: Both 4m and 2q are always even for any integers m and q, because multiplying any number by an even number results in an even product. Their sum, therefore, is also even.
Reason 2: The expression can be rewritten as 2(2m + q), which clearly shows that 2 is a factor. So, the whole expression is divisible by 2 and thus always even.
Assuming value of m and q
If m = 4 and q = -9
4 × 4 + 2 × (-9)
= 16 - 18
= -2 (Even)
Expression 2: x² + 2
x² is even if x is even, and odd if x is odd.
So, x² + 2 will be:
Even when x is even
Odd when x is odd
This means the expression does not always result in an even number.
Assuming value of x
Your turn!
Ques: Analyse the Following Expressions.
1. 2a + 2b
 View Answer
View Answer 
Always even. Both terms are even → Sum is even
Example: a = 3, b = 5 → 6 + 10 = 16 (Even)
2. 3g + 5h
 View Answer
View Answer 
May or may not be even. Depends on values of g and h
Example: g = 1, h = 1 → 3 + 5 = 8 (Even)
Example: g = 2, h = 1 → 6 + 5 = 11 (Odd)
3. 4m + 2n
 View Answer
View Answer 
Always even. Same logic as 2a + 2b
Example: m = 1, n = 2 → 4 + 4 = 8 (Even)
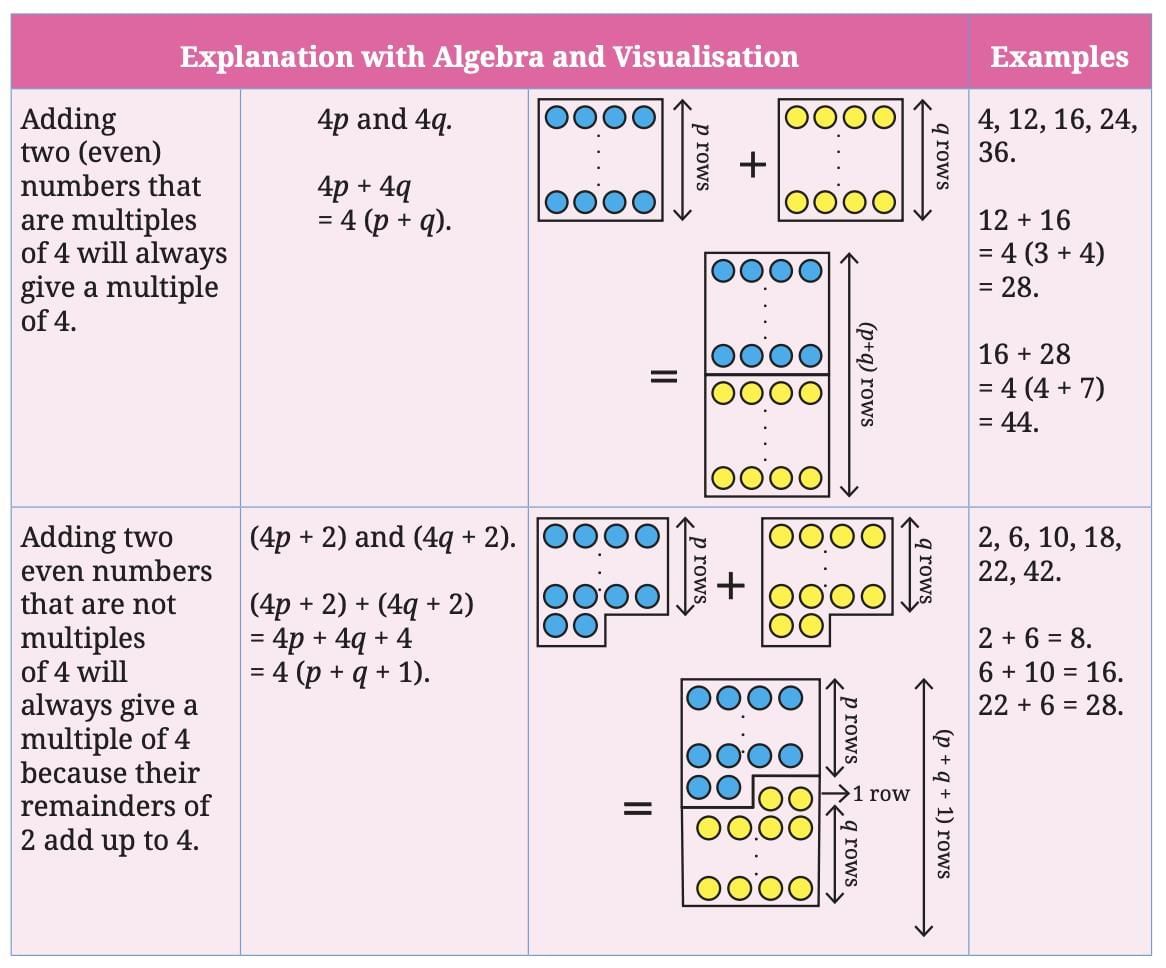
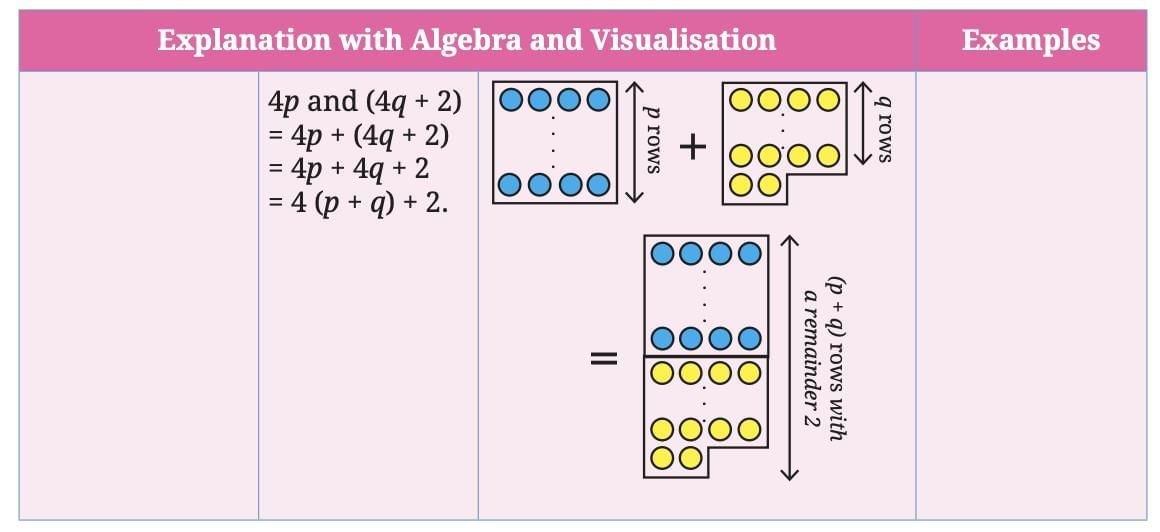
Pairs to Make Fours
Types of Even Numbers:Cases:
The table explains what happens when different types of even numbers are added together, focusing on their relationship with multiples of 4 using algebra and block visualisations for clarity.
Always, Sometimes, or Never
Statements:
1. (a) If 8 exactly divides two numbers separately, it must exactly divide their sum.
Let’s say the two numbers are:
Now, add them:
8a + 8b = 8(a + b)
Since (a + b) is a whole number, the result is clearly a multiple of 8.
So, their sum is also divisible by 8.
Example: 24 and 40
→ 8 divides 24 (8 × 3)
→ 8 divides 40 (8 × 5)
→ Sum = 24 + 40 = 64
→ 8 divides 64 (8 × 8)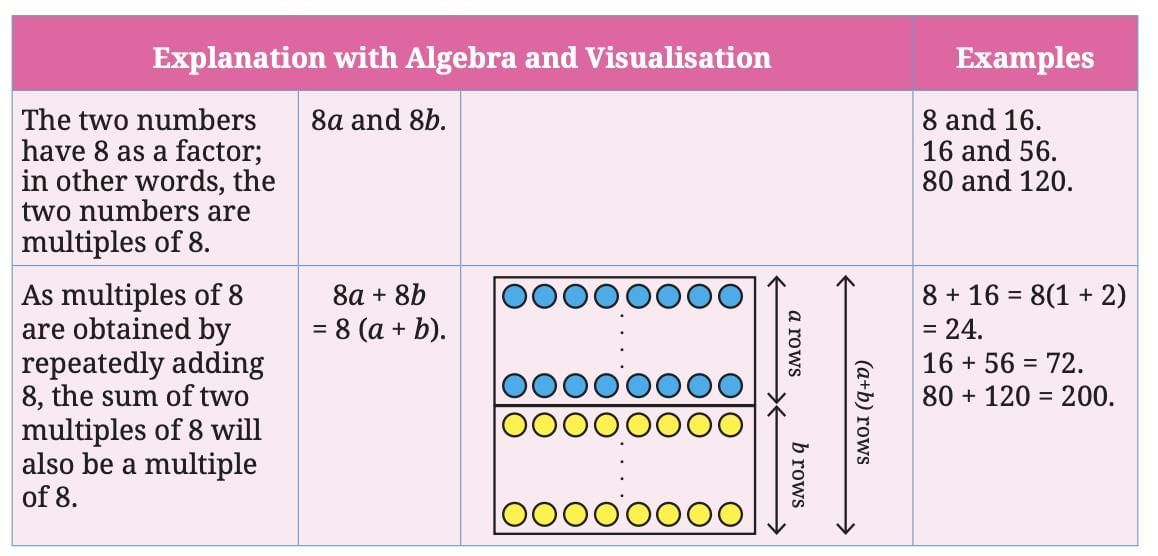
1. (b) If 8 exactly divides two numbers separately, it must also exactly divide their difference.
Let the two numbers be:
Now subtract them:
8a − 8b = 8(a − b)
Since (a − b) is a whole number, the result is still a multiple of 8.
So, their difference is also divisible by 8.
Example: 64 and 40
→ 8 divides 64 (8 × 8)
→ 8 divides 40 (8 × 5)
→ Difference = 64 − 40 = 24
→ 8 divides 24 (8 × 3)
2. If a number is divisible by 8, then 8 also divides any two numbers(separately) that add up to the number.
Case 1: When It Is Always True
If 8 exactly divides two numbers separately, it will also divide their sum.
Example:
Reason:
Multiples of 8 stay multiples when you add them together.
Case 2: When It Is Not Always True
If a number is divisible by 8, can we say that the numbers used to make it are also divisible by 8?
Example:
Reason:
The rule doesn’t work in reverse — the parts may not be divisible by 8 even if the whole is.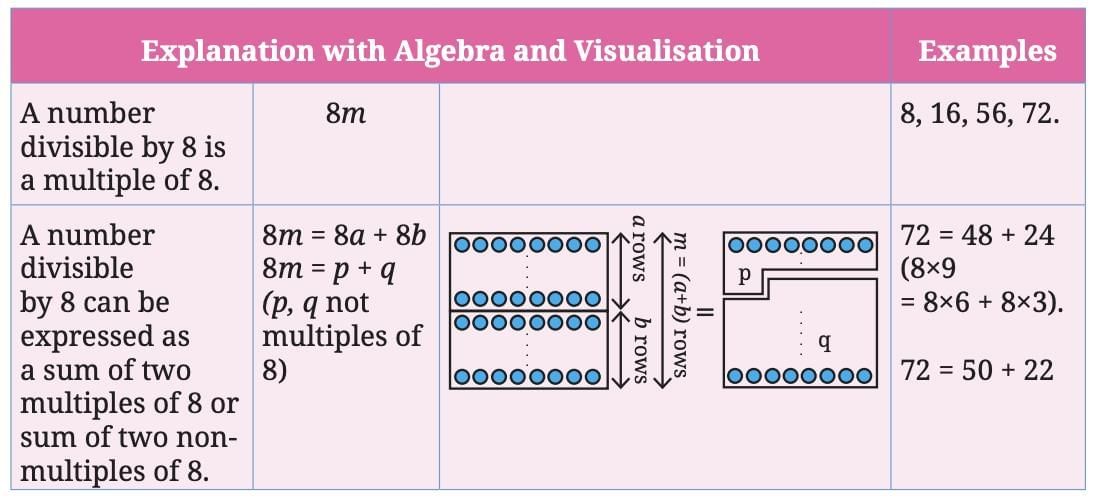
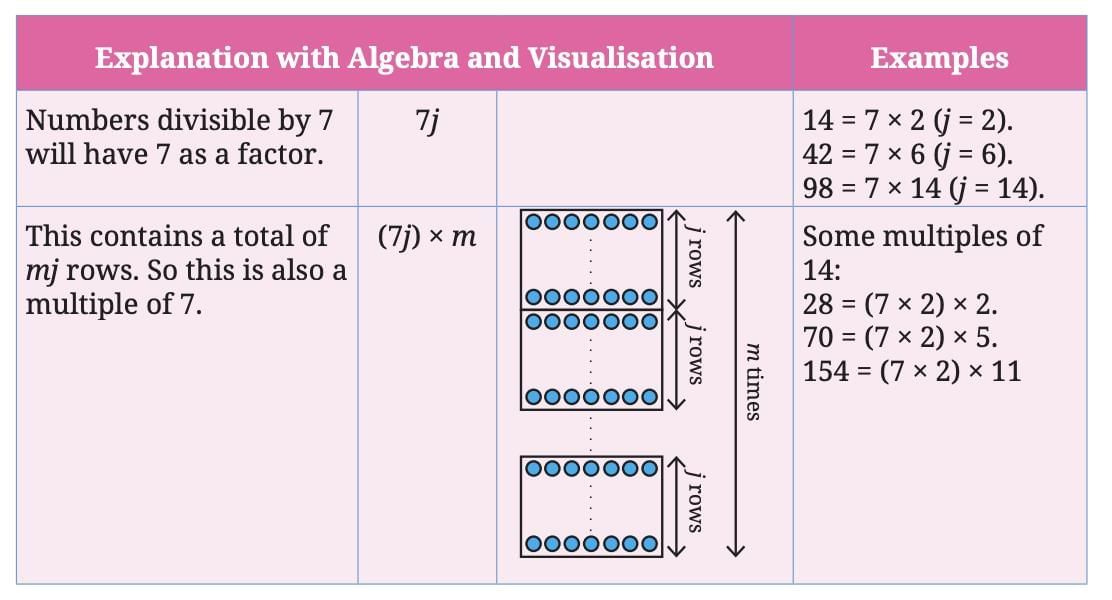
3. If a number is divisible by 7, then all multiples of that number will be divisible by 7.
Explanation:
This is always true.
If a number is divisible by 7, multiplying it by any whole number will still keep 7 as a factor.
Example:
Reason:
Multiplying a multiple of 7 keeps the factor 7 in the result.
4. If a number is divisible by 12, then the number is also divisible by all the factors of 12.
Explanation:
This is always true.
A number divisible by 12 must also be divisible by 1, 2, 3, 4, and 6 — because these are the factors of 12.
Example: 60 is divisible by 12
So, 60 ÷ 2 = 30
60 ÷ 3 = 20
60 ÷ 4 = 15
60 ÷ 6 = 10
→ Hence, 60 is divisible by all the factors of 12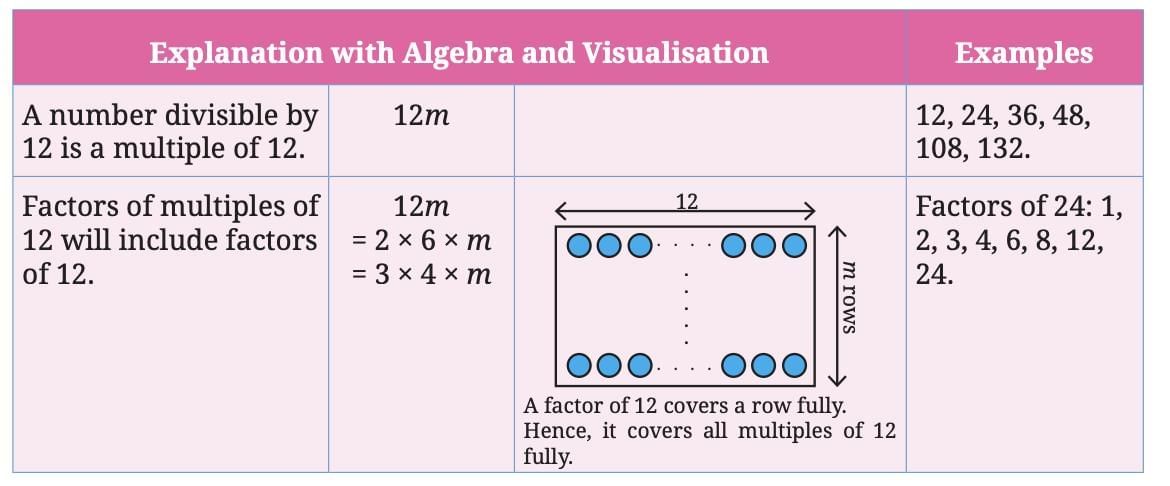
5. If a number is divisible by 7, then all multiples of that number will be divisible by 7.
Explanation:
Let’s say a number is divisible by 7. This means it can be written as 7 × k.
Now, consider another number which is a multiple of 7, say 7 × m.
The original number will be divisible by this new multiple only if m divides k.

Example where it is not true:
42 is divisible by 7 → (7 × 6)
Is 42 divisible by 28? (28 = 7 × 4)
→ 6 is not divisible by 4
→ So, 42 is not divisible by 28
Example where it is true:
6. If a number is divisible by both 9 and 4, it must be divisible by 36.
Explanation:
- Always true
- The LCM (Least Common Multiple) of 9 and 4 is 36.
- So, if a number is divisible by both 9 and 4, it is also divisible by their LCM, which is 36.
7. If a number is divisible by both 6 and 4, it must be divisible by 24.
Explanation:
- Always true
- The LCM of 6 and 4 is 24.
- A number divisible by both 6 and 4 will always be divisible by 24.
8. When you add an odd number to an even number, we get a multiple of 6.
Explanation:
- Never true
- An odd number + an even number = odd number
- But all multiples of 6 are even, so the sum cannot be a multiple of 6.
- Therefore, this is never true.
Example: 3 (odd) + 4 (even) = 7 → not a multiple of 6.
Let’s also look at this algebraically:
Now, a multiple of 6 looks like 6j (where j is any whole number)
Suppose 2(n + m) + 1 = 6j
Then:
2(n + m) = 6j – 1 → left side is even, right side is odd → not possible.
So again, this confirms the statement is never true.
What Remains?
We are looking for numbers that give a remainder of 3 when divided by 5.
Example: Try dividing the numbers below by 5:
3 ÷ 5 → remainder 3
8 ÷ 5 → remainder 3
13 ÷ 5 → remainder 3
18 ÷ 5 → remainder 3
23 ÷ 5 → remainder 3
These numbers form the list:
3, 8, 13, 18, 23, ...
All these numbers are 3 more than multiples of 5.
So, if we take multiples of 5 (like 0, 5, 10, 15, 20...), and add 3, we get our required numbers.
Thus, the general form of such numbers is:
5k + 3, where k is a whole number (k = 0, 1, 2, 3, ...)
Another form: 5k – 2
Let’s test 5k – 2 for k = 1, 2, 3...:
k = 1 → 5(1) – 2 = 3
k = 2 → 10 – 2 = 8
k = 3 → 15 – 2 = 13
k = 4 → 20 – 2 = 18
k = 5 → 25 – 2 = 23
These are the same numbers as before!
So, 5k – 2 (for k ≥ 1) also works.
Checking Divisibility Quickly
Divisibility Rules
General Form of a Number:
Let a number be written like this: … + 1000d + 100c + 10b + a,
where:
a = units digit
b = tens digit
c = hundreds digit
d = thousands digit
and so on...
Divisibility by 10
Any number can be written in expanded form using place values.
For example:
A 5-digit number edcba means:
10000e + 1000d + 100c + 10b + a
Here, every term except a (units digit) is a multiple of 10.
So, the number will be divisible by 10 only if the units digit a is 0.
Divisibility by 5
Again, in any number written as:
… + 1000d + 100c + 10b + a
Only the units digit matters for divisibility by 5.
A number is divisible by 5 only if a is 0 or 5, because all other parts are divisible by 5 already.
Divisibility by 2
All the terms except the unit digit are even (since they are multiples of 10, 100, etc.).
So, a number is divisible by 2 only if a is even (i.e., 0, 2, 4, 6, or 8).
Divisibility by 4
Let’s look at the last two digits of the number: 10b + a.
This is because all the other digits form multiples of 100, which are already divisible by 4.
So, a number is divisible by 4 if the number formed by its last two digits is divisible by 4.
Divisibility by 8
Now, we look at the last three digits: 100c + 10b + a.
This is because all the other digits are multiples of 1000, which are divisible by 8.
So, a number is divisible by 8 if the number formed by the last three digits is divisible by 8.
Divisibility by 9
A number is divisible by 9 if the sum of its digits is divisible by 9.
Example: Let’s take a number made only of 9s and 0s, like 99009.
We can break it into its place values:
99009 = 9 × 10000 + 9 × 1000 + 0 × 100 + 0 × 10 + 9 × 1
Each term is either a multiple of 9 or 0.
So any number made only of 9s and 0s is divisible by 9.
Is Looking at the Unit Digit Enough?
Can we decide if a number is divisible by 9 just by looking at its unit digit (like we do for 2 or 5)?
No. Consider:
So, the unit digit alone doesn’t help with divisibility by 9.
Why Does This Work?
Let’s take a number made only of 9s and 0s, like 99009.
We can break it into its place values:
99009 = 9 × 10000 + 9 × 1000 + 0 × 100 + 0 × 10 + 9 × 1
Each term is either a multiple of 9 or 0.
So any number made only of 9s and 0s is divisible by 9.
Important Concept: Remainders with 9
Is 10 divisible by 9?
→ No, remainder is 1 (since 10 = 9 × 1 + 1) For other multiples of 10
For other multiples of 10
- 20 ÷ 9 → remainder 2
- 30 ÷ 9 → remainder 3
- and so on...
So, any multiple of 10 leaves a remainder equal to its tens digit when divided by 9.
Similarly, for multiples of 100:
Example: Using the above observation, find the remainder when 427 is divided by 9.
Answer: Break 427 into parts: 427 = 400 + 20 + 7
Now take the remainders:
400 → remainder 4
20 → remainder 2
7 → remainder 7
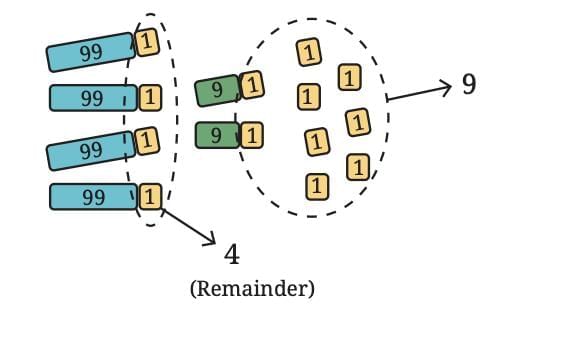 Now add:
Now add:
4 + 2 + 7 = 13
But 13 is not yet the remainder.
Do the same again:
1 + 3 = 4
So, remainder = 4
Will this work with bigger numbers?
Let’s understand a very interesting property of the number 9 and how it helps in divisibility.
We know:
This means that any power of 10 is just 1 more than a multiple of 9. So, each digit in a number shows its effect on the remainder when the number is divided by 9.
Example: 7309
Write it in its expanded form: 7309 = 7 × 1000 + 3 × 100 + 0 × 10 + 9 × 1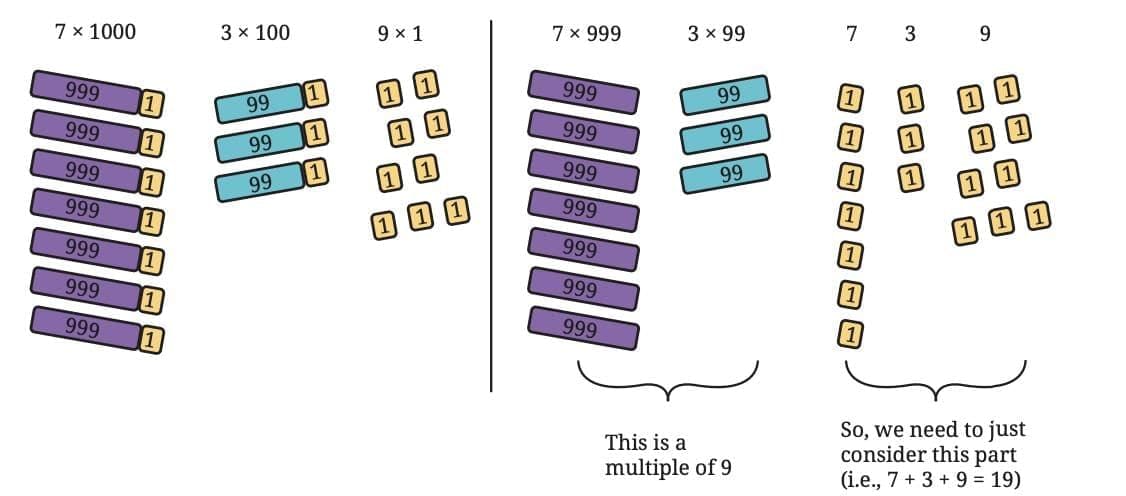
Now split the place values like we saw:
= 7 × (999 + 1) + 3 × (99 + 1) + 0 × (9 + 1) + 9 × (0 + 1)
= (7 × 999 + 3 × 99 + 0 × 9 + 9 × 0) + (7 × 1 + 3 × 1 + 0 × 1 + 9 × 1)
= (a multiple of 9) + (7 + 3 + 0 + 9)
So the number 7309 is equal to some multiple of 9 plus the sum of its digits.
Now add the digits:
7 + 3 + 0 + 9 = 19
Add again: 1 + 9 = 10
Add again: 1 + 0 = 1
So, 7309 leaves a remainder of 1 when divided by 9.
What We Learn:
A number is divisible by 9 if and only if the sum of its digits is divisible by 9.
If the digit sum is not divisible by 9, then that sum tells us the remainder.
You can keep adding the digits until you get a single digit — that final digit is the remainder when the number is divided by 9.
A Shortcut for Divisibility by 3
We already know:
All numbers divisible by 9 are also divisible by 3.
But the reverse is not true:
For example, numbers like 15, 33, and 87 are divisible by 3 but not by 9.
The Divisibility Rule for 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
A Shortcut for Divisibility by 11
This shortcut uses place values and how numbers behave when divided by 11.
Let’s break it down place by place:
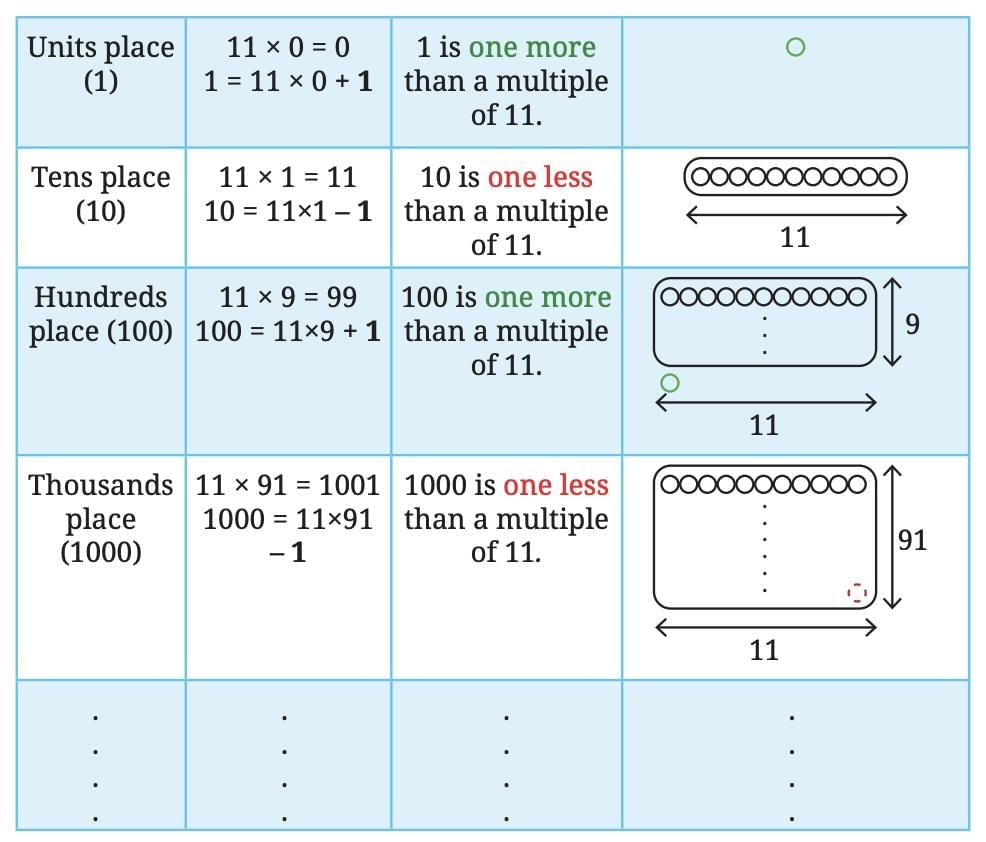
Example: Let’s look at how place values behave in a number like 462 and how they relate to the number 11.
Understanding the Pattern:
When we break down the number 462:
400 = 4 hundreds → It is 4 more than 396, which is a multiple of 11.
60 = 6 tens → It is 6 less than 66, another multiple of 11.
2 = 2 units → It is 2 more than 0, which is also a multiple of 11.
So we see that:
Hundreds place: adds a number more than a multiple of 11 (+4)
Tens place: subtracts a number less than a multiple of 11 (–6)
Units place: adds a number more than a multiple of 11 (+2)
This pattern alternates:
Add, Subtract, Add, Subtract, and so on.
Do this:

Note: General Method (Short) for Divisibility by 11
Label digits from right: 1st, 2nd, 3rd, etc.
Add digits at odd positions = S₁
Add digits at even positions = S₂
Subtract: D = S₁ – S₂
Check:
Example
Divisibility by 6 and 24
Divisibility by 6
A number is divisible by 6 if it is divisible by both 2 and 3.
Examples:
Divisibility by 24
- Checking for divisibility by 4 and 6 is not sufficient.
- Check divisibility by 3 and 8 instead.
- Reason: 24 = 3 × 8 (where 3 and 8 are co-prime).
- Example: 12 is divisible by 4 and 6 but not by 24.
Digital Roots
The digital root of a number is found by adding its digits repeatedly until a single-digit number remains.
Example: 489710
→ 4+8+9+7+1+0 = 29
→ 2+9 = 11
→ 1+1 = 2
Properties of Digital Roots:
The digital root of a multiple of 9 is always 9.
The digital root of a number shows a pattern related to its divisibility.
Used for checking divisibility, especially for 9.
Exploration Tasks:
Numbers between 600 and 700 with:
- Digital root 5 → e.g. 608 (6+0+8 = 14 → 1+4 = 5)
- Digital root 7 → e.g. 607
- Digital root 3 → e.g. 621
Digital roots of 12 consecutive numbers → Repeat in a pattern from 1 to 9 and then loop.
Digital roots of multiples of:
- 3 → 3, 6, 9, 3, 6, 9... (cycle)
- 4 → 4, 8, 3, 7, 2, 6, 1, 5, 9...
- 6 → 6, 3, 9, 6, 3, 9...
Numbers 1 more than multiples of 6 → Digital roots: 7, 4, 1, 7, 4... (pattern)
Historical Note:
Aryabhata II (c. 950 CE) used the digital root method in Mahāsiddhānta for checking arithmetic calculations.
Digits in Disguise
Cryptarithms
Rules
Each letter = one digit
No digit is used for more than one letter
First digit of a number ≠ 0
Solve by logical deduction and place value
Example: PQ × 8 = RS
Condition: A 2-digit number × 8 must give another 2-digit number.
Try values from 10 upward:
10 × 8 = 80 → same units digit (0), so invalid.
11 × 8 = 88 → repeated digits, invalid.
12 × 8 = 96 → valid: both numbers have distinct digits.
From 13 × 8 = 104, product becomes 3-digit, so only values ≤12 are allowed.
Only 12 × 8 = 96 fits all rules.



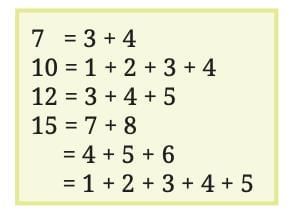 He begins experimenting and wonders about various patterns. His exploration leads to some key questions:
He begins experimenting and wonders about various patterns. His exploration leads to some key questions:



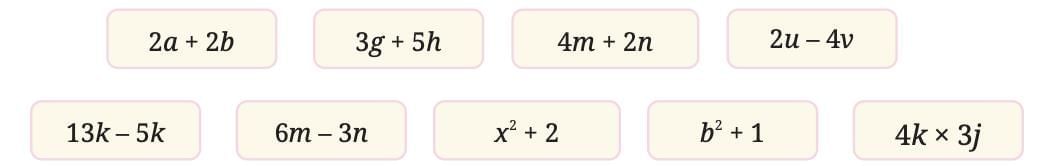














 Now add:
Now add:

















