Grade 9 Exam > Grade 9 Notes > AP Statistics > Chapter Notes: Confidence Intervals for the Difference of Two Means
Confidence Intervals for the Difference of Two Means Chapter Notes | AP Statistics - Grade 9 PDF Download
Sometimes in statistical studies, it is important to compare two different populations to see if they are different. For instance, what if we want to compare the weights of two types of apples:  ? Perhaps we believe that the weight of
? Perhaps we believe that the weight of  is more than
is more than  or maybe we just think they are different. Either way, we have the statistical means to check if the weights are different or if one weighs more than the other. One option of comparing these two populations is to create a confidence interval for the difference of two population means.
or maybe we just think they are different. Either way, we have the statistical means to check if the weights are different or if one weighs more than the other. One option of comparing these two populations is to create a confidence interval for the difference of two population means.
Conditions
As with any act of statistical inference, we must check our conditions for inference prior to performing any calculations.
Random
It is absolutely essential that your samples come from a randomized process since we seek to infer things about a population. Since we are dealing with two populations, both samples must be random. If you are performing an experiment to check the difference in two populations, you must verify that both samples were randomly assigned to treatments.
Independent
Since we are generally sampling without replacement, we must check to be sure that the samples are independent. We can use this by checking the 10% condition for both samples. NOTE: If doing an experiment, it is not necessary to check the 10% condition. A randomized experiment is sufficient for independence.
Normal
To check normality of a sampling distribution for the difference in two population means, we have to ensure that both samples have approximately normal sampling distributions. This can be done using the Central Limit Theorem (n ≥ 30), verifying that both populations are normally distributed, or by checking that box plots of both samples show no strong skewness or apparent outliers.
Calculations
To calculate a confidence interval for the difference in two population means, we must first calculate our point estimate and margin of error.
Point Estimate
Our point estimate is what we believe the difference between the two populations is, based on our sample means. To find this, we simply subtract our two sample means.
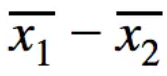
Margin of Error
Our margin of error is what we add/subtract to our point estimate to create our confidence interval. For a confidence interval for the difference of two population means, the formula for margin of error is below:
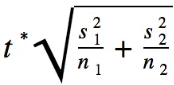
Calculator Commands
A much easier, more efficient way of calculating a confidence interval for the difference in two population means is to use technology such as a graphing calculator. On a TI-84, you would start by going into the stats menu, scrolling to test and selecting 2 Sample T Interval, where you would input the given statistics to calculate the confidence interval.
Example
Let's say that we have a bag of green apples and a bag of red apples and we want to estimate the difference in population means of the two types of apples. Our sample of 30
 s weighs a mean of 5 oz with a standard deviation of 0.2 oz, and our sample of 30
s weighs a mean of 5 oz with a standard deviation of 0.2 oz, and our sample of 30  s weighs a mean of 4.5 oz with a standard deviation of 0.15 oz. Create and interpret a confidence interval for the difference in the two population means of the weights of green apples and red apples.
s weighs a mean of 4.5 oz with a standard deviation of 0.15 oz. Create and interpret a confidence interval for the difference in the two population means of the weights of green apples and red apples.The easiest way to construct your interval is to use technology such as a graphing calculator:
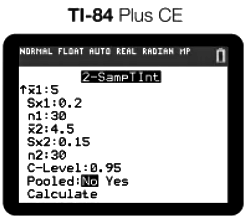 We always select not pooled when doing two sample intervals and tests because we do not know if the populations have equal variances. After calculating, we get the following interval: (0.408, 0.592).
We always select not pooled when doing two sample intervals and tests because we do not know if the populations have equal variances. After calculating, we get the following interval: (0.408, 0.592).Question for Chapter Notes: Confidence Intervals for the Difference of Two MeansTry yourself: What must be true for samples when comparing two populations?View Solution
Key Terms to Review
- 2 Sample T Interval: A statistical method used to estimate the confidence interval for the difference between the means of two independent groups.
- Central Limit Theorem: States that the sampling distribution of the sample mean approaches a normal distribution as the sample size increases.
- Confidence Interval: A range of values derived from sample statistics that is likely to contain the true value of an unknown population parameter.
- Independent Events: Two or more events that do not influence each other's occurrence.
- Margin of Error: Quantifies the uncertainty associated with a sample estimate.
- Not Pooled: Refers to a statistical approach where the variances of two populations are considered unequal.
- Point Estimate: A single value that serves as an approximation of a population parameter.
- Standard Deviation: A measure of the amount of variation or dispersion in a set of values.
The document Confidence Intervals for the Difference of Two Means Chapter Notes | AP Statistics - Grade 9 is a part of the Grade 9 Course AP Statistics.
All you need of Grade 9 at this link: Grade 9
|
12 videos|106 docs|12 tests
|
FAQs on Confidence Intervals for the Difference of Two Means Chapter Notes - AP Statistics - Grade 9
| 1. What are the conditions that must be met before calculating a confidence interval for the difference of two means? |  |
Ans. The conditions that must be met include: (1) Random: Both samples must come from a randomized process. (2) Independent: The samples should be independent, which can be checked using the 10% condition if sampling without replacement. (3) Normal: The sampling distributions should be approximately normal, which can be ensured by having sample sizes of at least 30, verifying that populations are normally distributed, or checking for skewness and outliers in box plots.
| 2. How do you calculate the point estimate for the difference of two means? |  |
Ans. The point estimate is calculated by subtracting the mean of the second sample from the mean of the first sample. It represents the estimated difference between the two population means based on the sample data.
| 3. What is the formula for margin of error when calculating a confidence interval for the difference of two means? |  |
Ans. The margin of error for the difference of two population means is calculated based on the standard error of the difference and the critical value from the t-distribution corresponding to the desired level of confidence.
| 4. Why should you select "not pooled" when calculating the confidence interval for two sample means? |  |
Ans. You should select "not pooled" because we typically do not know if the populations have equal variances. Using the not pooled approach allows for a more accurate estimation of the confidence interval by accounting for the possibility that the variances are unequal.
| 5. How can technology assist in calculating a confidence interval for the difference of two means? |  |
Ans. Technology, such as a graphing calculator like the TI-84, can simplify the calculation process. By navigating to the stats menu and selecting the 2 Sample T Interval option, you can input the necessary statistics, and the calculator will compute the confidence interval efficiently.
Related Searches















