Grade 9 Exam > Grade 9 Notes > AP Statistics > Chapter Notes: Carrying Out a Test for the Difference of Two Population Means
Carrying Out a Test for the Difference of Two Population Means Chapter Notes | AP Statistics - Grade 9 PDF Download
Overview of the Two-Sample T-Test
Once you've confirmed that the assumptions for a two-sample t-test are satisfied, you can proceed to evaluate whether the difference between two population means is statistically significant. This involves computing the test statistic and determining the p-value, which helps assess whether the observed difference between sample means is likely due to chance.
Steps for Conducting the Test
Calculating the Test Statistic
To compute the test statistic for a two-sample t-test, follow these steps:
- Find the difference between the two sample means (mean1 - mean2).
- Calculate the standard error of the difference, which accounts for the standard deviations and sample sizes of both groups.
- Divide the difference by the standard error to obtain the t-score.
The formula for the t-score, specific to comparing two population means, is simplified as:
t = (mean1 - mean2) / sqrt((s1²/n1) + (s2²/n2))
This formula is available on the AP Statistics Formula Sheet, adjusted for the two-sample case.
Question for Chapter Notes: Carrying Out a Test for the Difference of Two Population MeansTry yourself: What is the first step in calculating the test statistic for a two-sample t-test?View Solution
Determining Degrees of Freedom
Degrees of freedom (df) are essential for interpreting the t-score:
- Manual Calculation: Take the smaller of the two sample sizes and subtract 1 (similar to single-sample t-tests in Unit 7.5).
- Using Technology: When using a graphing calculator or statistical software, the degrees of freedom are provided in the output.
Critical Value (t-score)
To calculate our critical value, we used the typical formula:
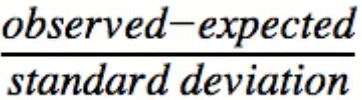To make it more specific for a t-score with the difference of two population means, our formula simplifies to: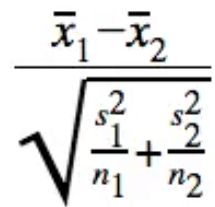
Finding the P-Value
The p-value indicates the probability that the observed difference between sample means occurred by random chance. To find it:
- Manual Approach: Use a t-table with the calculated degrees of freedom. Locate the row for your df and find the t-score closest to your calculated value. The corresponding tail probability is an approximate p-value.
- Technology Approach: Perform a two-sample t-test using a graphing calculator or software. Input either the summary statistics (means, standard deviations, sample sizes) or raw data in lists. The output will include the t-score, degrees of freedom, and p-value.
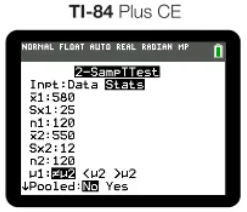And our output would be as follows: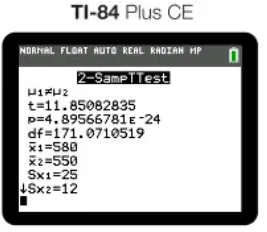
AP Exam Tip: Always report the t-score, degrees of freedom, and p-value in your response to earn full credit.
Testing the Statistical Claim
Compare the p-value to the significance level (typically α = 0.05):
- If the p-value is less than the significance level, reject the null hypothesis. This suggests strong evidence supporting the alternative hypothesis.
- If the p-value is greater than or equal to the significance level, fail to reject the null hypothesis, indicating insufficient evidence to support a difference.
Example: Green Bean Fields
Consider a scenario from Unit 7.8 where we compare the mean number of green beans picked from two fields (Field A and Field B). After performing a two-sample t-test, suppose the output is:
- t-score: [calculated value]
- Degrees of freedom: [calculated df]
- P-value: ~0.000
Conclusion: Since the p-value (~0.000) is less than 0.05, we reject the null hypothesis. There is convincing evidence that the true mean number of green beans picked from Field A differs from that of Field B. This conclusion is contextualized to the problem, compares the p-value to the significance level, and clearly states the decision regarding the null and alternative hypotheses.
Question for Chapter Notes: Carrying Out a Test for the Difference of Two Population MeansTry yourself: What do degrees of freedom help interpret?View Solution
Key Terms to Understand
- Alternate Hypothesis: A statement proposing a difference, effect, or relationship in a statistical test, contrasting the null hypothesis. It guides the test by suggesting there is an effect worth investigating.
- Degrees of Freedom: The number of independent values that can vary in a statistical calculation without violating constraints. It affects the distribution of the test statistic and is critical for hypothesis tests and confidence intervals.
- Null Hypothesis: A baseline assumption that there is no effect or difference in the population, used as a starting point for statistical testing.
- Significance Level (α): The threshold (e.g., 0.05) for deciding whether to reject the null hypothesis, representing the probability of a Type I error (false positive).
- Standard Error: A measure of how accurately a sample mean represents the population mean, quantifying variability. It is used in hypothesis tests and confidence intervals to assess precision.
- Statistical Significance: The likelihood that an observed result is not due to chance, determined by comparing the p-value to the significance level. A significant result supports rejecting the null hypothesis.
- Type I Error: Incorrectly rejecting a true null hypothesis, also known as a false positive, indicating a nonexistent effect or difference.
- Type II Error: Failing to reject a false null hypothesis, missing a true effect or difference in the population.
- Two-Sample T-Test: A statistical test to compare the means of two independent groups, assuming normal distribution and similar variances in the populations.
The document Carrying Out a Test for the Difference of Two Population Means Chapter Notes | AP Statistics - Grade 9 is a part of the Grade 9 Course AP Statistics.
All you need of Grade 9 at this link: Grade 9
|
12 videos|106 docs|12 tests
|
FAQs on Carrying Out a Test for the Difference of Two Population Means Chapter Notes - AP Statistics - Grade 9
| 1. What is a Two-Sample T-Test ? |  |
Ans.A Two-Sample T-Test is a statistical method used to determine if there is a significant difference between the means of two independent groups. It helps in comparing the average outcomes from two different populations or conditions.
| 2. When should I use a Two-Sample T-Test ? | |
Ans.A Two-Sample T-Test should be used when you want to compare the means of two independent samples to see if they are significantly different from each other. This is applicable in experiments, surveys, or observational studies where you have two separate groups.
| 3. What are the assumptions of the Two-Sample T-Test ? | |
Ans.The assumptions of the Two-Sample T-Test include: 1) the samples are independent of each other, 2) the data in each group are normally distributed, and 3) the variances of the two groups are equal (for the standard version of the test). If these assumptions are violated, alternative methods may need to be considered.
| 4. How do I interpret the results of a Two-Sample T-Test ? | |
Ans.To interpret the results of a Two-Sample T-Test, you look at the p-value obtained from the test. If the p-value is less than the significance level (commonly set at 0.05), you reject the null hypothesis, concluding that there is a significant difference between the two group means.
| 5. What is the difference between a Two-Sample T-Test and a Paired T-Test ? | |
Ans.The main difference is that a Two-Sample T-Test compares two independent groups, while a Paired T-Test compares two related groups or measurements taken from the same group at different times. The choice of test depends on the nature of your data and the relationship between the samples.
About this Document
Sep 02, 2025
Last updated
Related Exams
Document Description: Chapter Notes: Carrying Out a Test for the Difference of Two Population Means for Grade 9 2025 is part of AP Statistics preparation.
The notes and questions for Chapter Notes: Carrying Out a Test for the Difference of Two Population Means have been prepared according to the Grade 9 exam syllabus. Information about Chapter Notes: Carrying Out a Test for the Difference of Two Population Means covers topics
like Overview of the Two-Sample T-Test, Steps for Conducting the Test and Chapter Notes: Carrying Out a Test for the Difference of Two Population Means Example, for Grade 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Carrying Out a Test for the Difference of Two Population Means.
Introduction of Chapter Notes: Carrying Out a Test for the Difference of Two Population Means in English is available as part of our AP Statistics
for Grade 9 & Chapter Notes: Carrying Out a Test for the Difference of Two Population Means in Hindi for AP Statistics course.
Download more important topics related with notes, lectures and mock test series for Grade 9
Exam by signing up for free. Grade 9: Carrying Out a Test for the Difference of Two Population Means Chapter Notes | AP Statistics - Grade 9
Description
Full syllabus notes, lecture & questions for Carrying Out a Test for the Difference of Two Population Means Chapter Notes | AP Statistics - Grade 9 - Grade 9 | Plus excerises question with solution to help you revise complete syllabus for AP Statistics | Best notes, free PDF download
Information about Chapter Notes: Carrying Out a Test for the Difference of Two Population Means
In this doc you can find the meaning of Chapter Notes: Carrying Out a Test for the Difference of Two Population Means defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Carrying Out a Test for the Difference of Two Population Means theory, EduRev gives you an ample number of questions to practice Chapter Notes: Carrying Out a Test for the Difference of Two Population Means tests, examples and also practice Grade 9
tests
Related Searches
shortcuts and tricks
,ppt
,Free
,Carrying Out a Test for the Difference of Two Population Means Chapter Notes | AP Statistics - Grade 9
,study material
,video lectures
,Important questions
,Semester Notes
,Previous Year Questions with Solutions
,past year papers
,practice quizzes
,mock tests for examination
,Exam
,Objective type Questions
,Viva Questions
,Sample Paper
,Carrying Out a Test for the Difference of Two Population Means Chapter Notes | AP Statistics - Grade 9
,Carrying Out a Test for the Difference of Two Population Means Chapter Notes | AP Statistics - Grade 9
,Summary
,Extra Questions
,MCQs
;
Additional Information about Chapter Notes: Carrying Out a Test for the Difference of Two Population Means for Grade 9 Preparation
Chapter Notes: Carrying Out a Test for the Difference of Two Population Means Free PDF Download
The Chapter Notes: Carrying Out a Test for the Difference of Two Population Means is an invaluable resource that delves deep into the core of the Grade 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Carrying Out a Test for the Difference of Two Population Means now and kickstart your journey towards success in the Grade 9 exam.
Importance of Chapter Notes: Carrying Out a Test for the Difference of Two Population Means
The importance of Chapter Notes: Carrying Out a Test for the Difference of Two Population Means cannot be overstated, especially for Grade 9 aspirants.
This document holds the key to success in the Grade 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Carrying Out a Test for the Difference of Two Population Means
Chapter Notes: Carrying Out a Test for the Difference of Two Population Means Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Carrying Out a Test for the Difference of Two Population Means.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Carrying Out a Test for the Difference of Two Population Means Notes on EduRev are your ultimate resource for success.
Chapter Notes: Carrying Out a Test for the Difference of Two Population Means Grade 9 Questions
The "Chapter Notes: Carrying Out a Test for the Difference of Two Population Means Grade 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Grade 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Carrying Out a Test for the Difference of Two Population Means on the App
Students of Grade 9 can study Chapter Notes: Carrying Out a Test for the Difference of Two Population Means alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Carrying Out a Test for the Difference of Two Population Means,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Carrying Out a Test for the Difference of Two Population Means is prepared as per the latest Grade 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup