A Story of Numbers Chapter Notes | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
| Table of contents |

|
| Reema’s Curiosity |

|
| Some Early Number Systems |

|
| The Idea of a Base |

|
| Place Value Representation |

|
Reema’s Curiosity
- One lazy afternoon, Reema was reading an old book.
- Suddenly, a piece of paper fell out. It had strange symbols on it.
- Curious, she ran to her father and asked what the symbols meant.
- Her father explained that the symbols were numbers used about 4000 years ago in a region called Mesopotamia.
- Mesopotamia is an ancient civilisation located in what is now Iraq and nearby countries.
Reema’s eyes lit up, “Seriously? These strange symbols were numbers?” Her curiosity was sparked, and questions started swirling in her head.

The Human Need to Count
Even in the Stone Age, humans needed to count:
- Food supplies
- Number of animals
- Trade of goods
- Offerings in rituals
- Tracking days (for example, to predict full moon or seasons)
But they did not use the same number symbols we use today.
Origin of Modern Number System
Our number system, both spoken and written, started thousands of years ago in India.
Ancient Indian texts like the Yajurveda Samhita had names for numbers such as:
- One → Eka
- Ten → Dasha
- Hundred → Shata
- Thousand → Sahasra
- Ten thousand → Ayuta
- … and continued up to very large numbers like 10¹².
The Digits 0–9
- The way we write numbers using 0–9 started around 2000 years ago in India.
- The earliest written example of this system was found in the Bakhshali manuscript (around the 3rd century CE).
- In this manuscript, the digit 0 was written as a dot.
- The mathematician Aryabhata (around 499 CE) explained how to do proper calculations using these digits.
Spread of Indian Numerals to the World
- Around 800 CE, the Indian number system spread to the Arab world.
- Two famous Arab scholars helped:
- Al-Khwārizmī wrote a book called On the Calculation with Hindu Numerals.
- Al-Kindi wrote On the Use of the Hindu Numerals.
These works helped make Indian numerals popular in the Arab world.
Spread to Europe
- Around 1100 CE, the Indian number system reached Europe and Africa.
- An Italian mathematician named Fibonacci (around 1200) strongly supported the use of Indian numerals in Europe.
- But Europeans were used to Roman numerals, so the new system was not adopted quickly.
- By the 17th century, scientists realized that Indian numerals made calculations easier and more efficient, so they became widely used.
Why Are They Sometimes Called Arabic Numerals?
- European scholars learned these numbers from the Arabs, so they mistakenly called them Arabic numerals.
- However, Arab scholars themselves called them Hindu numerals, giving credit to India.
Today, many books and scholars use the correct terms:
- Hindu numerals
- Indian numerals
- Or the combined term Hindu-Arabic numerals
Note: The word Hindu here refers to the people of India, not the religion.
Evolution of Digits
- The digits 0 to 9 did not always look like they do today.
- Their shapes changed gradually over time until they became the symbols we now use.
Different Number Systems Before
- Before the Indian number system became popular worldwide, many civilisations had their own ways of writing numbers.
- In this chapter, you will learn about some of those systems.
- These systems are not shown in historical order but in a way that helps you understand how the idea of writing numbers developed.
French mathematician Pierre-Simon Laplace said:
“The method of expressing every number with just 10 symbols, using place value, was developed in India.
It looks simple now, but it made calculations much easier and helped mathematics grow.”
- Reema’s small discovery led to a big journey through history and mathematics.
- The way we write and use numbers today is the result of thousands of years of development — and it all started in ancient India.
The Mechanism of Counting
Imagine You Live in the Stone Age
Let's go back in time, around 10,000 years ago, when people lived in the Stone Age.
Suppose you own a herd of cows.
You don’t have numbers like 1, 2, 3, 4, or words like “three” or “five” to count or compare things.
The Natural Questions You Might Ask
If you had cows, here are some common questions:
Q1: How can we check if all the cows have come back after grazing?
Q2: Do we have fewer cows than our neighbour?
Q3: If we have fewer cows, then how many more cows do we need to have the same number as our neighbour?
The Problem
Back then, people did not have:
Number names (like one, two, three)
Written symbols (like 1, 2, 3)
So, how could they count or compare without numbers?
A Simple Solution — Using Objects Like Sticks
People used things around them, such as:
Pebbles
Sticks
Seeds
Let’s focus on using sticks.
Method 1: Counting with Sticks
For each cow, you keep one stick.
If you have 10 cows, you keep 10 sticks.
After grazing, if you collect sticks as each cow returns, you can check if any cow is missing by seeing if all sticks are used.

What Is This Method Called?
This method is called "one-to-one mapping":
One cow is matched with one stick.
No cow shares a stick with another cow.
This helps in counting and keeping track.
Representing Numbers with Sticks
Over time, this method helped people create a way to represent numbers. For example:
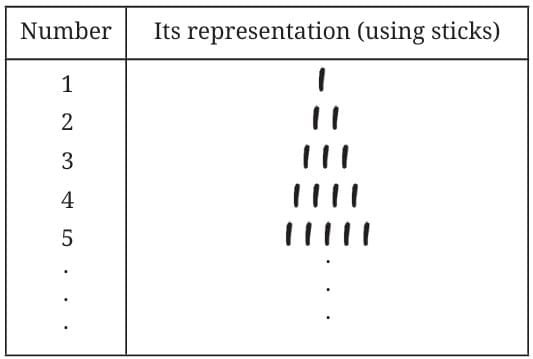
You already know how to count your own cows by making one stick per cow. Now let’s compare with your neighbour.
Q2: Do we have fewer cows than our neighbour?
Step 1: Your neighbour does the same thing: they lay out one stick for each of their cows.
Step 2: Place your stick‐pile next to your neighbour’s stick‐pile.
Step 3: See which pile is shorter.
If your pile is shorter, you have fewer cows.
If your pile is longer, you have more cows.
If they are equal, you both have the same number of cows.
Q3: How many more cows do we need to match our neighbour?
Step 1: Line up sticks from both piles side by side, one at a time.
Step 2: Continue pairing until one pile runs out of sticks.
Step 3: Count the remaining sticks in the neighbour’s pile.
Those leftover sticks tell you exactly how many cows you still need.
Method 2: Using a Sequence of Sounds (or Names)
Instead of objects, you can use a fixed sequence of sounds or names to count. Here’s how:
Choose a sequence—for example, the letters of a language (a, b, c, …).
One-to-one mapping:
First object → first sound (or name)
Second object → second sound
Third object → third sound
… and so on.
This way, each object (cow) gets a unique sound, and the last sound you speak tells you how many objects there are.
Example: Using English Letters
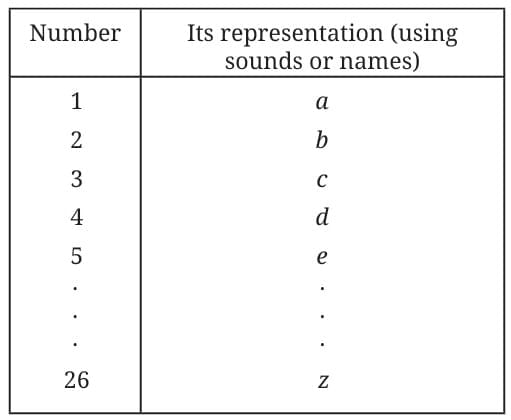
- If you have 5 cows, you go “a, b, c, d, e.”
- The last letter you say is e, which stands for 5.
Limitation
- Using only the 26 letters a … z lets you count only up to 26 objects.
- To count more, you would need additional sounds or names (for example, “aa,” “ab,” etc.), and a rule to extend the sequence.
How Many Numbers Can Be Represented Using Sounds of Letters?
From Method 2, we saw that we can use letters (like a, b, c...) to count.
But that system only lets us count up to the number of letters in the alphabet.
For example, using the English alphabet, we can count only up to 26 (z).
To count more than 26, we would need to invent more sounds or combine letters (like aa, ab…), which can get confusing.
So, we now look at Method 3.
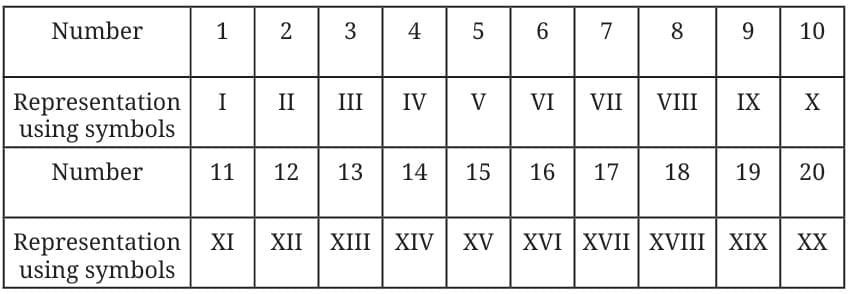
Method 3: Using a Sequence of Written Symbols (Roman Numerals)
In this method, we use a set of special symbols to represent numbers.
This was actually used in Europe long ago, before the modern number system came into use.
It is called the Roman Number System.
Examples of Roman Numerals
Here’s a part of the system:
Can This Method Be Extended for Bigger Numbers?
Yes, Roman numerals can go beyond 20, but as numbers grow larger:
- The symbols become longer and more complex.
- You need to learn more and more symbols to represent bigger numbers.
So, while this system worked for many years in Europe, it was not ideal for doing fast calculations or writing very large numbers.
What Is a Number System?
From all the methods we’ve seen (sticks, sounds, symbols), we learn:
To count anything, we need a standard sequence.
This sequence could be:
Physical objects (like sticks, pebbles)
Spoken names (like a, b, c…)
Written symbols (like I, II, III or 1, 2, 3)
We call this standard sequence a number system.
One-to-One Mapping
To count a group of things:
You map (match) each object with one part of the number system (one stick, one name, or one symbol).
This is called one-to-one mapping.
Challenges with Each Method
| Method | Type | Advantage | Disadvantage |
|---|---|---|---|
| Method 1 | Sticks (Physical Objects) | Simple and unending | Not practical for large numbers (you need too many sticks) |
| Method 2 | Sounds (Letters/Names) | Easy to say and remember | Limited — you run out of letters |
| Method 3 | Symbols (Roman Numerals) | Useful and common in Europe | Can’t easily represent very large numbers; symbols get too long |
What Are Numerals?
The symbols used in any written number system are called numerals.
Examples in the Hindu number system (what we use today) are:
0, 1, 2, 5, 36, 193, etc.Each numeral usually has a name too (like "five", "thirty-six").
Different societies used different number systems:
Some used only objects or names.
Others, like the Chinese, used all three forms: objects, names, and symbols.
Some Early Number Systems
I. Use of Body Parts

II. Tally Marks on Bones and Other Surfaces
What are Tally Marks?
- A tally mark is a simple line or notch made to count things.
- People used to cut marks on surfaces like bones, rocks, or cave walls.
- These marks were made one by one as each item was counted.
- For example, if someone had to count 5 animals, they would make 5 separate marks like this:
| | | | |
How Tally Marks Were Used
- Each mark represented one object.
- The total number of marks showed the total number of things counted.
- This method is similar to counting with sticks, but instead of collecting sticks, they just made a line or cut to show the count.
Discovery of Ancient Tally Marks
- Scientists called archaeologists have found old bones with tally marks on them.
- These bones are believed to be used for counting thousands of years ago.
Important Discoveries

Ishango Bone:
Found in the Democratic Republic of Congo.
It is between 20,000 to 35,000 years old.
It has notches in columns that may have been used as a kind of calendar.
Lebombo Bone:
Found in South Africa.
It is even older – around 44,000 years old.
It has 29 notches, and may have been used to track the moon, like a lunar calendar.
It is one of the oldest tools used for counting.
III. Number Names Obtained by Counting in Twos
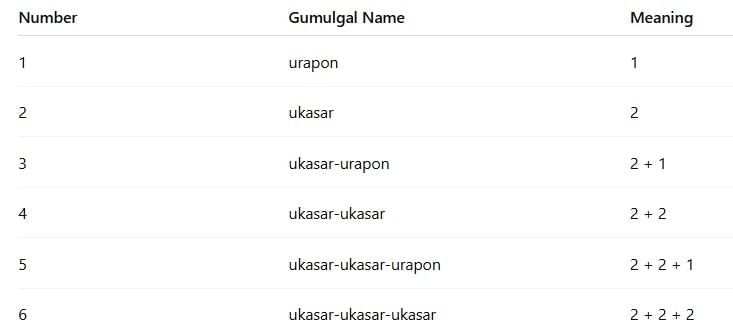
Some people in the world used very different ways to count and name numbers. One group like that is the Gumulgal, an indigenous (native) community in Australia.
2. How did the Gumulgal count numbers?
They used a system based on counting in 2s. Let’s look at how they named numbers:

For any number more than 6, they simply used the word "ras".
So basically:
They built new number names by adding more 2s and sometimes a 1.
It’s like saying:
3 = 2 + 1
4 = 2 + 2
5 = 2 + 2 + 1
6 = 2 + 2 + 2
Is this counting style only used by Gumulgal?
Surprisingly, no. Other faraway groups of people used similar systems, even though they never met each other.
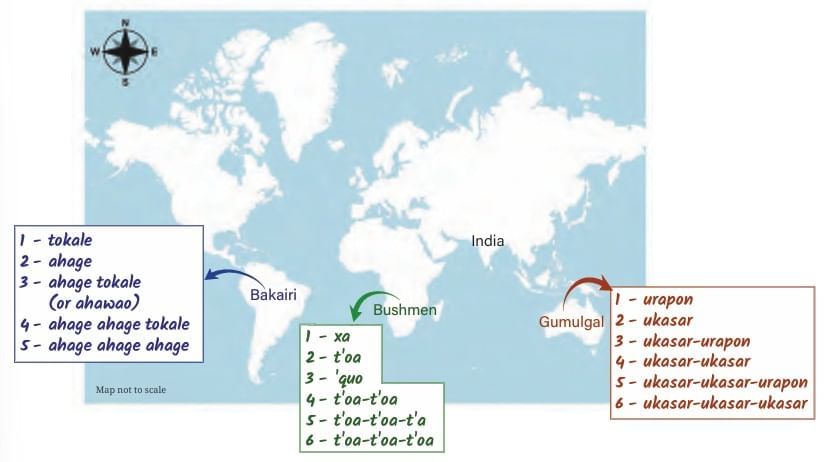
Example 1: Bakairi people (South America)
1 = tokale
2 = ahage
3 = ahage tokale (2 + 1)
4 = ahage ahage tokale (2 + 2 + 1)
5 = ahage ahage ahage (2 + 2 + 2)
Example 2: Bushmen (South Africa)
1 = xa
2 = t'oa
3 = 'quo
4 = t'oa-t'oa (2 + 2)
5 = t'oa-t'oa-t’a (2 + 2 + 1)
6 = t'oa-t'oa-t'oa (2 + 2 + 2)
Even though they lived in different parts of the world, their number names look very similar.
Historians were puzzled. These groups never met or contacted each other. Still, their number systems are very alike. One idea is that all of them may have come from common ancestors, and later spread to different places.
Why is counting in 2s important?
It's better than tally marks, where we just keep adding one line for each number.
In the Gumulgal system, using 2s helped them make numbers faster.
This idea of group counting became important in many number systems around the world.
Common group sizes used in history:
2 (like Gumulgal)
5 (used in Roman numerals like V = 5)
10 (our current system, based on fingers)
20 (used by some tribes)
Why did humans think of group counting?
Quickly count the number of objects in each of the following boxes:

You can tell the number easily only up to 4 or 5 objects.
For example:
You can recognize 2 Chicken at a glance.
But you will need to count if there are 7.
This limit of human eyesight and memory made people start grouping numbers for easier counting.
Problem with group counting
Let’s say you use only 5s to count. Then how will you write a number like 1345?
You will need to do:
5 + 5 + 5… many times, which is slow and confusing.
So, even though grouping is better than tally marks, it becomes difficult for big numbers.
People refined (improved) this idea further, which led to the advanced number systems we use today—like the decimal system based on 10.
IV. The Roman Numerals

What are Roman numerals?
Roman numerals are a number system used in ancient Rome. Instead of digits like 1, 2, 3... they used letters from the alphabet as symbols for numbers.
Basic Roman symbols
These are the main symbols used in the Roman numeral system:
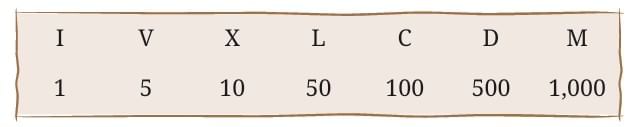
These special numbers with their own symbols are called landmark numbers.
How to write Roman numerals?
To write a number in Roman numerals:
- Break the number into groups of 10s, 5s, and 1s.
- Use the correct symbols to show each part.
Example: Write 27 in Roman numerals
Let’s break it down:
27 = 10 + 10 + 5 + 1 + 1
So we write:
10 = X
10 = X
5 = V
1 = I
1 = I
Answer: 27 = XXVII
Symbols for bigger numbers
If we keep repeating symbols like:
50 = XXXXX
That becomes long and difficult. So, a new symbol was made:L = 50
So now:40 = 50 – 10 = XL
This is like how 4 is written as:
5 – 1 = IV
But people were not always consistent. Sometimes, 40 was just written as:
XXXX (10 + 10 + 10 + 10)
How to write big numbers?
We keep subtracting from the number using landmark values.
Example: Write 2367 in Roman numerals
Break it down:
2367 = 1000 + 1000 + 100 + 100 + 100 + 50 + 10 + 5 + 1 + 1
Now use Roman symbols:
1000 = M (2 times → MM)
100 = C (3 times → CCC)
50 = L
10 = X
5 = V
1 = I (2 times → II)
Answer: 2367 = MMCCCLXII
Compared to some earlier number systems, the Roman number system was much more efficient.
It developed from the ancient Greek number system around the 8th century BCE in Rome.
Over time, it spread across Europe as the Roman Empire grew.
Why Was It Efficient?
The Roman system used groups of numbers to represent values.
These groups are based on what we now call landmark numbers (like I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000).
For example:
Instead of writing 10 separate ‘I’s to show the number 10, they used just one ‘X’.
Using such landmarks saved time and space and made numbers easier to write.
But Was It Good for Calculations?
Not really.
Even though Roman numerals were efficient for writing numbers, they were not very useful for calculations.
Doing addition, subtraction, multiplication or division using Roman numerals is hard.
Try adding these Roman numerals:
CCXXXII + CCCCXIIIFirst, count how many I’s, X’s, and C’s there are.
Group them using the largest possible landmark.
For example: 5 C’s = D (500)
Even a simple addition like this becomes complicated without converting to our modern number system.
Try It Yourself
Add: LXXXVII + LXXVIII
Then, think:
How would you multiply Roman numbers like:V × L
L × D
V × D
VII × IX
Now try multiplying:
CCXXXI × MDCCCLII
It’s not easy!

How Did People Calculate Then?
- People in Roman times used a special tool called the abacus.
- Only specially trained people knew how to use it for calculations.
- We'll learn more about the abacus later.
- Don't think that every new number system was just an improvement of the older one.
- The development of number systems is complex and not always clearly understood.
- This is true for both the Roman system and the systems we will study next.
The Idea of a Base
I. The Egyptian Number System
The Egyptian Number System was developed by the ancient Egyptians around 3000 BCE (more than 5000 years ago). It is a way of writing numbers using special symbols. Egyptians did not use digits like 1, 2, 3... like we do. Instead, they grouped numbers using landmark numbers.
What are Landmark Numbers?
Landmark numbers are important base numbers used to build other numbers.
In the Egyptian system, these landmark numbers are:
1
10 (which is 10 × 1)
100 (which is 10 × 10)
1,000 (which is 10 × 100)
10,000 (which is 10 × 1,000)
... and so on.
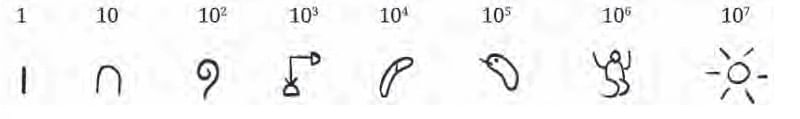
So, each new landmark number is 10 times the previous one. These are all powers of 10
How Are Numbers Built Using Landmark Numbers?
To build any number, Egyptians:
Start with the biggest landmark number that is less than or equal to the given number.
Then they count how many times that landmark number fits into the number.
Then they go to the next smaller landmark number and repeat.
They keep doing this until the full number is formed.
Symbols for Landmark Numbers
Each landmark number had its own symbol. So instead of writing 100 as "100", they would draw a specific symbol that means 100.
Example: Writing 324
Let’s break down the number 324 using landmark numbers.
The largest landmark number less than 324 is 100.
How many 100s are in 324?
→ 3 times 100 = 300What is left?
→ 324 – 300 = 24Next largest landmark number less than 24 is 10.
How many 10s are in 24?
→ 2 times 10 = 20What is left?
→ 24 – 20 = 4The last part is 4, which is made up of 1s.
So,
324 = 100 + 100 + 100 + 10 + 10 + 1 + 1 + 1 + 1
The Egyptians would use:
3 symbols of 100
2 symbols of 10
4 symbols of 1
to write the number 324.

II. Variations on the Egyptian System and the Notion of Base
In the Egyptian system, we group numbers by multiplying by 10 each time.
But what if we change this idea?
What if instead of grouping 10 collections to get the next landmark number, we use 5 collections?
Can we still build a number system that way?
Yes—we can. And we can also do the same using any positive number, like 2, 3, 4, or even 7.
Building a New Number System with 5 as the Base
Let’s try making a number system using 5 instead of 10.
We begin like this:
First landmark number = 1
Group 5 of these → 5 (second landmark number)
Group 5 of these → 25 (third landmark number)
Group 5 of these → 125 (fourth landmark number)
So each time, we multiply the previous landmark number by 5.
This gives us a new system with these landmark numbers:
1 (which is 5⁰)
5 (5¹)
25 (5²)
125 (5³)
625 (5⁴)
3125 (5⁵)
... and so on.
These are called the powers of 5.
Writing a Number in This New System (Base-5 System)
Let’s write the number 143 using this base-5 system.
We do this by:
Starting with the largest landmark number smaller than 143.
Then subtract and continue with the next lower landmark number, and so on.
Let’s break 143:
The largest landmark number less than 143 is 125 (which is 5³)
143 – 125 = 18
The next landmark number is 25, but 25 is bigger than 18, so skip it
Next is 5
18 – 5 = 13
13 – 5 = 8
8 – 5 = 3Then we move to 1s
3 – 1 = 2
2 – 1 = 1
1 – 1 = 0
So we have used:
1 of 125
3 of 5
3 of 1
143 = 125 + 5 + 5 + 5 + 1 + 1 + 1
This is how we write 143 in the base-5 system.
What Is a Base-n System?
We call a number system a base-n system if:
It starts with 1 as the first landmark number, and
Every next landmark number is made by multiplying the previous one by a fixed number n.
Examples:
Base-10 system (like the Egyptian system): 1, 10, 100, 1000... (powers of 10)
Base-5 system (like the one we just made): 1, 5, 25, 125... (powers of 5)
Our regular number system (what we use daily) is also a base-10 system.
That’s why it is called the decimal system.
The landmark numbers of a base-n number system are the powers of n starting from n0 = 1, n, n2, n3,...
Advantages of a Base-n System
What is the advantage of having landmark numbers that are all the powers of a number?
To understand this, let us perform some arithmetic operations using them.
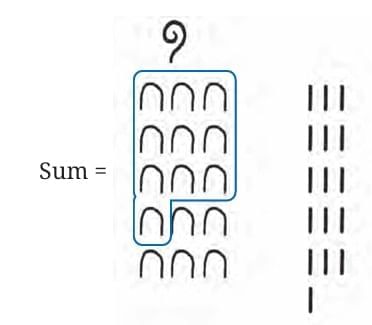
Example: Add the following Egyptian numerals:
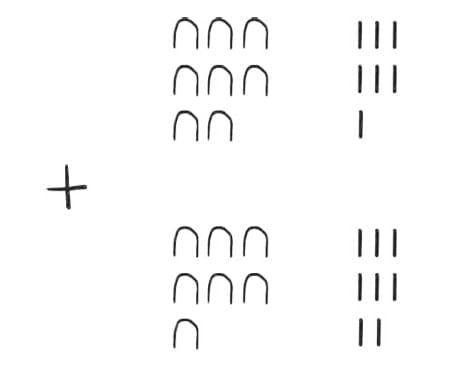
Let us find the total number of | and 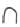 and group them starting from the largest possible landmark number. It has a total of
and group them starting from the largest possible landmark number. It has a total of
15 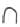 and 15 |.
and 15 |.
Since 10 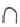 gives the next landmark number
gives the next landmark number 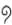 the sum can be regrouped as:
the sum can be regrouped as:
Since 10| gives a 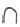 , we have:
, we have:
See how similar they are
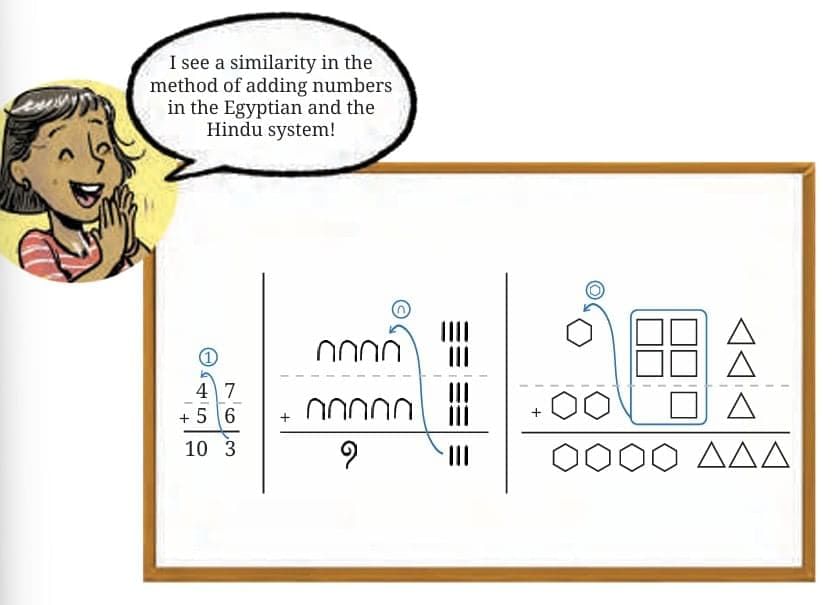
- In a base-n number system, addition is done differently compared to the Roman numeral system.
- In the Roman system, you must be careful when grouping and rearranging numbers, as they don’t always group by the same size to reach the next value.
- This careful grouping can make addition more complex in the Roman system because it relies on specific landmark numbers like I, V, X, L, C, D, and M.
- For example, to move from IV (4) to V (5), you simply add one more unit, but moving from IX (9) to X (10) requires a different approach, as it involves removing the smaller value and adding a larger one.
- On the other hand, a base-n system simplifies addition because it follows a consistent pattern based on the base.
- In these systems, you can easily add numbers without worrying about rearranging them in complicated ways to reach the next value.
- The benefits of a base number system become even clearer when you look at multiplication.
- In base-n, multiplication can be done quickly and systematically, making it easier to handle larger numbers compared to the Roman system.
What would be a simple rule to multiply a number with 
- The process of multiplying two numbers involves using landmark numbers.
- When these landmark numbers are powers of a number, their product is also a landmark number.
- This characteristic makes multiplication easier.
- However, this is not true for Roman numerals, which makes multiplication using them more challenging.
- A number system that has landmark numbers as powers of a number, or base number systems, is very useful for both representing numbers and performing arithmetic operations.
- The concept of a base number system marked a significant change in the history of number systems.
- Our current Hindu number system is based on this structure.
Abacus that Makes Use of the Decimal System
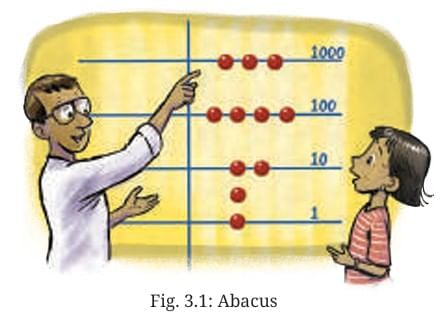
- In the 11th century, even those who still used Roman numerals began to use a calculating tool called the abacus, which was built on the decimal system.
- The abacus was a board with lines, where each line represented a power of 10.
- Numbers were represented by grouping them into landmark numbers (powers of 10), similar to how they have been grouped previously.
- For each power of 10, counters were placed on the corresponding line based on how many times that power occurred.
- A counter placed above a line contributed a value of 5.
- For instance, the number 3426 can be grouped as follows: 3426 = 1000 + 1000 + 1000 + 100 + 100 + 100 + 100 + 10 + 10 + 1 + 1 + 1 + 1.
- This number was represented as illustrated in the abacus.
- Notice how the 6 ones are represented.
- To understand how the abacus was used for calculations, consider a simple addition problem: 2907 + 43.
- The two numbers were placed on either side of a vertical line in the abacus.
III. Shortcomings of the Egyptian System
- The Egyptian number system allowed for relatively efficient representation of numbers up to a crore (107).
- It made calculations easier, but there was a significant drawback.
- As the need arose to represent larger numbers, an infinite number of symbols would be required for increasingly larger powers of 10.
- This highlights a recurring challenge in the representation of numbers that appears in another form.
- The next and final concept in the development of number systems addresses this issue.
- It not only solves the problem of large number representation but also greatly simplifies how numbers are represented and calculated.
Place Value Representation
I. The Mesopotamian Number System

- Initially, the Mesopotamian number system had different symbols for different landmark numbers.
- Later, it evolved into a base-60 system, also known as the sexagesimal system, which was very efficient.
- The choice of base 60 is debated, with theories ranging from its connection to lunar cycles to its ease of representing fractions.
- The influence of this system is still seen in our time measurements (1 hour = 60 minutes, 1 minute = 60 seconds).
- This system used a symbol
 for 1 and
for 1 and  for 10.
for 10. - Numbers from 1 to 59 could be represented using combinations of these symbols.
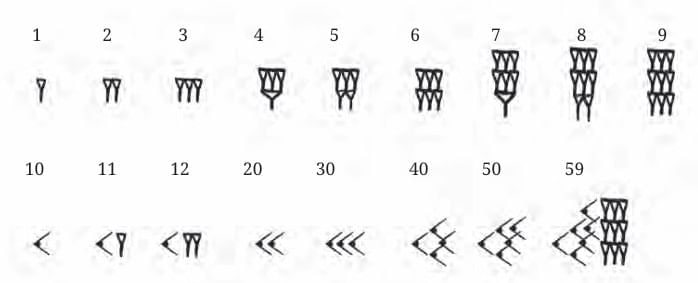
- For example, 640 was represented as (10) × 60 + 40.
- In a more compact form, they would represent it by placing the symbols for 10 and 40 next to each other, where the position indicated the power of 60.
- What made the Mesopotamian system revolutionary was its use of place value.
- The rightmost set of symbols represented 1s, the next to the left represented 60s, then 3600s, and so on.
- A blank space indicated the absence of a power of 60.
- This removed the need for an unending sequence of symbols for landmark numbers.
- This idea of place value is a major breakthrough in the history of number systems, offering an elegant solution to representing an unending sequence of numbers with a finite set of symbols.
- However, the Mesopotamian system was not a fully developed place value system.
- It had ambiguities due to inconsistent spacing for blanks, making it difficult to distinguish numbers like 60 from 3600.
- Later Mesopotamians introduced a 'placeholder' symbol for blank spaces, similar to our 0.
- This made the system unambiguous.
- However, this placeholder was mainly used in the middle of numbers, not at the end, leading to some remaining ambiguities.
II. The Mayan Number System

- The Mayan civilization in Central America developed its own place value system independently.
- They also used a placeholder symbol for zero, which looked like a seashell.
- Their system was primarily base-20, but with a puzzling third landmark number of 360 instead of 400, possibly related to their calendar.
- They used a dot for 1 and a bar for 5, combining them to represent numbers from 1 to 19.
- The symbols for different landmark numbers were written vertically, with the lowest set representing 1s, the next 20s, then 360s, and so on.
- Despite its place value notation and use of a zero placeholder, the Mayan system was not a true base-20 system, limiting its advantages for computations.
- Nevertheless, its independent development of place value and zero is a significant advance.
- Interestingly, base-20 counting can still be found in some European languages.

III. The Chinese Number System

- The Chinese used two number systems: a written system and a rod-based system for computations.
- The rod numerals, developed by at least the 3rd century AD and used until the 17th century, were more efficient.
- This was a decimal (base-10) system with specific symbols for 1 to 9.
- Similar to the Mesopotamians, rod numerals used blank spaces to indicate skipped place values.
- However, due to more uniform symbol sizes, these blanks were easier to locate.
- The Chinese system, with a symbol for zero, would be a fully developed place value system.

IV. The Hindu Number System
The Hindu/Indian number system is a base-10 (decimal) place value system that uses ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Each digit's position determines its value (e.g., in 375, 3 is in the hundreds place, 7 in the tens, and 5 in the ones).
The Hindu number system has had a symbol for 0 since at least 200 BCE. The use of 0 as a digit and the single-digit representation in each position eliminate ambiguity in reading and writing numbers. This is why it is now used worldwide.
The introduction of 0 as a digit and a number was a breakthrough. In Indian mathematics, 0 was not just a placeholder but a number in its own right. Aryabhata (499 CE) used its arithmetic properties for computations. Brahmagupta (628 CE) codified 0 as a number on which basic arithmetic operations could be performed, creating the concept of a 'ring' (a set of numbers closed under addition, subtraction, and multiplication). These ideas laid the foundation for modern mathematics, especially algebra and analysis.
This history shows the evolution of ideas in number representation:
- Counting in groups of a single number: (e.g., Gumulgal's ukasar-ukasar-urapon)
- Grouping using landmark numbers: (e.g., Roman numerals I, V, X, L, C, M)
- Choosing powers of a number as landmark numbers (the idea of a base): (e.g., 1, 101, 102, 103...)
- Using positions to denote landmark numbers (the idea of place value system): (e.g., 1729 where position matters)
- The idea of 0 as a positional digit and as a number.
The discovery of 0 and the resulting Indian number system is one of the greatest inventions, constantly appearing in our daily lives and forming the basis of modern science, technology, computing, accounting, and surveying.

|
13 videos|110 docs|11 tests
|
FAQs on A Story of Numbers Chapter Notes - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are some of the earliest number systems used by humans? |  |
| 2. How does the idea of a base influence number systems? |  |
| 3. What is place value representation, and why is it important? |  |
| 4. Can you explain how different cultures approached numbers historically? |  |
| 5. What is the significance of solved examples in understanding number systems? |  |















