A Square And A Cube Chapter Notes | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
| Table of contents |

|
| Introduction |

|
| Square Numbers |

|
| Patterns and Properties of Perfect Squares |

|
| Perfect Squares and Odd Numbers |

|
| Square Roots |

|
| Cubic Numbers |

|
| Taxicab Number |

|
| A Pinch of History |

|
| Solved Examples |

|

Introduction
Mathematics often hides itself in stories and puzzles, making numbers come alive in unexpected ways. In this chapter, we begin with the tale of Queen Ratnamanjuri, who left behind not only her fortune of precious stones but also a clever puzzle for her son Khoisnam and their 99 relatives. The puzzle involved 100 lockers and a set of rules for opening and closing them. At first, the task seemed confusing, but Khoisnam quickly realised that the answer lay in understanding factors and their patterns.
Through this story, we discover why certain lockers remain open and others close, leading us to the fascinating world of square numbers. We learn that lockers corresponding to square numbers (like 1, 4, 9, 16, …) stay open because these numbers have an odd number of factors. This insight introduces us to the concept of squares and cubes—numbers formed by multiplying a number by itself or by itself twice.
Square Numbers
1. Understanding Squares
Square numbers come from the area of a square.
The area of a square is found by multiplying its side by itself.
Area of square = Side x Side
For example:
If the side of a square is 1 unit, the area = 1 × 1 = 1.
If the side is 2 units, the area = 2 × 2 = 4.
If the side is 3 units, the area = 3 × 3 = 9.

This is why numbers like 1, 4, 9, 16, … are called square numbers.
Notation for Squares
A square number is a number that can be expressed as the product of a number with itself. For any number n, its square is written as n² (read as 'n squared').
Examples:
- 1 x 1 = 1² = 1
- 2 x 2 = 2² = 4
- 3 x 3 = 3² = 9
Can we have a square of side lengthor 2.5 units?
Yes, there area in square units are,
and (2.5)² = (2.5) × (2.5) = 6.25.
Patterns and Properties of Perfect Squares
First, let’s calculate the squares of the first 30 natural numbers (natural numbers are counting numbers starting from 1). 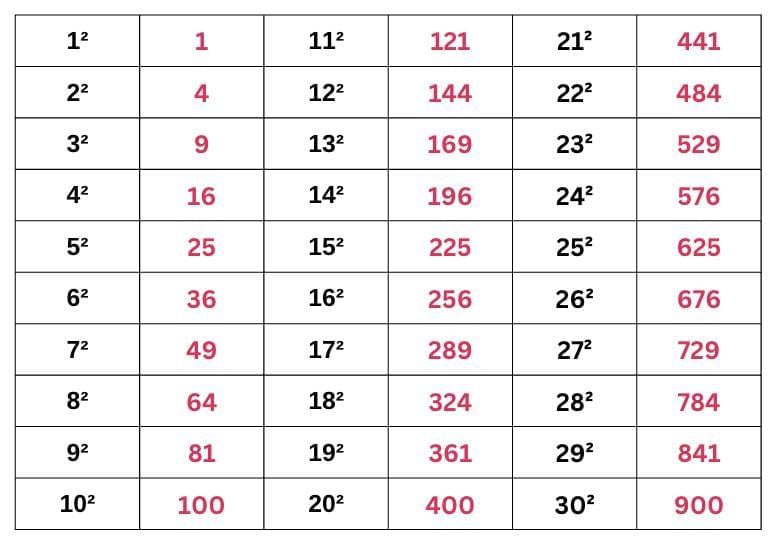
Let’s Explore the Patterns in Square Numbers
1. Units Digit of Square Numbers
Let’s study the unit digit (the digit in the ones place) of square numbers.
Look at the last digit (units place) of square numbers.
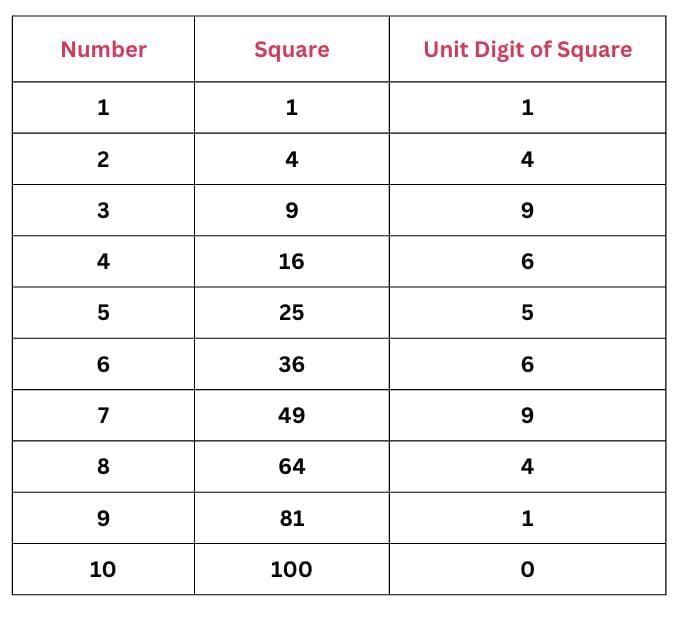
The units digit of a square can only be: 0, 1, 4, 5, 6, or 9.
A square never ends with 2, 3, 7, or 8.
Example:
16, 25, 49, 81 → all are squares.
12, 23, 57, 68 → cannot be squares.
Quick check rule: If a number ends with 2, 3, 7, or 8, it is not a square.

Example:
- 16 and 36 are square numbers that end in 6.
- But 26 also ends in 6, and 26 is NOT a square.
So, unit digit can help us rule out non-squares, but it cannot confirm a square.
Example: Write five numbers that are not squares just by looking at the units digit.
Solution:
- 23 → ends in 3 → not a square
- 47 → ends in 7 → not a square
- 58 → ends in 8 → not a square
- 132 → ends in 2 → not a square
- 703 → ends in 3 → not a square
2. Patterns with Units Digits
a) Pattern with Squares Ending in 1
If a number ends in 1 or 9, its square ends in 1.
Examples:
1² = 1→ ends in 1
9² = 81→ ends in 1
11² = 121→ ends in 1
19² = 361→ ends in 1
29² = 841→ ends in 1
b) Pattern with Squares Ending in 6
If a number ends in 4 or 6, its square ends in 6.
Examples:
4² = 16→ ends in 6
6² = 36→ ends in 6
14² = 196→ ends in 6
26² = 676→ ends in 6
3. Number of Zeros at the End
If a number ends with n zeros, its square ends with 2n zeros.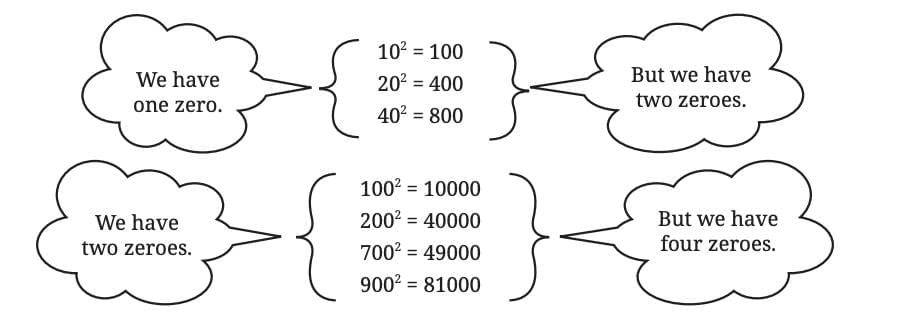
(a) If a number has 1 zero at the end → 2 x 1 = 2 zeros
Example: 10² = 100
(b) If a number has 2 zeros → 2 x 2 = 4 zeros
Example: 100² = 10,000
(c) If a number has 3 zeros → 2 x 3 = 6 zeros
Example: 1000² = 1,000,000
Rule: A square always has an even number of zeros at the end.
4. Parity (Even/Odd Property)
(a) The square of an even number is always even.
Example:
- 2² = 4 (even)
- 4² = 16 (even)
- 12² = 144 (even)
- 20² = 400 (even)
(b) The square of an odd number is always odd.
Example:
- 1² = 1 (odd)
- 3² = 9 (odd)
- 11² = 121 (odd)
- 25² = 625 (odd)
So, the square has the same parity as the number!
Perfect Squares and Odd Numbers
When we look at consecutive square numbers, we notice that the difference between them is always an odd number.
2² – 1²
= 4 – 1
= 33² – 2²
= 9 – 4
= 54² – 3²
= 16 – 9
= 75² – 4²
= 25 – 16
= 9
From this we observe that adding consecutive odd numbers starting from 1 gives consecutive square numbers, as shown below: 
Conclusion: The sum of the first n odd numbers is always equal to n².
We can also see this in the figure given below, notice how when we add odd number of dots, they form a square.

This pattern can be explained with diagrams of squares:
Each time we build the next square, we are adding an “L-shaped strip” of dots.
That “L” shape always contains an odd number of dots (1, 3, 5, 7 …).
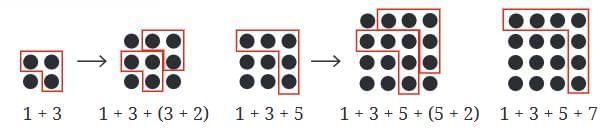
We see that the sum of the first n odd numbers is n2. Alternatively, every square is a sum of successive odd numbers starting from 1
Checking Perfect Squares by Subtracting Odd Numbers
We can test if a number is a perfect square by successively subtracting odd numbers (1, 3, 5, …).
If we reach 0, the number is a perfect square.
If we cross below 0, it is not a perfect square.
Example: Check if 25 is a perfect square.
25 – 1 = 24
24 – 3 = 21
21 – 5 = 16
16 – 7 = 9
9 – 9 = 0
→ 25 is a perfect square.
What if a Number is Not a Square?
Let’s say we take a number and try subtracting consecutive odd numbers from it:
If we couldn’t reach 0, so it is not a perfect square.
A number is a perfect square only if you can subtract consecutive odd numbers from it (starting with 1), and you end up at 0.
If you don’t reach 0, it is not a perfect square.
Example: Check 38 is a perfect square.
38 – 1 = 37
37 – 3 = 34
34 – 5 = 29... (continues)
→ does not reach 0
→ 38 is not a perfect square.
Finding the Next Square Using Odd Numbers
If you know n², then (n+1)² can be found by simply adding the next odd number.
Example: Find 36², given 35² = 1225.
The 36th odd number = 2n – 1 = 2 × 36 – 1 = 71.
So, 35² + 71 = 1225 + 71 = 1296.
Therefore, 36² = 1296.
Numbers Between Two Consecutive Squares
The number of integers between n² and (n+1)² is always 2n.
Let’s take examples:
- Between 1² = 1 and 2² = 4 → numbers are: 2 and 3 → 2 numbers
- Between 2² = 4 and 3² = 9 → numbers are: 5, 6, 7, 8 → 4 numbers
- Between 3² = 9 and 4² = 16 → numbers are: 10 to 15 → 6 numbers
- Between 4² = 16 and 5² = 25 → numbers are: 17 to 24 → 8 numbers
Pattern:
The number of values between n² and (n+1)² is always 2n. Where 'n' is the number that we are squaring
How many square numbers are there between 1 and 100?
Perfect squares between 1² = 1 and 10² = 100 are:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100
→ Total: 10 square numbers
Perfect Squares and Triangular Numbers
Triangular numbers are numbers that can be represented by a triangular grid of objects.
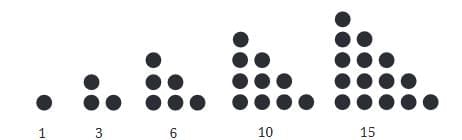
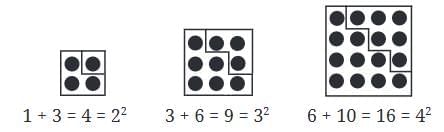
Square Roots
Imagine a square of area 49 sq. cm. What is the length of its side?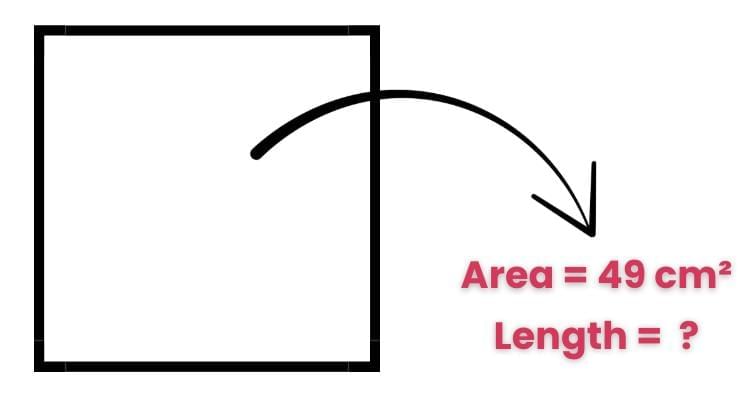 We know that Area = Side x Side = Side2
We know that Area = Side x Side = Side2
7 × 7 = 49, or 72 = 49.
So, the length of the side of a square with an area of 49 sq. cm is 7 cm.
We call 7 the square root of 49.
Definition:
If y= x2 then x is the square root of y.
The symbol of square root is: √
Example:
- 12= 1,
Therefore, √1 is 1. - 22= 4,
Therefore, √4 is 2. - 32= 9,
Therefore, √9 is 3.
Note: Every perfect square has two integer square roots: one positive and one negative.
Notation: √n = ±x, where n = x².
Example: √64 = ±8,
But in this chapter, we will mostly work with the positive square root only.
So:
How to Check if a Number is a Perfect Square
There are 4 methods to find this, lets understand each one of them.
(i) List all the Square Numbers
We know that perfect squares can only end in certain digits: 1, 4, 5, 6, 9, or an even number of zeros.
But this rule only helps us eliminate some numbers—it doesn’t confirm a square.
For instance, it’s obvious that 327 is not a perfect square because it ends in 7.
However, a number like 576 ends in 6, so it might be a square. To be sure, we need to check further.
One method is to list nearby perfect squares.
Since 20² = 400, we check the next few squares:
21² = 441
22² = 484
23² = 529
24² = 576
Thus, 576 is indeed a perfect square.
However, this method becomes slow and impractical for very large numbers. More efficient techniques are needed to test whether big numbers are perfect squares.
(ii) By Successive Subtraction of Odd Numbers
Remember that any perfect square can be written as the sum of consecutive odd numbers starting from 1.
Example: Take the number 81 as an example:

We subtracted consecutive odd numbers beginning with 1 and reached 0 in the 9th step. This tells us that the √81 is 9.

(iii) By Prime Factorisation
A perfect square is the product of a whole number multiplied by itself.
We can check this using prime factorisation:
If the prime factors of a number can be grouped into pairs of identical factors, the number is a perfect square.
The product of one factor from each pair gives the square root.
Key Terms:
Prime numbers: Numbers greater than 1 that are divisible only by 1 and themselves.
Examples: 2, 3, 5, 7, 11Composite numbers: Numbers that can be divided by numbers other than 1 and themselves.
Examples: 6, 8, 12, 15Prime factorisation: Writing a composite number as a product of prime numbers.
For example, let's find the square root of 256:
- The prime factorisation of 256 is 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2.
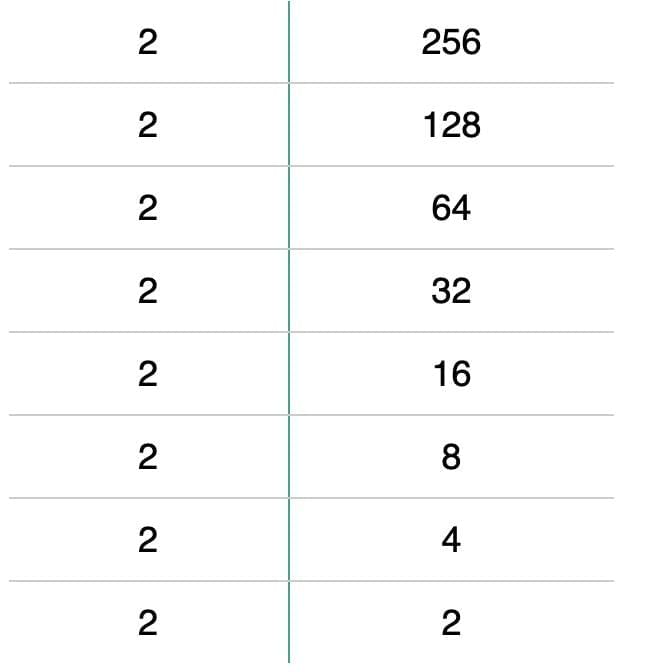
- Pairing the prime factors, we have 256 = (2 × 2) × (2 × 2) × (2 × 2) × (2 × 2) = (2 × 2 × 2 × 2)
- Therefore, the square root of 256 is 2 × 2 × 2 × 2 = 16.
Ques: Is 324 a perfect square?
 View Answer
View Answer 
Solution: 324 = 2 × 2 × 3 × 3 × 3 × 3. 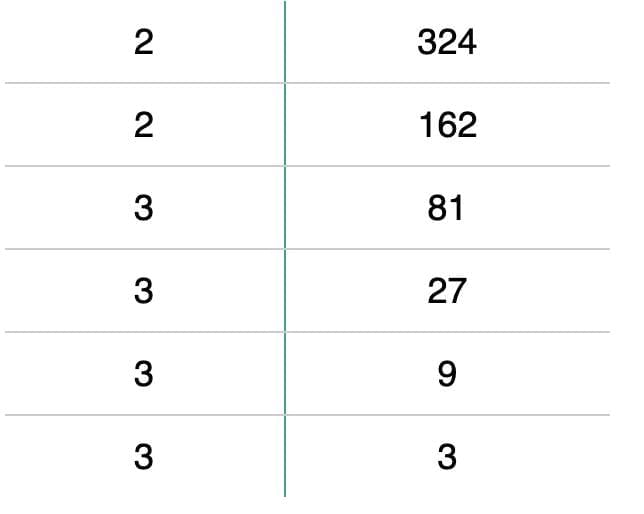 These can be grouped as 324 = (2 × 2) × (3 × 3) × (3 × 3). = 22 × 32 × 32 = 182.
These can be grouped as 324 = (2 × 2) × (3 × 3) × (3 × 3). = 22 × 32 × 32 = 182.
We can also write the prime factors in pairs.
That is, 324 = 22 × 32 × 32, which shows that 324 is a perfect square.
Thus, 324 = (2 × 3 × 3)2 = 182. Therefore, 324 =18.
(iv) Estimating Square Roots
(a) For perfect Square Roots
For large numbers that are not obvious squares, we estimate by finding two perfect squares close to the given number. The square root will lie between them.
Example: Let’s try to find the square root of 1936.
Step 1: Find two perfect squares between which 1936 lies.
We know:
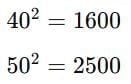
So, 1936 lies between 1600 and 2500.
This means:
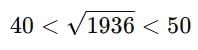
Step 2: Look at the last digit.
The last digit of 1936 is 6.
Perfect squares that end in 6 usually come from numbers ending in 4 or 6 (since 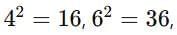 etc.)
etc.)
So the square root of 1936 might end in 4 or 6. That means it could be 44 or 46.
Step 3: Try one of the guesses.
Let’s try :
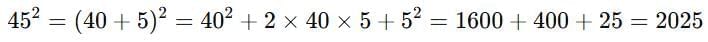 But 2025 is more than 1936.
But 2025 is more than 1936.
So, the square root must be less than 45. That narrows it to:
Step 4: Verify 44
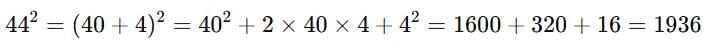
Perfect!
So,
(b) For Non-Square Roots
Consider the following situation — Aribam and Bijou play a game.
One says a number and the other replies with its square root. Aribam starts. He says 25, and Bijou quickly responds with 5. Then Bijou says 81, and Aribam answers 9. The game goes on till Aribam says 250. Bijou is not able to answer because 250 is not a perfect square. Aribam asks Bijou if he can at least provide a number that is close to the square root of 250.
How Can Bijou Estimate √250?
Let’s think step by step:
Find two perfect squares around 250:
- So we know: 100 < 250 < 400 and √100 = 10, √400 = 20
- So, 10 < √250 < 20
- But, we are still very far away from the number whose square is 250
Get closer:
- So: 15 < √
Which is it closer to?
250 is closer to 256 than 225.
250 lies between 225 and 256, closer to 256
→ √250 ≈ 15.8 (slightly less than 16).
Cubic Numbers
In geometry, a cube is a solid shape where all sides are equal and all angles are right angles.
 Cube
Cube
Now, think of a cube with side 2 cm. How many 1 cm³ cubes fit inside it?
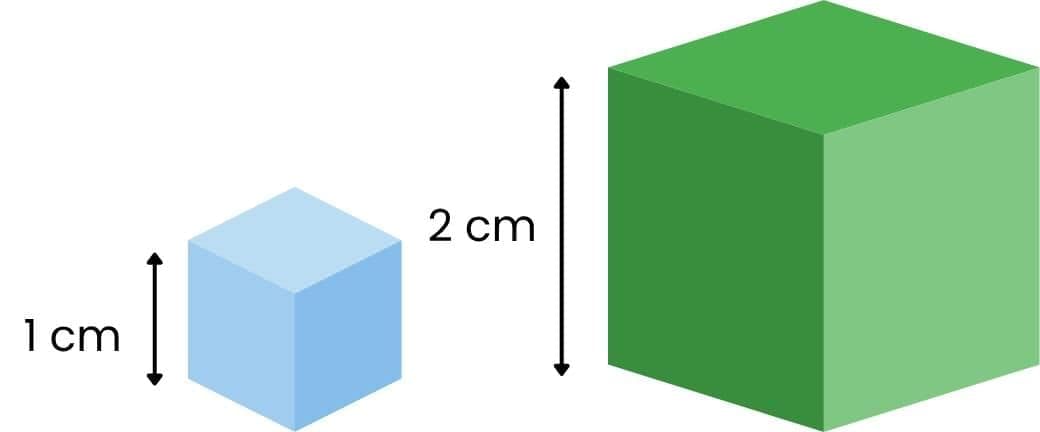
- Volume of big cube = cm³
- Volume of small cube = cm³
- Number of small cubes =
So, 2³ = 8. That’s why we call 8 a cubic number—it’s the cube of 2.
Try with 3 cm:
Volume = cm³ → 3³ = 27
A cubic number shows how many unit cubes fit inside a cube of side n.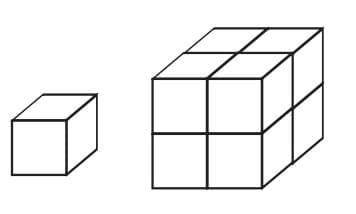
Definition of a cubic number:
A cubic number (or perfect cube) is obtained by multiplying a number by itself three times. For any number n, its cube is written as n³.
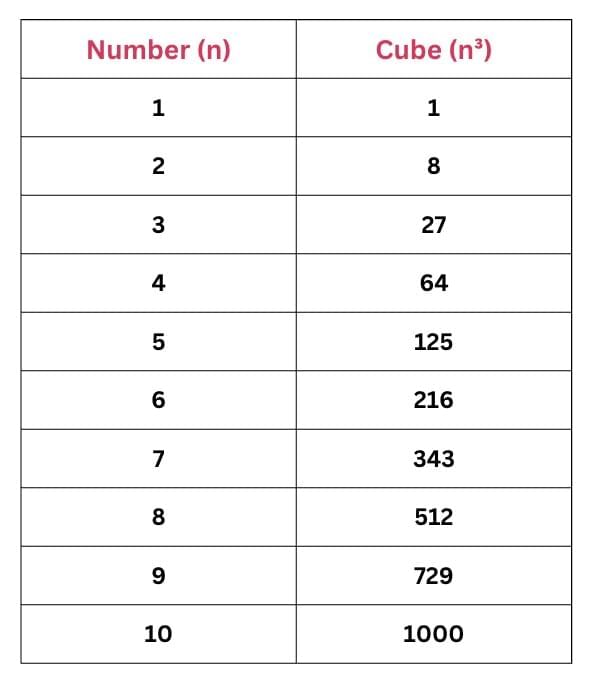
These are called Cube Numbers because each of these numbers can be used to form a cube with equal-length sides using unit cubes (1 cm³)
Observation: A cube grows much faster than a square as the number increases.
Patterns in Cubes
The last digit of a square can only be 0, 1, 4, 5, 6, or 9.
The possible last digits of cubes are 0, 1, 4, 5, 6, 9, 8, 7, 3, 2 (all digits except some repeated restrictions).
Just as we can take squares of fractions/decimals 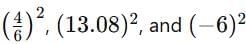 we also can compute cubes of such numbers
we also can compute cubes of such numbers
Taxicab Number
Once, a great mathematician named Srinivasa Ramanujan was sick and staying in a hospital in England.
Another famous mathematician, G. H. Hardy, came to visit him. Hardy told Ramanujan that he came in a taxi numbered 1729. He said the number looked boring and hoped it wasn’t a bad sign.
Ramanujan replied immediately,
“No, Hardy, it is a very interesting number.”
He explained that 1729 is special because:
This means that 1729 is the smallest number that can be written as the sum of two cube numbers in two different ways.
After this conversation, the number 1729 became famous and is now called the Hardy-Ramanujan Number.
What Is a Taxicab Number?
Numbers that can be written as the sum of two cube numbers in two different ways are called Taxicab Numbers.
For example:
1729 = 1³ + 12³ = 9³ + 10³
4104 = 2³ + 16³ = 9³ + 15³
13832 = 2³ + 24³ = 18³ + 20³
You can try checking these using a calculator.
How Did Ramanujan Know This?
Ramanujan loved numbers deeply. He would spend hours playing with and studying them.
His friends often said that he could see beautiful patterns in numbers that no one else noticed.
One of his colleagues, John Littlewood, even said:
“Every positive number was one of Ramanujan’s personal friends.”
This means that numbers weren’t just symbols to Ramanujan—they felt alive and full of meaning to him.
Perfect Cubes and Consecutive Odd Numbers
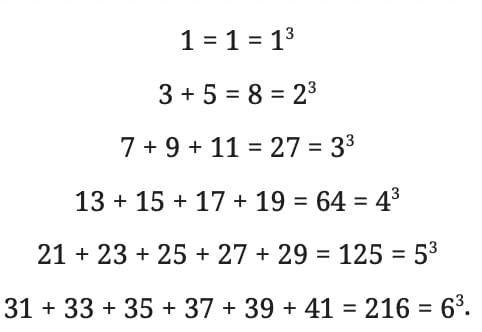
General Pattern:
The sum of n consecutive odd numbers, starting from a certain point, equals n³.
Example:
4³ = 64 = 13 + 15 + 17 + 19 (4 odd numbers)
6³ = 216 = 31 + 33 + 35 + 37 + 39 + 41 (6 odd numbers)
Further Example:
91 + 93 + 95 + 97 + 99 + 101 + 103 + 105 + 107 + 109 = 1000 = 10³
Cube Roots
We know that: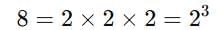 This means that 2 is the cube root of 8.
This means that 2 is the cube root of 8.
We write this as: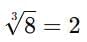 This special symbol —
This special symbol —  — is read as “cube root.”
— is read as “cube root.”
Definition
If:
Then:
In simple words:
If a number y is made by multiplying x × x × x,
Then x is the cube root of y.
Finding Cube Roots Using Prime Factorisation
Example: Is 3375 a perfect cube?
Sol: Let’s break 3375 into prime factors:
We can group the factors into three identical groups:
(3×5), (3×5), (3×5)
So, it is a perfect cube
Another Way (Grouping into Triplets):
You can also check by grouping same factors into sets of three:
So, 3375 is a perfect cube and its cube root is 15.
Example : Find if 8000 is a perfect cube or not.
Sol: Prime factorization of 8000
= 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5
So,
= 2 × 2 × 5 = 20
So, 8000 is a perfect cube
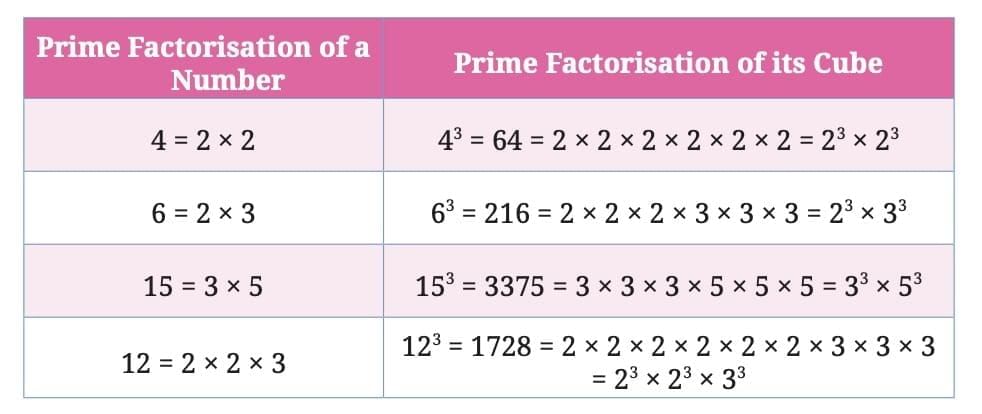
Observe that each prime factor of a number appears three times in the prime factorisation of its cube.
Successive Differences
You've already seen how perfect squares show a pattern when we calculate successive differences.
Let’s recall:
Perfect Squares:
1, 4, 9, 16, 25, 36
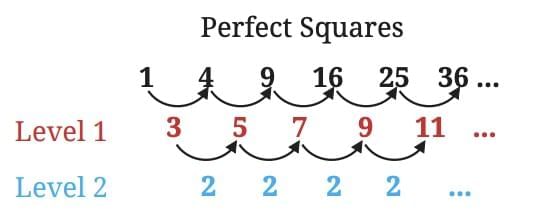
So, after two levels of differences, we get a constant value. That tells us that perfect squares settle into a fixed pattern at Level 2.
Now let’s try the same for perfect cubes.
Perfect Cubes:
1, 8, 27, 64, 125, 216
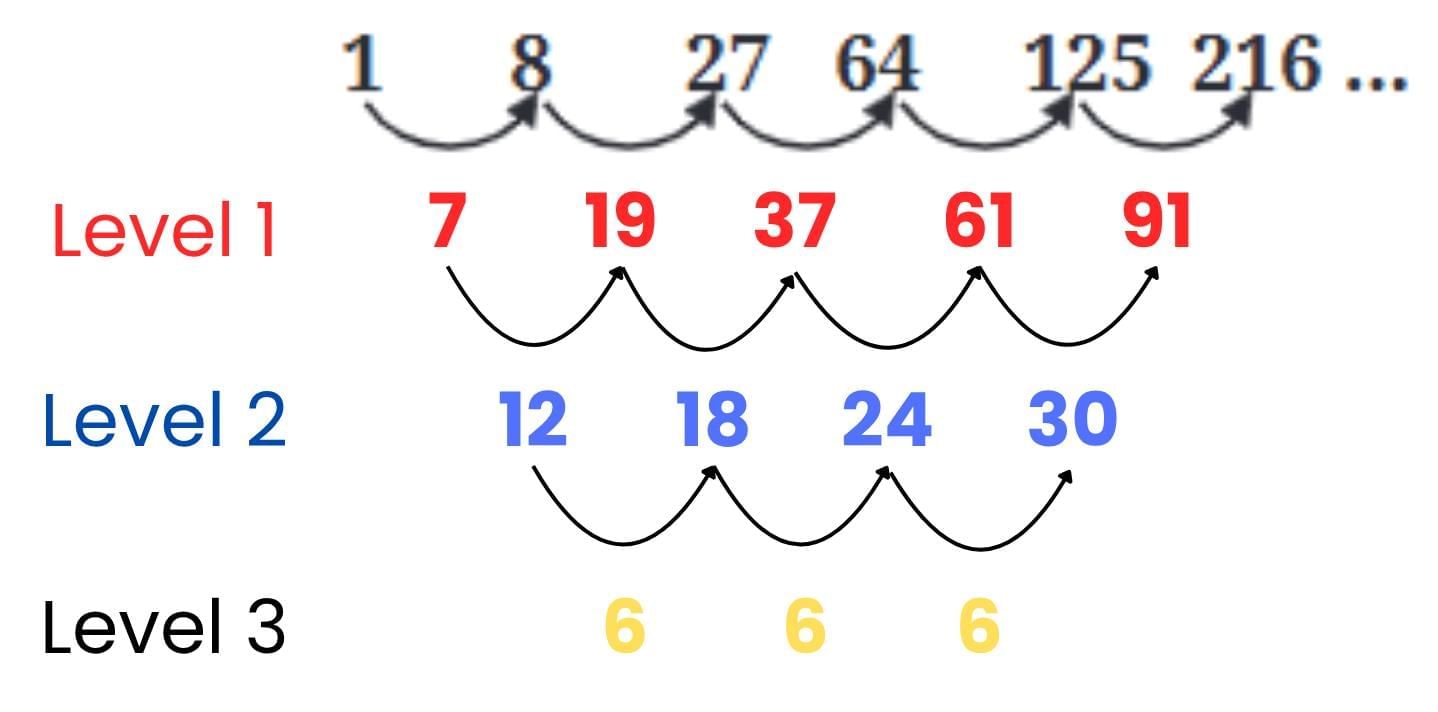
What do we observe?
For squares → constant differences appear at the second level.
For cubes → constant differences appear at the third level.
General Rule:
For powers of numbers:
Differences of squares (n²) become constant at level 2.
Differences of cubes (n³) become constant at level 3.
In general, differences of n-th powers become constant at level n.
A Pinch of History
Ancient Records
- The Babylonians, around 1700 BCE, made the first known lists of perfect squares (like 1, 4, 9, 16) and perfect cubes (like 1, 8, 27, 64).
- These lists were written on clay tablets.
- They used them to quickly find square roots and cube roots, especially in solving problems related to land measurement, building design, and other geometric calculations.
 Clay tablets used by Babylonians
Clay tablets used by Babylonians
Use in Ancient India
In Sanskrit (an ancient Indian language), certain words were used for these concepts:
- Varga meant both a square shape and square of a number.
- Ghana meant both a solid cube and the cube of a number (number multiplied by itself three times).
- Varga-varga referred to the fourth power (square of a square).
- These words were used in India as early as the third century BCE.
Aryabhata's Definition (499 CE)
Aryabhata, a famous Indian mathematician, explained:
- A square figure (having 4 equal sides) and the number representing its area are both called varga.
- The product of two equal numbers (like 5 × 5) is also called varga.
Why the Word "Root"?
In ancient India, the Sanskrit word mula was used. It means:
- Root of a plant, basis, origin, or cause.
- In mathematics, varga-mula meant the square root and ghana-mula meant the cube root.
- The idea was: Just as a plant grows from its root, a square grows from its square root.
- This idea of "root" for mathematical operations was later used in Arabic (word: jidhr) and Latin (word: radix), both meaning “root of a plant”.
Another Word: Pada
- The word pada, which means foot, base, or origin, was also used in Sanskrit.
- The mathematician Brahmagupta (628 CE) said:
- The pada (root) of a krti (square) is the number that was squared to get it.
Solved Examples
- Solution: We use prime factorization.
196 = 2 x 98
= 2 x 2 x 49
= 2 x 2 x 7 x 7
Group the factors into pairs: (2 x 2) x (7 x 7)
Take one factor from each pair and multiply: 2 x 7 = 14
Therefore, the square root of 196 is 14.
- Solution: We find the prime factors of 243.
243 = 3 x 81 = 3 x 3 x 27
= 3 x 3 x 3 x 9
= 3 x 3 x 3 x 3 x 3
The prime factors are (3 x 3) x (3 x 3) x 3.
Since the factor 3 is left over and cannot be paired, 243 is not a perfect square.
- Solution: We use prime factorization.
1728 = 2 x 864
= 2 x 2 x 432
= 2 x 2 x 2 x 216
= 2 x 2 x 2 x 6³
= 2 x 2 x 2 x (2x3) x (2x3) x (2x3)
= 2x2x2x2x2x2x3x3x3
Group the factors into triplets: (2 x 2 x 2) x (2 x 2 x 2) x (3 x 3 x 3)
Take one factor from each triplet and multiply: 2 x 2 x 3 = 12
Therefore, the cube root of 1728 is 12.
- Solution: Find the prime factors of 392.
392 = 2 x 196
= 2 x 2 x 98
= 2 x 2 x 2 x 49
= (2 x 2 x 2) x 7 x 7
The prime factor 2 forms a triplet, but the factor 7 only appears twice.
To make it a perfect cube, we need one more 7.
Therefore, the smallest number to multiply by is 7.
- Solution: First, find the LCM (Least Common Multiple) of 4, 9, and 10.
4 = 2 x 2
9 = 3 x 3
10 = 2 x 5
LCM = 2 x 2 x 3 x 3 x 5 = 180
Now, find the prime factors of the LCM: 180 = 2 x 2 x 3 x 3 x 5.
To make it a perfect square, all factors must be in pairs.
The factor 5 is not in a pair. So, we need to multiply by 5. 180 x 5 = 900
Therefore, the smallest square number divisible by 4, 9, and 10 is 900.
|
13 videos|110 docs|11 tests
|
FAQs on A Square And A Cube Chapter Notes - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are cubic numbers and how are they defined? |  |
| 2. How can we find the cubic numbers between specific limits? |  |
| 3. What is the relationship between square numbers and cubic numbers? |  |
| 4. Can a number be both a square and a cubic number? |  |
| 5. How are cubic numbers used in real-world applications? |  |
















