Case Based Questions: Electricity | Science Class 10 PDF Download

Q1: Read the source below and answer the questions that follow:

Ohm's law gives a relationship between current and potential difference. According to this law, at constant temperature, the current flowing through a conductor is directly proportional to the potential difference across its ends. The ratio of potential difference applied between the ends of a conductor and the current flowing through it is a constant quantity called resistance. The following graph is obtained by a researcher while doing an experiment to study Ohm's law. The I-V graph for four conductors A, B, C and D having resistances RA, RB, RC and RD respectively are shown in the graph.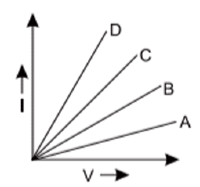 

i. If all the conductors are of same length and same material, which is the thickest? (1 mark)
(a) C 
(b) D 
(c) A 
(d) B 
ii. If all the conductors are of same thickness and of same material, which is the longest? (1 mark)
(a) B 
(b) C 
(с) А 
(d) D 
iii. Which one of the following relations is true for these conductors? (1 mark)
(a) RA > RB >RC> Ro
(b) RA=RB < Rc <Ro 
(c) R_A < R_B < R_c <R_o
(d) R_A = R_B=R_C=R_{o
iv. If conductors A and B are connected in series and I-V graph is plotted for the combination, its slope would be: (1 mark)
(a) more than that of A 
(b) between A and B 
(c) more than that of D 
(d) less than that of A
Or
iv. If conductors C and D are connected in parallel and I-V graph is plotted for the combination, its slope would be: (1 mark)
(a) between C and D 
(b) lesser than that of A 
(c) more than that of D 
(d) between B and C}  

_{Ans:
i. (b) D 
ii. (c) A 
iii. (a) RARB>RC>Ro 
iv. (d) less than that of A 
v. (c) more than that of D} 

_{Q2: Read the source below and answer the questions that follow:}

Vinita and Ahmed demonstrated a circuit that operates the two headlights and the two sidelights of a car, in their school exhibition.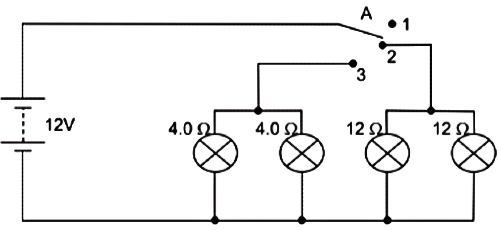
i. State what happens when switch A is connected to (1 mark)
(a) Position 2 
(b) Position 3 
ii. Find the potential difference across each lamp when lit. (1 mark)
iii. Calculate the current: 
(a) In each 12Ω lamp when lit. 
(b) In each 4 Ω lamp when lit. 
iii. Show, with calculations, which type of lamp, 4.0 Ω or 12 Ω has the higher power. (1 mark)

Ans:
i. (a) Only 12 2 lamps will light up. 
(b) Only 4 lamps will light up. 
ii. 12 V for both sets of lamps as all of them are in parallel. 
iii. (a) Voltage across both 12 2 lamps = 12 V.
Using Ohm's law, V = IR
I = V / R = 12 / 12 = 1 A
(b) Voltage across both 4Ω lamps = 12 V.
Using Ohm's law, V = IR.
I = V / R = 12 / 4 = 3 A.
iv. All lamps are in parallel and hence same V for all lamps.
Using, P = V² / R
For 4Ω lamps, P = 12 × 12 / 4 = 36 W
For 12Ω lamps, P = 12 × 12 / 12 = 12 W
Hence, 4Ω lamps will have higher power.

Q3: Read the source below and answer the questions that follow:

When an electric current passes through a conductor (like a high resistance wire) the conductor becomes hot after some time and produces heat. This is called heating effect of electric current or joule heating or ohmic heating or resistive heating. The heating effect of electric current is widely used in our day- to-day life. The electric laundry iron, electric toaster, electric bulb, fuse and electric heater are some of the familiar devices based on Joule's heating. 

i. Write the mathematical expression for Joule's law of heating. (1 mark)
ii. The following table gives the resistivity of three samples: (1 mark)
Which of them is suitable for heating elements of electrical appliances and why? 
iii. Why does the cord of an electric heater not glow while the heating element does? (1 mark)
iv. State a difference between the wire used in the element of an electric heater and in a fuse wire. (1 mark)
Or
iv. Tungsten is used almost exclusively for filaments of electric bulb. List two reasons. (1 mark)

Ans:
i. The mathematical expression for Joule's law of heating is: Heat generated, H=12Rt where is the amount of current flowing through the conductor, R is the resistance of conductor and t is the time for which the current has flown. 
ii. The resistivity of sample C is maximum so it is suitable for making heating elements of electrical appliances. 
iii. The cord of an electric heater is made up of copper with very low resistance whereas heating elements are made up of alloys which have very high resistance. So, when current flows through the heating element, it becomes too hot and glows red due to heating effect of current. iv. The wire used in element of electric heater has high resistance and high melting point whereas a fuse wire has low resistance and low melting point.
Or
iv. Tungsten is used for making filaments of electric bulb because of the following reasons: 
(a) It has very high melting point 
(b) It has high resistivity 

Q4: Read the source below and answer the questions that follow:

Study the following electric circuit in which the resistors are arranged in three arms A, B and C:
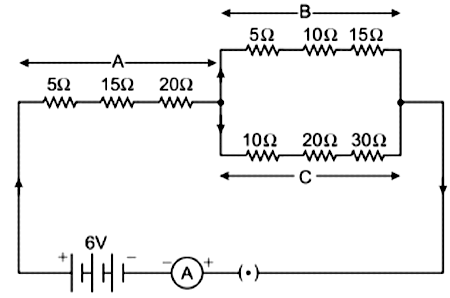i. Find the equivalent resistance of arm C. (1 mark)
ii. Calculate the equivalent resistance of the parallel combination of the arms B and C. (1 mark)
iii. Determine the current that flows through the ammeter. (1 mark)
iv Determine the current that flows in the ammeter when the arm B is withdrawn from the circuit. (1 mark)
Ans:
i. In arm C, 10 Ω, 20 Ω and 30 Ω are in series, Thus, the equivalent resistance, Rc 10+20+30=60 Ω 
ii. From the given circuit, the equivalent resistance of parallel combination of arm B and C,
1 / R_BC = 1 / (5 + 10 + 15) + 1 / (10 + 20 + 30)
= 1 / 30 + 1 / 60
1 / R_BC = 2 + 1 / 60 = 3 / 60
R_BC = 60 / 3 = 20 Ω
iii. From the given circuit, the equivalent resistanc of arm A (RA) is combined in series with R_BC .. Total resistance of the circuit R=R_A + R_BC = (5 + 15 + 20) + 20 
= 40 + 20 = 60Ω 
Thus, the current flowing through ammeter,
I = V / R = 6 / 60
= 1 / 10 = 0.1 A
iv. When the arm B is withdrawn from the circuit, the equivalent resistance,
R = (5 + 15 + 20) + (10 + 20 + 30)
= 40 + 60 = 100
∴ Current, I = V / R = 6 / 100 = 0.06 A

Q5: Read the source below and answer the questions that follow:

Consider the following electrical circuit diagram in which nine identical resistors of 3Ω each are connected as shown. The reading of the ammeter A₁ is 1 ampere.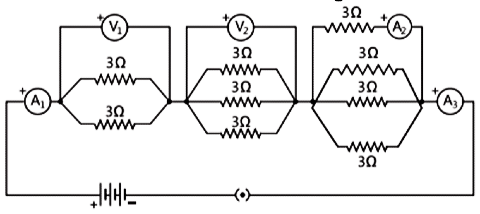
i. What is the relationship between the readings of A₁ and A3? Give reasons for your answer. (1 mark)
ii. What is the relationship between the readings of A₂ and A3? (1 mark)
iii. Determine the reading of the voltmeter V1. (1 mark)
iv. Find the total resistance of the circuit. (1 mark)

Ans:
i. Reading of A₁ = Reading of A3 because they are connected in series
ii. Reading of A₂ < Reading of A₃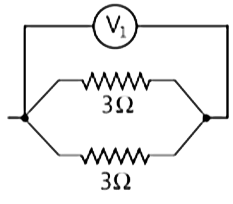
iii. 1 / Rₑq = 1 / 3 + 1 / 
or, Rₑq = 3/2 Ω = 1.5 Ω
V₁ = I Rₑq = 1 × 3/2 = 1.5 V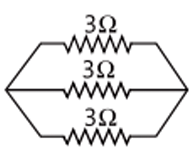
iv. 1 / Rₑq = 1 / 3 × 1 / 3 × 1 / 3 = 3 / 3 = 1
or, Rₑq = 1 Ω
Similarly, 1 / Rₑq = 1 / 3 + 1 / 3 + 1 / 3 = 4 / 3
or, R''ₑq = 3 / 4 Ω = 0.75 Ω
Total resistance = Rₑq + Rₑq + R''ₑq
= 1.5 Ω + 1 Ω + 0.75 Ω
= 3.25 Ω

Q6: Read the source below and answer the questions that follow:

The rate of flow of charge is called electric current. The SI unit of electric current is Ampere (A). The direction of flow of current is always opposite to the direction of flow of electrons in the current.
The electric potential is defined as the amount of work done in bringing a unit positive test charge from infinity to a point in the electric field. The amount of work done in bringing a unit positive test charge from one point to another point in an electric field is defined as potential difference.
VAB = VB - VA = WBA / q
The SI unit of potential and potential difference is volt.

i. The 2 C of charge is flowing through a conductor in 100 ms, the current in the circuit is (1 mark)
(a) 20 A
(b) 2 A
(c) 0.2 A
(d) 0.02 A
ii. Which of the following is true? (1 mark)
(a) Current flows from positive terminal of the cell to the negative terminal of the cell outside the cell
(b) The negative charge moves from lower potential to higher potential.
(c) The direction of flow of current is same as the direction of flow of positive charge.
(d) All of these
iii. The potential difference between the two terminals of a battery, if 100 joules of work is required to transfer 20 coulombs of charge from one terminal of the battery to the other is (1 mark)
(a) 50 V
(b) -5 V
(c) 0.5 V
(d) 500 V
iv. The number of electrons flowing per second in a conductor if 1 A current is passing through it (1 mark)
(a) 6.25 × 10²⁰
(b) 6.25 × 10¹⁹
(c) 6.25 × 10¹⁸
(d) 6.25 × 10⁻¹⁹
Or
iv. The voltage can be written as (1 mark)
(a) Work done × charge × time
(b) Work done / Current × time
(c) Work done × time / Current
(d) Work done / charge

Ans:
i. (a) q = 2 C, t = 100 ms = 0.1 s
I = q / t = 2 / 0.1 = 20 A.
ii. (d)
iii. (b) W = 100 J, q = 20 C
V = W / q = 100 / 20 = 5 V
iv. (c) I = 1 A, t = 1 s
q = It = 1 × 1 = 1 C
= q / e = 1 / 1.6 × 10⁻¹⁹ = 6.25 × 10¹⁸
v. (c) V = W / q = W / It

Q7: Read the source below and answer the questions that follow:

The relationship between potential difference and current was first established by George Simon Ohm called Ohm’s law. According to this law, the current through a metallic conductor is proportional to the potential difference applied between its ends, provided the temperature remains constant i.e. I ∝ V or V = IR; where R is constant for the conductor and it is called resistance of the conductor. Although Ohm’s law has been found valid over a large class of materials, there do exist materials and devices used in electric circuits where the proportionality of V and I does not hold.

i. If both the potential difference and the resistance in a circuit are doubled, then (1 mark)
(a) current remains the same
(b) current is doubled
(c) current is halved
(d) current is quadrupled
ii. For a conductor, the graph between V and I is there. Which one is the correct? (1 mark)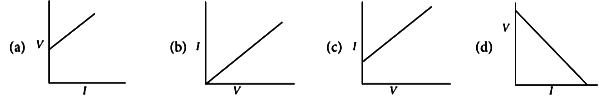
iii. The slope of V - I graph (V on x-axis and I on y-axis) gives (1 mark)
(a) resistance
(b) reciprocal of resistance
(c) charge
(d) reciprocal of charge
iv. When battery of 9 V is connected across a conductor and the current flows is 0.1 A, the resistance is (1 mark)
(a) 9 Ω
(b) 0.9 Ω
(c) 90 Ω
(d) 900 Ω
Or
iv. By increasing the voltage across a conductor, the (1 mark)
(a) current will decrease
(b) resistance will increase
(c) current will increase
(d) resistance will decrease

Ans:
i. (a) V = IR
So, V → 2 V, R' → 2R
I' = 2V / 2R = I
ii. (b) V ∝ I. So, the graph is a straight line and passing through origin.
iii. (b) Slope of V-I graph = I / V = 1 / R
iv. (c) Given: V = 9 V, I = 0.1 A
R = (V / I) = 9 / 0.1 = 90 Ω
Or
iv. (c) On increasing the voltage, the resistance remains the same, so current will increase.

Q8: Read the source below and answer the questions that follow:

The obstruction offered by a conductor in the path of flow of current is called resistance. The SI unit of resistance is ohm (Ω). It has been found that the resistance of a conductor depends on the temperature of the conductor. As the temperature increases, the resistance also increases. But the resistance of alloys like mangnin, constantan, and nichrome is almost unaffected by temperature. The resistance of a conductor also depends on the length of conductor and the area of cross-section of the conductor. More be the length, more will be the resistance, more be the area of cross-section, lesser will be the resistance.

i. Which of the following is not desired in material being used for making electrical wires? (1 mark)
(a) High melting point
(b) High resistance
(c) High conductivity
(d) None of these
ii. The V - I graph for two metallic wires A and B is given. What is the correct relationship between their temperatures? (1 mark)
(a) TA < TB
(b) TA > TB
(c) TA = TB
(d) none of these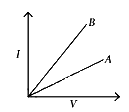
iii. Two wires of same material one of length L and area of cross-section A, other is of length 2L and area A/2. Which of the following is correct? (1 mark)
(a) R1 = R2
(b) R1 = 4R2
(c) R2 = 4R1
(d) R1 = 2R2
iv. For the same conducting wire (1 mark)
(a) resistance is higher in summer
(b) resistance is higher in winter
(c) resistance is same in summer or in winter
(d) none of these
Or
iv. A wire of resistance 20 Ω is cut into 5 equal pieces. The resistance of each part is (1 mark)
(a) 4 Ω
(b) 10 Ω
(c) 100 Ω
(d) 80 Ω

Ans:
i. (b) The electrical wire should have low resistance.
ii. (b) More is the temperature, more will be the resistance. The resistance of A is more, so temperature of A is more.
iii. (c) R₁ = ρ L / A, R₂ = ρ (2L) / (A / 2)
iv. (a) In summers, temperature is more, so resistance is more.
Or
iv. (a) R' = R / 5 = 20 / 5 = 4 Ω

Q9: Read the source below and answer the questions that follow:

Two or more resistances are connected in series or in parallel or both, depending upon whether we want to increase or decrease the circuit resistance.
The two or more resistances are said to be connected in series if the current flowing through each resistor is the same. The equivalent resistance in the series combination is given by
Rₑ = R₁ + R₂ + R₃

i. When three resistors are connected in series with a battery of voltage V and voltage drop across resistors is V₁, V₂ and V₃, which of the relation is correct? (1 mark)
(a) V = V₁ = V₂ = V₃
(b) V = V₁ + V₂ + V₃
(c) V₁ + V₂ + V₃ = 3V
(d) V > V₁ + V₂ + V₃
ii. When the three resistors each of resistance R ohm, connected in series, the equivalent resistance is (1 mark)
(a) R / 2
(b) > R
(c) < R / 2
(d) < R
iii. There is a wire of length 20 cm and having resistance 20 Ω cut into 4 equal pieces and then joined in series. The equivalent resistance is (1 mark)
(a) 20 Ω
(b) 4 Ω
(c) 5 Ω
(d) 10 Ω
iv. In the following circuit, find the equivalent resistance between A and B is (R = 2 Ω) (1 mark)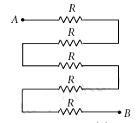
(a) 10 Ω  
(b) 5 Ω
(c) 2 Ω
(d) 4 Ω
Or
iv. In the given circuit, the current in each resistor is (1 mark)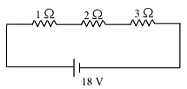

(a) 3 A
(b) 6 A
(c) 9 A
(d) 18 A

Ans:
i. (b) In series combination, the total voltage is equal to the sum of voltage drop across each resistance.
ii. (b) Rs = R1 + R2 + R3
So, Rs = R + R + R = 3R
iii. (a) Resistance of each wire = 20Ω / 4 = 5Ω
Equivalent resistance in series:
Rs = 5 + 5 + 5 + 5 = 20Ω
iv. (a) All are in series, Rs = 5R = 5 × 2 = 10Ω
Or
iv. (a): Rs = 1 + 2 + 3 = 6Ω
I = 18 / 6 = 3 A

Q10: Read the source below and answer the questions that follow:

If two or more resistances are connected in such a way that the same potential difference gets applied to each of them, then they are said to be connected in parallel. The current flowing through the two resistances in parallel is, however, not the same. When we have two or more resistances joined in parallel to one another, then the same current gets additional paths to flow and the overall resistance decreases. The equivalent resistance is given by
1 / Rp = 1 / R1 + 1 / R2 + 1 / R3
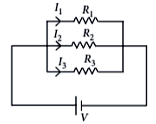i. Three resistances, 2 Ω, 6 Ω, and 8 Ω are connected in parallel, then the equivalent resistance is (1 mark)
(a) less than 6 Ω but more than 2 Ω
(b) less than 8 Ω but more than 6 Ω
(c) less than 2 Ω
(d) more than 8 Ω
ii. A wire of resistance 12 Ω is cut into three equal pieces and then twisted their ends together, the equivalent resistance is (1 mark)
(a) 3/8 Ω
(b) 4/3 Ω
(c) 3/4 Ω
(d) 5/6 Ω
iii. Three resistances are connected as shown. The equivalent resistance between A and B is______ Ω (1 mark)
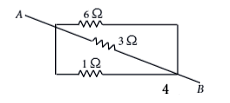(a) 2/3 Ω
(b) 3/2 Ω
(c) 4/3 Ω
(d) 3/4 Ω
iv. Which of the following relation is correct? (1 mark)
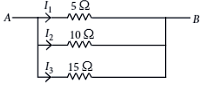(a) I₁ = 2I₂ = 3I₃
(b) I₁ = 4I₂ = 3I₃
(c) 2I₁ = I₂ = 3I₃
(d) I₁ = I₂ = I₃
Or
iv. Find the current in each resistance. (1 mark)
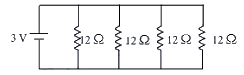(a) 1 A
(b) 2 A
(c) 3 A
(d) 0.25 A

Ans:
i. (c) The equivalent resistance in the parallel combination is lesser than the least value of the individual resistance.
ii. (b) Resistance of each piece = 12 / 4 = 3Ω
1 / Rp = 1 / 4 + 1 / 4 + 1 / 4 + 1 / 4 ⇒ Rp = 4 / 3 Ω
iii. (a) All three resistors are in parallel.
1 / Rp = 1 / 4 + 1 / 3 + 1 / 6
∴ Rp = 6 / 9 = 2 / 3 Ω
iv. (a) Voltage is the same across each resistance.
So, I₁ × 5 = I₂ × 10 = 15 × I₃
I₁ = 2I₂ = 3I₃
Or
iv. (d) All are in parallel.
1 / Rp = 1 / 12 + 1 / 12 + 1 / 12 ⇒ Rp = 3 Ω
So, current in each resistor:
I' = 3 / 12 = 1 / 4 A